

甘肃省武威市凉州区武威二十一中联片教研2023-2024学年七年级下学期7月期末数学试题
展开一.选择题(共30分)
1.(3分)如图,直线a∥b,∠A=80°,∠1=70°,则∠2的度数是( )
A.30°B.40°C.50°D.60°
2.(3分)如图是某机械加工厂加工的一种零件的示意图,其中AB∥CD,DE⊥BC,∠ABC=70°,则∠EDC等于( )
A.10°B.20°C.30°D.40°
3.(3分)下列各数中,无理数是( )
A.B.3.14C.0D.π
4.(3分)如图,数轴上表示的点是( )
A.点AB.点BC.点CD.点D
5.(3分)若将点A(1,3)向下平移4个单位,再向左平移2个单位得到点B,则点B的坐标为( )
A.(﹣3,1)B.(3,7)C.(﹣1,﹣1)D.(5,5)
6.(3分)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,1),(﹣1,2),(0,2),(1,2),(2,3),(1,3),(0,3),…,根据这个规律探索可得第2024个点的坐标是( )
A.(43,45)B.(44,45)C.(﹣43,45)D.(﹣42,45)
7.(3分)某果农将采摘的荔枝分装为大箱和小箱销售,其中每个大箱装4千克荔枝,每个小箱装3千克荔枝.该果农现采摘有32千克荔枝,根据市场销售需求,大小箱都要装满,则所装的箱数最多为( )
A.8箱B.9箱C.10箱D.11箱
8.(3分)明代《算法统宗》有一首饮酒数学诗:“醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醇酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人:薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为( )
A. B. C. D.
9.(3分)一个不等式的解在数轴上表示如图,则这个不等式可以是( )
A.x+2>0B.x﹣2<0C.2x≥4D.4﹣2x<0
10.(3分)为了了解某区初中毕业年级体育考试情况,从20000名初三年级学生中随机抽取1200名学生的体育考试成绩进行分析,下列说法正确的是( )
A.该调查方式是普查 B.每名初三学生的体育考试成绩是个体
C.1200名学生是总体的一个样本 D.20000名考生是总体
二.填空题(共24分)
11.(3分)点P在△PAB平面内一动点,∠APB=90°,AB=6,点M是PB上一点,且BM=PA,连接AM,则AM的最小值为 .
12.(3分)如图,直线CD,EF被射线OA,OB所截,CD∥EF,若∠1=105°,则∠2的度数为 .
13.(3分)若m,n为实数,且(m+4)2+=0,则(m+n)2的值为 .
14.(3分)化简:= .
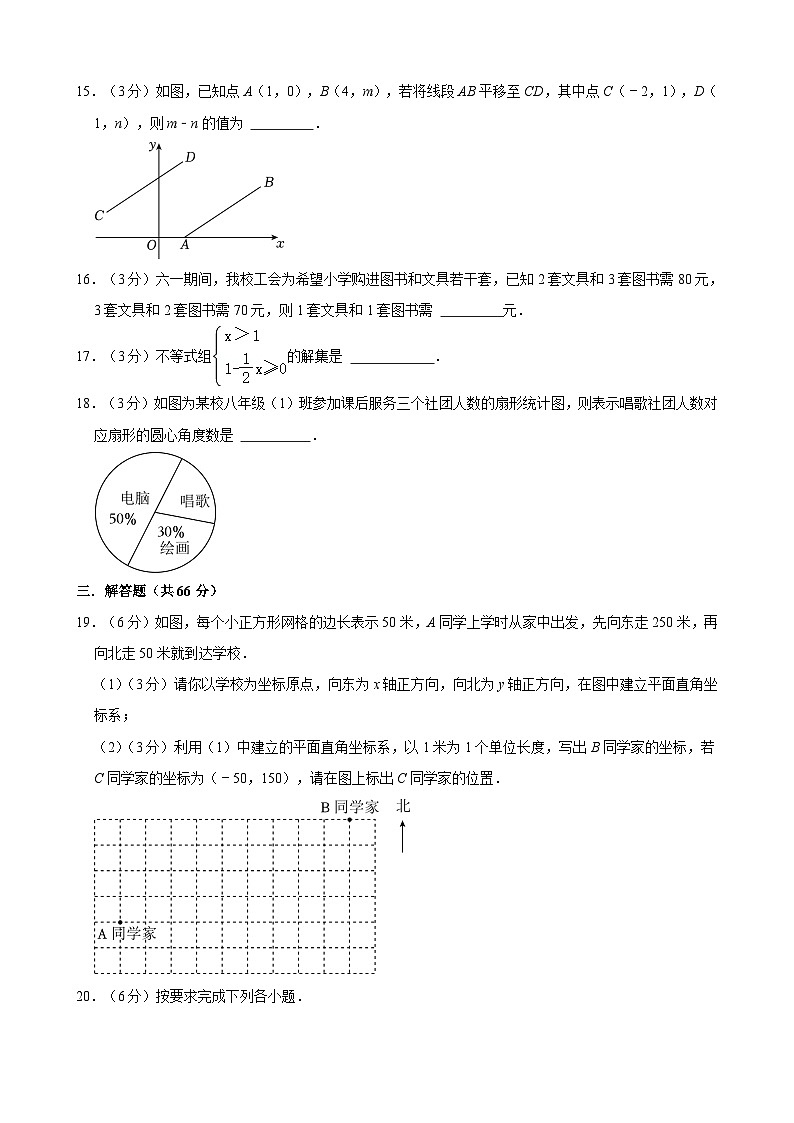
15.(3分)如图,已知点A(1,0),B(4,m),若将线段AB平移至CD,其中点C(﹣2,1),D(1,n),则m﹣n的值为 .
16.(3分)六一期间,我校工会为希望小学购进图书和文具若干套,已知2套文具和3套图书需80元,3套文具和2套图书需70元,则1套文具和1套图书需 元.
17.(3分)不等式组的解集是 .
18.(3分)如图为某校八年级(1)班参加课后服务三个社团人数的扇形统计图,则表示唱歌社团人数对应扇形的圆心角度数是 .
三.解答题(共66分)
19.(6分)如图,每个小正方形网格的边长表示50米,A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)(3分)请你以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)(3分)利用(1)中建立的平面直角坐标系,以1米为1个单位长度,写出B同学家的坐标,若C同学家的坐标为(﹣50,150),请在图上标出C同学家的位置.
20.(6分)按要求完成下列各小题.
(1)(3分)计算:;
(2)(3分)求x的值:(x+4)3=﹣64.
21.(4分)解不等式组:.
22.(6分)如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠2=55°,求∠1,∠3,∠BOE的度数.
23.(6分)如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,连接BD,DF,EF,BD和EF相交于点G,∠BGF+∠BDA=180°,AB∥DF,试说明∠BEF=∠CDF.
24.(8分)已知点A(2+a,﹣3a﹣4),解答下列各题:
(1)(4分)若点A在y轴上,求出点A的坐标;
(2)(4分)若点B的坐标为(8,5),且AB∥x轴,求出点A的坐标.
25.(6分)某校组织去井冈山开展研学旅行活动.在此次活动中,小明、小亮等同学随家长一同到某游乐园游玩.已知成人票每张35元,学生票按成人票五折优惠.他们一共12人,门票共需350元.
(1)(3分)小明他们一共去了几个成人,几个学生?
(2)(3分)如果团体票(16人或16人以上)按成人票六折优惠,请你帮助小明算一算,用哪种方式购票更省钱?
26.(6分)某合作社着力发展乡村水果网络销售,在水果收获的季节,该合作社用17500元从农户处购进A,B两种水果共1500kg进行销售,其中A种水果收购单价10元/kg,B种水果收购单价15元/kg.
(1)(3分)求A,B两种水果各购进多少千克;
(2)(3分)已知A种水果运输和仓储过程中质量损失4%,若合作社计划A种水果至少要获得20%的利润,不计其他费用,求A种水果的最低销售单价.
27.(8分)和平社区进行“远离火灾,珍爱生命,共建平安家园”宣传活动,为了了解本次活动的效果,社区抽取部分市民进行了调查,根据调查结果绘制了如图所示两幅不完整的统计图,其中A:“不了解”,B:“了解一些”,C:“基本了解”,D:“非常了解”.
(1)(2分)本次共调查了 人,D组所在扇形的圆心角的大小是 °;
(2)(2分)补全条形统计图;
(3)(2分)若该社区共5000人,估计该社区对消防知识“不了解”的人数;
(4)(2分)“安全无小事”,根据这次调查结果,说说你的看法或对该社区工作的建议.
28.(10分)已知EF∥GH,A和B分别是直线EF和GH上的点,C是这两条直线之间的一点.
(1)(3分)如图1,①已知∠CAE+∠CBG=110°,那么∠ACB= .
②在①的条件下,作∠CAE与∠CBG的平分线AD与BD相交于点D,求∠ADB的度数.
(2)(3分)如图2,作∠CAF与∠CBH的平分线AD与BD相交于点D,若∠ACB=α,求∠ADB的度数(用含α的代数式表示),并证明你的结论.
(3(4分))如图3,作∠CAE的平分线与∠CBH的平分线所在的直线AD与BD相交于点D,若∠ACB=α,请直接写出∠ADB的度数(用含α的代数式表示).
答案
1-5 ABDCC 6-10 CCABB
11. 12.75° 13.1 14.5 15.﹣1 16.30 17.1<x≤2 18.72°
19.(1)如图所示:学校位置即为所求;
(2)如图所示:B同学家的坐标为(4,3),
C同学家的位置即为所求.
20.(1)9.5. (2)x=﹣8.
21.不等式组的解集为﹣1≤x<2.
22.∵AB⊥CD,
∴∠BOC=90°,
∴∠1=∠BOC﹣∠2=90°﹣55°=35°,
∵∠3=∠1=35°,
∴∠BOE=180°﹣∠3=180°﹣35°=145°.
23.因为∠BGF=∠EGD,∠BGF+∠BDA=180°,
所以∠EGD+∠BDA=180°,
所以EF∥AC,
所以∠A=∠BEF,
因为AB∥DF,
所以∠A=∠CDF,
所以∠BEF=∠CDF.
24.(1)∵点A在y轴上,
∴2+a=0,
∴a=﹣2,
∴﹣3a﹣4=2,
∴点A的坐标为(0,2);
(2)∵点B的坐标为(8,5),且AB∥x轴,
∴﹣3a﹣4=5,
∴a=﹣3,
∴2+a=﹣1,
∴点A的坐标为(﹣1,5).
25.(1)设成人有x人,学生有y人,
由题意得:,
解得:,
答:小明他们一共去了8个成人,4个学生;
(2)如果按团体票购买共需费用:
35×0.6×16=336(元),
∵336<350,
∴购买团体票更省钱.
26.(1)设A种水果购进x千克,B种水果购进y千克,
根据题意得:,
解得:.
答:A种水果购进1000千克,B种水果购进500千克;
(2)设A种水果的销售单价为m元/千克,
根据题意得:1000×(1﹣4%)m﹣10×1000≥10×1000×20%,
解得:m≥12.5,
∴m的最小值为12.5.
答:A种水果的最低销售单价为12.5元/千克.
27.(1)20÷10%=200,
∴本次共调查了200人,
∴D组的人数为200﹣20﹣60﹣80=40人,
∴D组所在扇形的圆心角的大小是,
(2)补图如下:
;
(3)5000×10%=500,
∴对消防知识“不了解”的人数为500人;
(4)利用社区文化活动,体育活动,进行安全知识竞赛宣传,特别要各多组织一些“以人为本,安全第一”为主题的社区活动.如:“安全生产进社区”活动、“安全生产进家庭”活动等等.
28.(1)①作CP∥EF,如图所示,
∵EF∥GH,CP∥EF
∴CP∥GH,∠CAE=∠ACP,
∴∠CBG=∠BCP,
∴∠ACB=∠ACP+∠BCP=∠CAE+∠CBG,
∵∠CAE+∠CBG=110°,
∴∠ACB=110°,
故答案为:110°;
②作DQ∥EF,如图所示,
∵AD与BD分别是∠CAE与∠CBG的平分线,
∴∠DAE=∠CAE,∠DBG=∠CBG,
∴∠DAE+∠DBG=(∠CAE+∠CBG)=55°,
同①的方法可得:∠ADB=∠DAE+∠DBG=55°;
(2)∠ADB=180°−α,证明如下:
∵AD与BD分别平分∠CAF与∠CBH,
∴∠DAF=∠CAF,∠DBH=∠CBH,
∴∠DAF+∠DBH=(∠CAF+∠CBH),
由(1)①的方法可得:∠ACB=∠CAE+∠CBG,∠ADB=∠DAF+∠DBH,
∵∠ACB=α,
∴∠ACB=∠CAE+∠CBG=α,
∴∠CAF+∠CBH=(180°−∠CAE)+(180°−∠CBG)=360°−(∠CAE+∠CBG)=360°−α
∴∠ADB=(∠CAF+∠CBH)=(360°−α)=180°−α,
(3)作DM∥EF,如图所示,
∵EF∥GH,DM∥EF
∴DM∥GH,∠MDA=∠EAN,
∴∠MDB=∠DBH,
∴∠ADB=∠MDB−∠MDN=∠DBH−∠EAN,
∵AD与BD分别是∠CAE与∠CBH的平分线,
∴∠EAN=∠CAE,∠DBH=∠CBH
∴∠ADB=(∠CBH−∠CAE)
由(1)①得:∠ACB=∠CAE+∠CBG,
∵∠ACB=α,
∴∠CAE=α−∠CBG,
∴∠ADB=(∠CBH−∠CAE)=(∠CBH−α+∠CBG),
∵∠CBH+∠CBG=180°,
∴∠ADB=(180°−α)=90°−α
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2024/6/17 14:51:13;用户:15095635659;邮箱:15095635659;学号:43002344
2024年甘肃省武威市凉州区凉州区金塔中学联片教研三模数学试题: 这是一份2024年甘肃省武威市凉州区凉州区金塔中学联片教研三模数学试题,共13页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。
2024年甘肃省武威市凉州区凉州区黄羊中学联片教研三模数学试题: 这是一份2024年甘肃省武威市凉州区凉州区黄羊中学联片教研三模数学试题,共12页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。
2024年甘肃省武威市凉州区武威三中教研联片中考二模数学试题: 这是一份2024年甘肃省武威市凉州区武威三中教研联片中考二模数学试题,共9页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。












