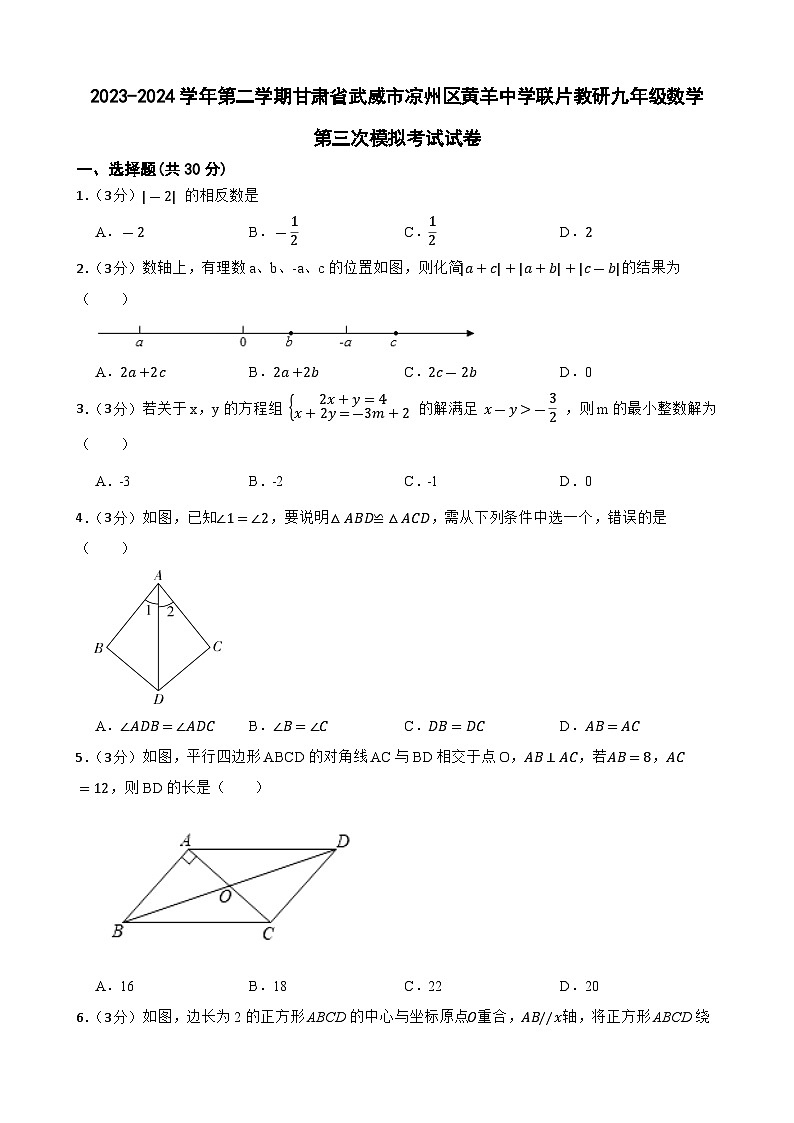
2024年甘肃省武威市凉州区凉州区黄羊中学联片教研三模数学试题

这是一份2024年甘肃省武威市凉州区凉州区黄羊中学联片教研三模数学试题，共12页。试卷主要包含了选择题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。

一、选择题(共30分)
1．（3分）|-2| 的相反数是
A．-2B．-12C．12D．2
2．（3分）数轴上，有理数a、b、-a、c的位置如图，则化简|a+c|+|a+b|+|c-b|的结果为（ ）
A．2a+2cB．2a+2bC．2c-2bD．0
3．（3分）若关于x，y的方程组 2x+y=4x+2y=-3m+2 的解满足 x-y>-32 ，则m的最小整数解为（ ）
A．﹣3B．﹣2C．﹣1D．0
4．（3分）如图，已知∠1=∠2，要说明△ABD≌△ACD，需从下列条件中选一个，错误的是（ ）
A．∠ADB=∠ADCB．∠B=∠CC．DB=DCD．AB=AC
5．（3分）如图，平行四边形ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=8，AC=12，则BD的长是（ ）
A．16B．18C．22D．20
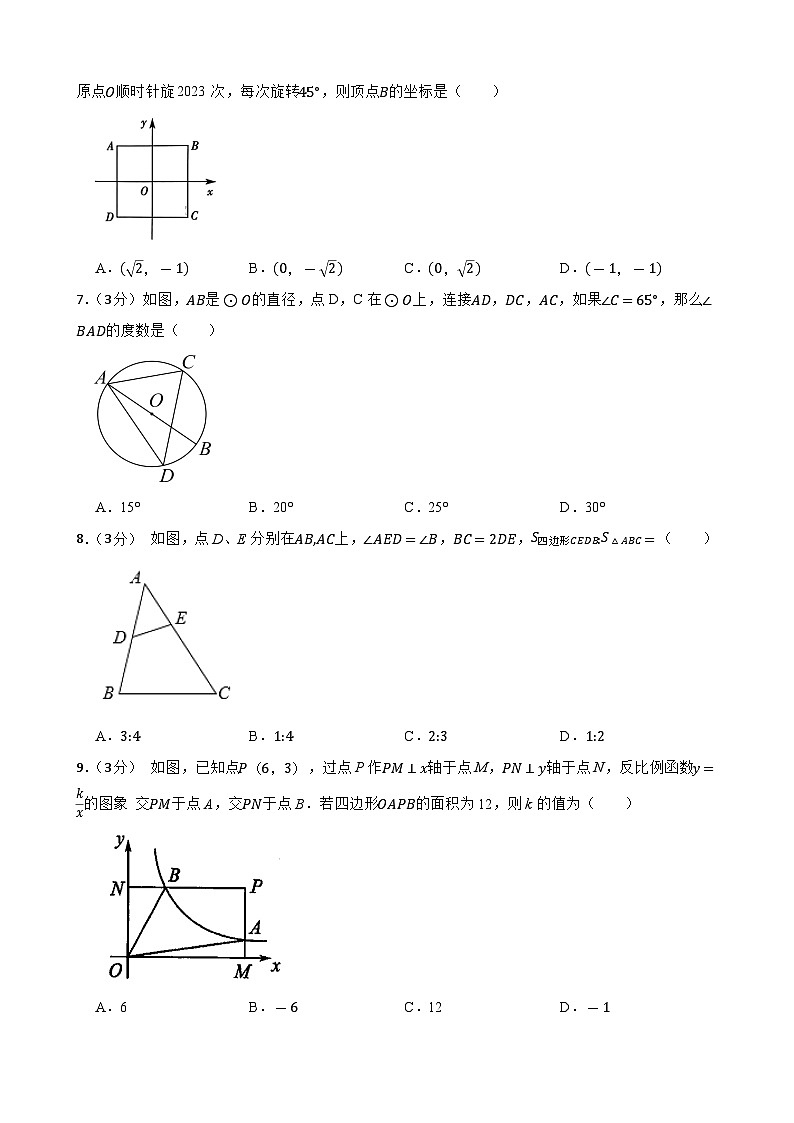
6．（3分）如图，边长为2的正方形ABCD的中心与坐标原点O重合，AB//x轴，将正方形ABCD绕原点O顺时针旋2023次，每次旋转45°，则顶点B的坐标是（ ）
A．(2，-1)B．(0，-2)C．(0，2)D．(-1，-1)
7．（3分）如图，AB是⊙O的直径，点D，C在⊙O上，连接AD，DC，AC，如果∠C=65°，那么∠BAD的度数是（ ）
A．15°B．20°C．25°D．30°
8．（3分） 如图，点D、E分别在AB,AC上，∠AED=∠B，BC=2DE，S四边形CEDB:S△ABC=（ ）
A．3:4B．1:4C．2:3D．1:2
9．（3分） 如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数y=kx的图象 交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k的值为（ ）
A．6B．-6C．12D．-1
10．（3分）如图，在矩形ABCD中，ABA．4B．3C．2D．1
二、填空题(共24分)
11．（3分）(-3)2 = ．
12．（3分）一个多边形的内角和是外角和的2倍，则这个多边形的边数为 ．
13．（3分） 如图，在▱ABCD中，AC是对角线，∠ACD=90°，E是BC的中点，AF平分∠BAC，连接CF，EF．若CF⊥AF，AB=5，BC=13，则EF的长为 ．
14．（3分）如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，将△ABC以B为中心逆时针方向旋转，得到△BDE，当点C的对应点E落在边AB上时，线段AD的长度值是 ．
15．（3分）如图，在⊙O中，AB是直径，CD⊥AB，∠ACD＝60°，OD=2，那么DC的长等于 .
16．（3分） 如图，点D、E是△ABC边BC、AC 上的点，BD:CD=2:5，连接AD、BE，交点为F，DF:AF=1:4，那么CEAE的值是 ．
17．（3分）如图，将圆形纸片折叠使弧AB经过圆心O，过点O作半径OC⊥AB于点E，点P为圆上一点，则∠APC的度数为 ．
18．（3分）如图，从三个不同方向看同一个几何体得到的平面图形，则这个几何体的侧面积是 cm2．
三、计算题(共8分)
19．（8分）计算：
（1）（4分）计算：-3+(12)-1+π+10-tan60°；
（2）（4分）先化简，再求值：(2xx-3+3xx+3)÷x2x2-9，其中x=3．
四、作图题(共4分)
20．（4分）如图，△ABC在平面直角坐标系内，顶点坐标分别为A(-1,2)，B(-3,3)，C(-3,1)．
（1）（2分）画出△ABC关于原点O成中心对称的△A1B1C1；
（2）（2分）以A为位似中心，在网格中画出△ADE，使△ADE与△ABC位似且面积比为4：1。
五、解答题(共54分)
21．（6分）已知：如图，点D在△ABC的BC边上，AC∥BE，BC=BE，∠ABC=∠E，求证：AB=DE．
22．（6分）如图，在四边形ABCD中，AB∥CD，过点D作∠ADC的角平分线交AB于点E，连接AC交DE于点O，AD∥CE．
（1）（3分）求证：四边形AECD是菱形；
（2）（3分）若AD=10，△ACD的周长为36，求菱形AECD的面积．
23．（8分）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D是AC延长线上一点，连接BD，交⊙O于点E，点F在BD上，∠DCF=∠ABC．
（1）（4分）试判断直线CF与⊙O的位置关系，并证明你的结论；
（2）（4分）若BE=CE，ACBC=34，BD=5，求⊙O的半径．
24．（8分）为了加强中小学学生的劳动教育，2024年计划将该区1000m2的土地作为社会实践基地，该基地准备种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位：元/m2）与其种植面积x（单位：m2）的函数关系y=120x+10，其中200≤x≤600；乙种蔬菜的种植成本为50元/m2．
（1）（4分）设2024年甲乙两种蔬菜总种植成本为w元，如何分配两种蔬菜的种植面积，使w最小？
（2）（4分）学校计划今后每年在这1000m2土地上，均按（1）中方案种植蔬菜，因技术改进，预计种植成本逐年下降．若甲种蔬菜种植成本平均每年下降10%，乙种蔬菜种植成本平均每年下降a%，当a为何值时，2026年的总种植成本为28920元？
25．（8分）如图，在Rt△ACB中，AC=BC，点D是AB上任意一点，连接CD，将CD绕着点C逆时针旋转90°，点D的对应点是点E，连接BE，DE．
（1）（4分）求∠ABE的度数．
（2）（4分）在旋转过程中，如果AD=3，CD=5，求BD的值．
26．（8分）如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为点E，连结AC，AD．
（1）（4分）求证：∠C＝∠BAD．
（2）（4分）若∠C＝30°，OC＝3，求AB的长度．
27．（10分）如图，在平面直角坐标系中，抛物线y=ax2+bx+3交y轴于点A，且过点B(-1，2)，C(3，0)．
（1）（3分）求抛物线的函数解析式；
（2）（3分）将抛物线向左平移m(m>0)个单位，当抛物线经过点B时，求m的值；
（3）（4分）若P是抛物线上位于第一象限内的一点，且S△ABC=2S△ACP，求点P的坐标．
答案
1-5 ACBCD 6-10 CCAAC
11．9 12．6 13．72 14．10 15．23 16．78 17．30° 18．36
19．（1）3 （2）5-3.
20．（1）如图，△A1B1C1即为所求作的三角形；
（2）如图，△AD1E1与△AD2E2即为所求作的三角形．
21．∵BE∥AC，
∴∠C=∠DBE．
在△ABC和△DEB中，
∠C=∠DBEBC=EB∠ABC=∠E ，
∴△ABC≌△DEB，
∴AB=DE．
22．（1）∵AB∥CD ，AD∥E ，
∴四边形AECD 为平行四边形，
∵AB∥CD ，
∴∠AED=∠CDE ，
∵DE 平分∠ADC ，
∴∠ADE=∠CDE ，
∴∠AED=∠ADE ，
∴AD=AE ，
∴四边形AECD 是菱形．
（2）如图，∵四边形AECD 是菱形，
∴AC⊥DE ，OD=OE ，OA=OC ，AD=CD=10 ，
∵△ACD 的周长为36，
∴AC=C△ACD-AD-CD=36-10-10=16 ，
即OA=OC=8 ．
在Rt△AOD 中，∠AOD=90° ，由勾股定理得，
∴DO2+AO2=AD2 ，即DO2=102-82 ，
∴DO=6 ．
∴DE=12 ．
∴S菱形AECD=12AC⋅DE=12×12×16=96 ．
23．（1）直线CF与⊙O相切，
证明：如图，连接OC．
∵AB是⊙O的直径，∴∠ACB=90°．
∵点D是AC延长线上一点，
∴∠DCB=90°，∴∠DCF+∠BCF=90°．
∵OC=OB，∴∠OCB=∠OBC．
∵∠DCF=∠ABC，∴∠DCF=∠OCB，
∴∠OCB+∠BCF=90°，∴∠OCF=90°，∴OC⊥CF．
∵OC是⊙O的半径，∴直线CF与⊙O相切．
（2）如图，连接AE．
∵BE=CE，∴∠BAE=∠DAE．
∵AB是⊙O的直径，∴∠AEB=∠AED=90°．
∵AE=AE，∴△AEB≌△AED(ASA)，∴AB=AD
在Rt△ACB中，ACBC=34，
设AC=3x，BC=4x，则AB=AC2+BC2=(3x)2+(4x)2=5x，
∴AD=AB=5x，DC=AD-AC=5x-3x=2x，
∴在Rt△DCB中，CD2+BC2=BD2，即(2x)2+(4x)2=(5)2，解得：x=12，
∴AB=5x=52，∴⊙O的半径为54
24．（1）当200≤x≤600时，
w=x(120x+10)+50(100-x)=120(x-400)2+42000
∵120>0，
∴抛物线开口向上．
∴当x=400时，w有最小值，w最小值=42000．
∴1000-x=1000-400=600，
∴当甲种蔬菜的种植面积为400m2，乙种蔬菜的种植面积为600m2时，w最小．
（2）由题意可知：甲、乙两种蔬菜总种植成本是42000元，
乙种蔬菜的种植成本是50×600=30000（元），
甲种蔬菜的种植成本是42000-30000=12000（元），
(1-10%)2×12000+(1-a%)2×30000=28920，
设a%=m，则(1-m)2=0.64，
解得：m1=0.2，m2=1.8（舍去），
∴a%=20%．
∴a=20．
答：当a为20时，2026年的总种植成本为28920元．
25．（1）根据旋转的性质可知：CD=CE，∠DCE=90°
∵∠ACB=∠DEC=90°
∴∠ACD=∠BCE
又∵CA=CB，CD=CE
∴△ACD≌△BCE
∴∠CAD=∠CBE
又∵∠ACB=90°，CA=CB
∴∠BAC=∠ABC=45°
∴∠ABE=∠ABC+∠CBE=90°
（2）∵△ACD≌△BCE，AD=3
∴BE=AD=3
∵CD=CE=5，∠DCE=90°
∴DE=2CD=52
在Rt△DBE中：
BD=DE2-BE2=41
26．（1）∵CD⊥AB，CD是直径，
∴AD⌢=BD⌢，
∴∠ACD=∠BAD.
（2）如图，连接OA，OB，BC，
∵CD⊥AB，CD是直径，
∴AD⌢=BD⌢，
∴CA=CB，
∴∠ACD=∠BCD=30°，
∴∠ACB=60°，
∴∠AOB=2∠ACB=120°，
∴AB⌢=nπr180=120π×3180=2π.
27．（1）把点B(-1，2)，C(3，0)代入抛物线，得
a-b+3=29a+3b+3=0
解得：a=-12，b=12
∴y=-12x2+12x+3
（2）∵y=-12x2+12x+3=-12(x-12)2+258
∴当抛物线向左平移m个单位时，y=-12(x-12+m)2+258
把B(-1，2)代入得：-12(-1-12+m)2+258=2，
解得：m1=0（舍），m2=3
∴m=3．
（3）如图：
过点P作PE⊥x轴，交AC于点E
∵A（0，3），B（-1，2），C(3，0)，
∵AB=2，AC=32，BC=25
∵AB2+AC2=BC2，
∴∠BAC=90°，
∴S△ABC=12×2×32=3
∵A（0，3），C(3，0)，
∴直线AC解析式：y=-x+3
设P(t，-12t2+12t+3)，则E(t，-t+3)
∴PE=-12t2+32t，
∴S△ACP=12×3×(-12t2+32t)=-34t2+94t
∵S△ABC=2S△ACP，
∴2(-34t2+94t)=3，
解得：t1=1，t2=2
∴P1(1，3)，P2(2，2)