初中数学北师大版（2024）七年级上册3 一元一次方程的应用课文课件ppt

这是一份初中数学北师大版（2024）七年级上册3 一元一次方程的应用课文课件ppt，共19页。PPT课件主要包含了学习目标，课堂导入，x-3400，x-100，y+100，y+3400，随堂练习等内容，欢迎下载使用。

1.能通过分析“盈不足”问题情境中的数量关系，引入适当的未知数列一元一次方程，进而解决实际问题.2.能借助列表格等方法直观分析复杂实际问题中的数量关系.
问题《九章算术》“盈不足”章第五题:今有共买金，人出四百，盈三千四百;人出三百，盈一百.问:人数、金价各几何?题目大意:几个人合伙买金，每人出400钱，会多出3 400钱;每人出300钱，会多出100钱.合伙人数、金价各是多少?
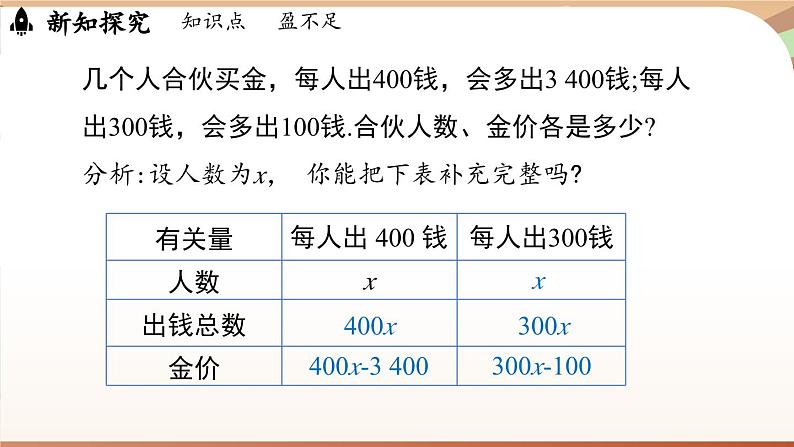
几个人合伙买金，每人出400钱，会多出3 400钱;每人出300钱，会多出100钱.合伙人数、金价各是多少?分析:设人数为x， 你能把下表补充完整吗?
解:设合伙人数为x，则金价可表示为(400x-3 400)钱，还可表示为(300x-100)钱，根据等量关系，列出方程:400x-3 400=300x-100.解这个方程，得 x=33.300×33-100=9 800.因此，人数为 33，金价为9 800钱.
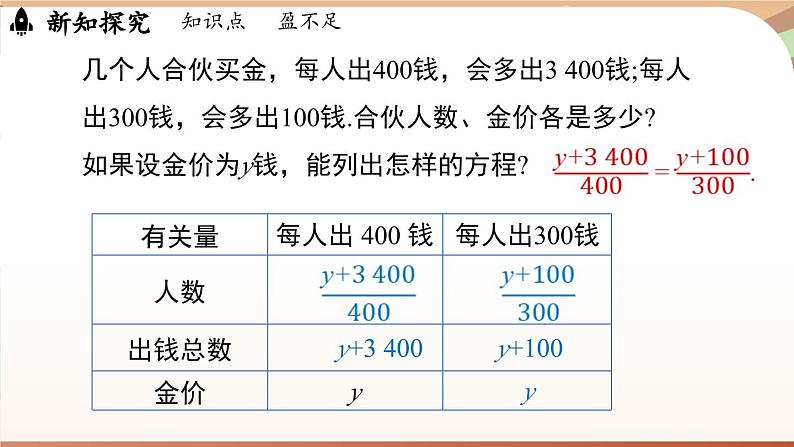
几个人合伙买金，每人出400钱，会多出3 400钱;每人出300钱，会多出100钱.合伙人数、金价各是多少?如果设金价为y钱，能列出怎样的方程?
归纳：固定数量的人去买固定物价的物品：若每人多出钱，则出钱总数相对物价就会多(即“盈”);若每人少出钱，则出钱总数相对物价就会少(即“不足”).
等量关系(物品总价相等)：每人出的钱数（多）×人数-盈数=每人出的钱数（少）×人数+不足数也可以根据人数相等找等量关系
例1 有若干人共同出钱买鸡，如果每人出九文钱，那么多了十一文钱，如果每人出六文钱，那么少了十六文钱.问共有几个人?
解:设共有x个人.根据等量关系，得9x-11=6x+16，解得 x=9.答:共有9个人.
把一些图书分给某班学生阅读，如果每人分3本，则剩余20 本;如果每人分4本，则还缺 25 本，这个班有多少名学生?
把固定数量的物品平均分给固定数量的对象
等量关系：物品总数相等/对象数相等
把一些图书分给某班学生阅读，如果每人分3本，则剩余20 本;如果每人分4本，则还缺 25 本，这个班有多少名学生? 分析:设这个班有x名学生.
解:设这个班有x名学生.根据等量关系，得3x+20=4x-25，解得x=45.答:这个班有 45 名学生.
归纳：把固定数量的物品平均分给固定数量的对象，若每对象少分一些，则物品就有余(即“盈”);若每对象多分一些，则物品就不够(即“不足”).
等量关系(物品总数相等 )：每对象分的数量（少）×对象数量+盈数=每对象分的数量（多）×对象数量-不足数也可以根据对象数相等找等量关系
解:设这个工厂有x名工人.依题意，得2x+20=3x-30.解得x=50.所以2×50+20=120(个)答:这个工厂有50名工人，有120个苹果.
例2 某工厂给工人发苹果，如果每人分2个，则剩余20个;如果每人分3个，则还缺30个，这个工厂有多少名工人?有多少个苹果?
1.某校七(1)班学生去大兴区参加训练，活动时小组组长将若干瓶矿泉水分给小组成员(包括组长).如果每人2瓶，那么剩余4瓶；如果每人3瓶，那么有一人只有1瓶，求这个小组人数及矿泉水的瓶数.
解:设这个小组有x人.根据题意，得2x+4=3(x-1)+1.解得x=6.所以矿泉水有2×6+4=16(瓶).答:这个小组有6人，有16瓶矿泉水.
2.某小组计划做一批“中国结”，如果每人做6个，那么比计划多了8个;如果每人做5个，那么比计划少了2个.小组成员共有多少名?他们计划做多少个“中国结”?
解:设小组成员共有x名，依题意，得6x-8=5x+2.解得x=10.所以6×10-8=52(个).答:小组成员共有10名，他们计划做52个“中国结”.
3. 有一群鸽子和一些鸽笼，如果每个鸽笼住6只鸽子，则剩余3只鸽子无鸽笼可住，如果再买来5只鸽子，连同原来的鸽子，每个刚好住8只.问原来有多少只鸽子，多少个鸽笼?
解:设原来有x个鸽笼.依题意，得6x+3+5=8x.解得x=4.所以6×4+3=27(只).答:原来有27只鸽子，4个鸽笼.
4. 学校分配学生住宿，如果每个房间住8人，则少12个床位;如果每个房间住9人，则空出两个房间.求房间的个数和学生的人数.
解:设有x个房间.由题意，得8x+12=9(x-2).解得x=30.所以8×30+12=252(人).答:有房间30个，学生252人.