初中数学1.5 三角形全等的判定集体备课课件ppt

这是一份初中数学1.5 三角形全等的判定集体备课课件ppt，共24页。PPT课件主要包含了知识回顾，3cm，知识点，角角边AAS，角平分线的性质，∴FMFH，∴FGFH，∴FGFM等内容，欢迎下载使用。
1．探索并理解“角角边”判定方法；2．会用“角角边”判定方法证明三角形全等；3．掌握角平分线的性质定理，能用角平分线的性质定理解决问题．
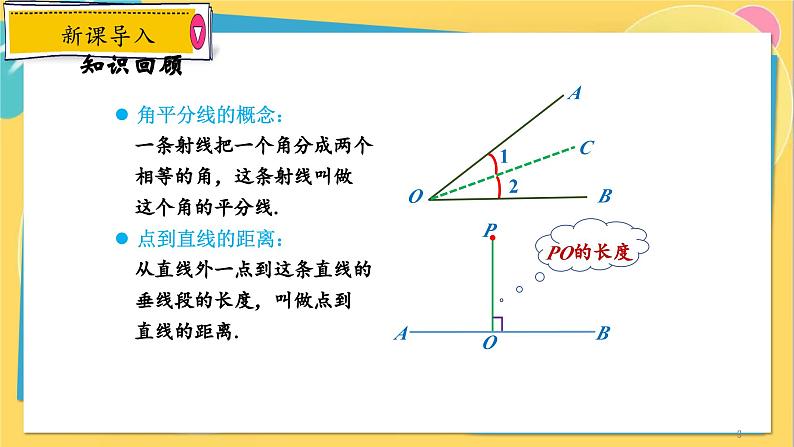
角平分线的概念： 一条射线把一个角分成两个 相等的角，这条射线叫做 这个角的平分线.点到直线的距离： 从直线外一点到这条直线的 垂线段的长度，叫做点到 直线的距离.
三角形全等的判定方法： 1.三边对应相等的两个三角形全等， 简写为“边边边”或“SSS”. 2.两边及其夹角对应相等的两个三角形全等， 简写为“边角边”或“SAS”. 3.两角及其夹边对应相等的两个三角形全等， 简写成“角边角”或“ASA”.
1.三个角.2.三条边.3.两边一角.4.两角一边
当两个三角形满足六个条件中的三个时，有四种情况:
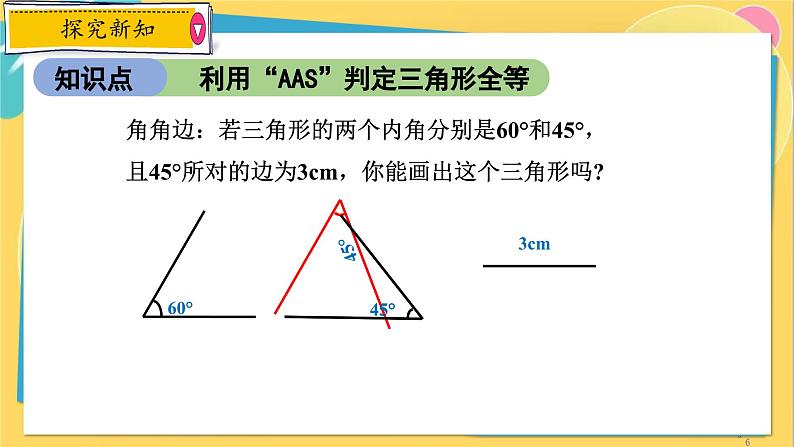
角角边：若三角形的两个内角分别是60°和45°，且45°所对的边为3cm，你能画出这个三角形吗?
利用“AAS”判定三角形全等
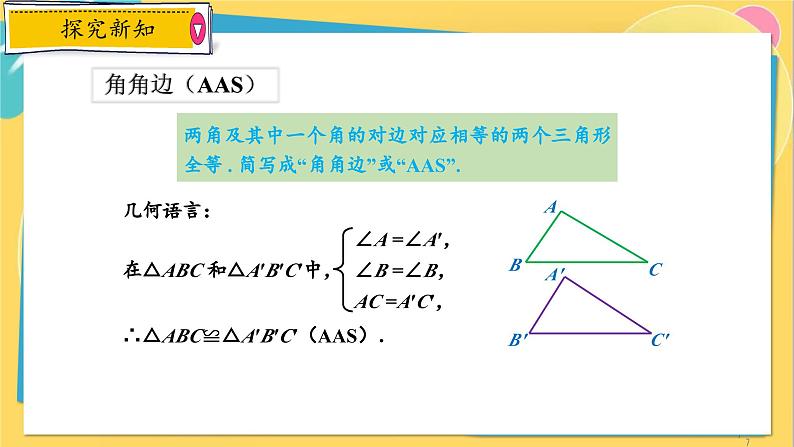
两角及其中一个角的对边对应相等的两个三角形全等 . 简写成“角角边”或“AAS”.
几何语言：在△ABC 和△A′B′C′中，∴△ABC≌△A′B′C′（AAS）．
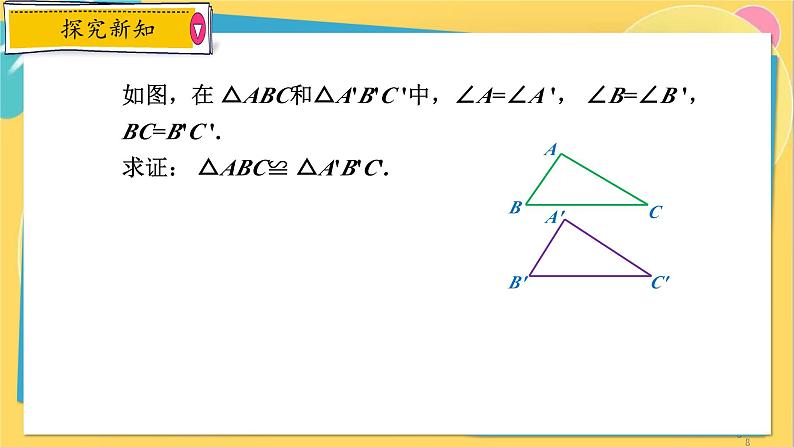
如图，在 △ABC和△A'B'C '中，∠A=∠A '， ∠B=∠B '， BC=B'C '.求证： △ABC≌ △A'B'C'.
如图，已知点E、C在线段BF上， BE=FC， ∠A=∠D，∠ACB=∠F.求证： △ABC≌△DEF
证明 ：∵ BE=FC， ∴ BE+EC=CF+EC，即BC=EF. 在△ABC和△DEF中 ∴△ABC≌△DEF（AAS）.
变式：如图，E，F 在线段AC上，AD∥CB，AE =CF．若∠B =∠D，求证：DF =BE．
证明：∵AD∥CB ，∴∠A =∠C.∵AE =CF ，∴AE-EF =CF-EF，即AF =CE.
∴△ADF ≌△CBE(AAS)．∴DF =BE(全等三角形对应边相等)．
在△ADF 和△CBE 中,
已知：如图，P是∠BAC的平分线上的一点，PB⊥AB于点B，PC⊥AC于点C. 求证：PB=PC.
你能总结出角平分线的性质吗？
角平分线上的点到角两边的距离相等.
几何语言：∵OC是∠AOB的平分线， 且PD⊥OA，PE⊥OB，∴PD=PE.
已知：如图 ，AB// CD，PB 和PC分别平分∠ABC 和∠DCB. AD过点P，且与AB 垂直.求证：PA=PD.
【分析 】由 AB∥CD，AD⊥AB，可得 AD⊥CD，则 PA，PD 的长分别是点P到AB，CD 的距离．根据角平分线的性质定理知，它们与点 P到BC的距高相等.因此，可先作出点 P到BC的垂线段.
证明 ：如图 ，作PE⊥BC 于点E.∵AB//CD(己知)，∴∠BAD＋∠CDA=180°(两直线平行，同旁内角互补)，∵AD⊥AB(已知)，∴∠BAD=90°(垂直的定义).∴∠CDA=180°－∠BAD=180°—90°=90°.∴AD⊥CD(垂直的定义). ∵PB平分∠ABC(已知)，∴PA＝PE(角平分线上的，点到角两边的距离相等).同理，PD=PE.∴PA=PE=PD.
如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，BD=2CD，点D到AB的距离为5.6cm，求BC的长.
解：过点D作DE⊥AB于点E.∵∠C=90°，AD平分∠CAB(已知)，∴CD=DE=5.6cm.(角平分线上的点到角两边的距离相等)∴BD=2CD=2×5.6=11.2(cm).∴BC=CD+BD=5.6+11.2=16.8(cm).
如图，已知：△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证：点F在∠DAE的平分线上．
又∵点F在∠CBD平分线上， 　　　　 FH⊥AD， FM⊥BC.
∴点F在∠DAE的平分线上.　　　
证明：过点F作FG⊥AE于G，FH⊥AD于H，FM⊥BC于M，
∵点F在∠BCE的平分线上， FG⊥AE， FM⊥BC，
1. 如图，点 A 在 DE 上，点 F 在 AB 上，且 AC ＝ CE ，∠1＝ ∠2，∠ B ＝∠ D ，则 DE 的长为(　C　)
2. [新考向 知识情境化]如图，已知∠ AOB ，使第一把长方形 直尺的一边与射线 OB 重合，再使第二把宽为1 cm的长方 形直尺的一边与射线 OA 重合，顶点 P 恰好落在第一把长 方形直尺的另一条边上，若射线 OP 就是∠ AOB 的平分 线，则第一把直尺的宽是(　A　)
3. [2024·杭州期中]如图， AD 是△ ABC 中∠ BAC 的平分 线， DE ⊥ AB ，交 AB 于点 E ， DF ⊥ AC ，交 AC 于点 F ，若 DE ＝2， AC ＝4，则△ ADC 的面积是(　A　)