数学八年级上册14.1.1 同底数幂的乘法教学设计

这是一份数学八年级上册14.1.1 同底数幂的乘法教学设计，共4页。教案主要包含了情境引入，教学建议，对应训练，随堂训练，课堂总结，知识结构，作业布置等内容，欢迎下载使用。

14．1.1 同底数幂的乘法
解题大招一 同底数幂的乘法性质的逆用
例1 已知am＝3，an＝21，求am＋n的值．
分析：把am＋n变成am·an，代入求值即可．
解：因为am＝3，an＝21，所以am＋n＝am·an＝3×21＝63.
解题大招二 运用同底数幂的乘法，求待定字母或式子的值
将等式两边化为同底数幂的形式，底数相同，那么指数也相同，可求出相应字母或式子的值．
例2 若82a＋3·8b－2＝810，求2a＋b的值．
分析：根据同底数幂相乘，底数不变，指数相加，可得a，b的关系，再根据a，b的关系求解．
解：因为82a＋3·8b－2＝82a＋3＋b－2＝810，所以2a＋3＋b－2＝10，所以2a＋b＝9.
解题大招三 同底数幂的混合运算
先确定底数(有些需要变形化为同底数)，再进行同底数幂的乘法运算，最后算整式的加减．
例3 计算：(1)32×312－311×27；
(2)(－x)3·x5－x·x3·(－x)4；
(3)(m－1)2·(m－1)3＋(m－1)4·(1－m)．
解：(1)原式＝314－311×33＝314－314＝0；
(2)原式＝－x3·x5－x·x3·x4＝－x8－x8＝－2x8；
(3)原式＝(m－1)5－(m－1)4·(m－1)＝(m－1)5－(m－1)5＝0.
培优点 利用同底数幂的乘法探究指数的关系
例 已知2a＝8，2b＝4，2c＝32，则a，b，c之间有怎样的关系？请说明理由．
分析：观察题目可以发现8×4＝32，利用同底数幂相乘，将等式两边转化为底数相同的形式，利用底数不变，指数相加来解答．
解：a＋b＝c.理由：因为2a·2b＝2a＋b＝8×4＝32＝2c，所以a＋b＝c.
教学目标
课题
14.1.1 同底数幂的乘法
授课人
素养目标
1.理解同底数幂的乘法的性质，能正确地运用性质解决一些简单问题.
2.会用数学的思维推导“同底数幂的乘法的性质”，使学生初步理解从特殊到一般，再由一般到特殊的认知规律.
3.通过对公式的应用，进一步发展学生观察、归纳、类比等能力，发展有条理的思考能力和表达能力的同时，体会学习数学的兴趣，培养学习数学的信心.
教学重点
正确理解同底数幂的乘法的性质．
教学难点
同底数幂的乘法的性质的灵活运用.
教学活动
教学步骤
师生活动
活动一：创设情境，复习导入
设计意图
让学生回顾乘方的相关知识，为同底数幂的乘法的学习做铺垫.
【情境引入】
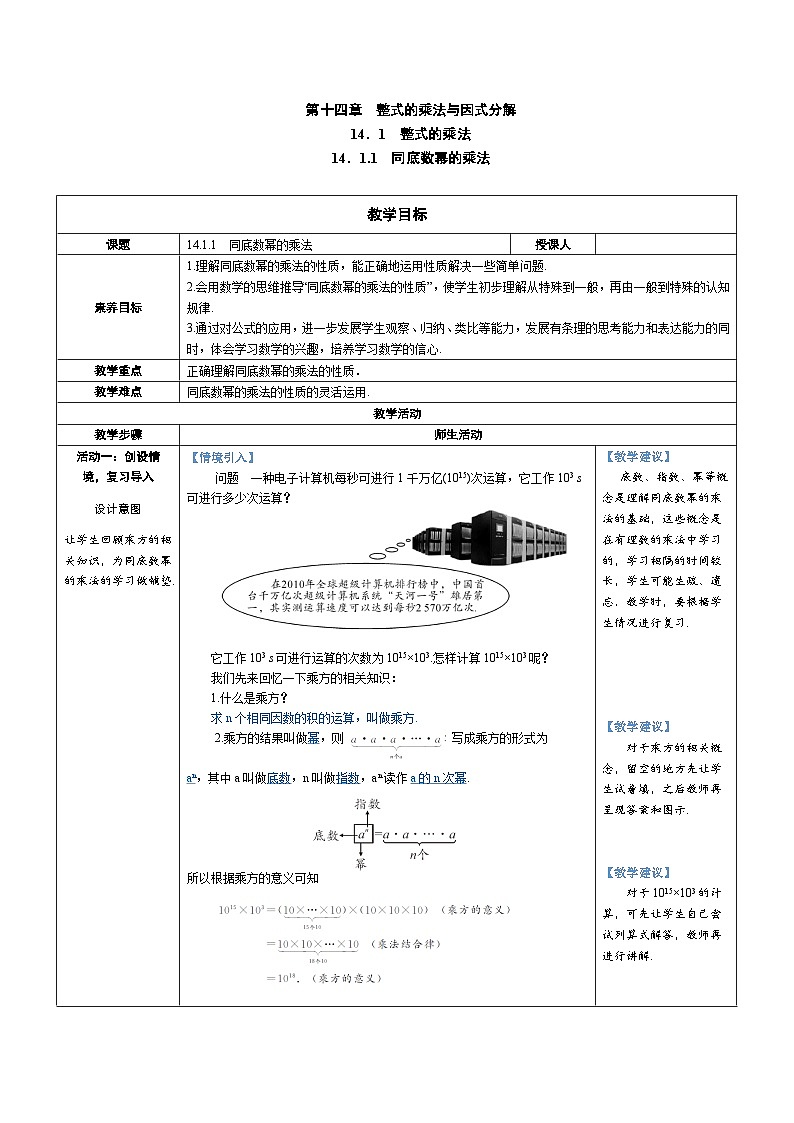
问题 一种电子计算机每秒可进行1千万亿(1015)次运算，它工作103 s可进行多少次运算？
它工作103 s可进行运算的次数为1015×103.怎样计算1015×103呢？
我们先来回忆一下乘方的相关知识：
1.什么是乘方？
求n个相同因数的积的运算，叫做乘方.
2.乘方的结果叫做幂，则 eq^\(a·a·a·…·a,\s\d4(n个a))写成乘方的形式为
an，其中a叫做底数，n叫做指数，an读作a的n次幂.
所以根据乘方的意义可知
【教学建议】
底数、指数、幂等概念是理解同底数幂的乘法的基础，这些概念是在有理数的乘法中学习的，学习相隔的时间较长，学生可能生疏、遗忘．教学时，要根据学生情况进行复习.
【教学建议】
对于乘方的相关概念，留空的地方先让学生试着填，之后教师再呈现答案和图示.
【教学建议】
对于1015×103的计算，可先让学生自己尝试列算式解答，教师再进行讲解.
教学步骤
师生活动
活动二：实践探究，获取新知
设计意图
由于学生对用字母表示幂的指数还是首次遇到，所以采用这种从1015×103和25×22到a3·a2，再从a3·a2到am·an，把幂的底数与指数分两步进行抽象，帮助学生理解，再用例题和习题巩固该性质.探究点同底数幂的乘法的性质
接下来，请同学们根据乘方的意义，完成下列填空.
(1)25×22=(2×2×2×2×2)×(2×2)=2×2×2×2×2×2×2=27；
(2)a3·a2=(a·a·a)·(a·a)=a·a·a·a·a=a5；
思考：①上述三个乘法运算式子的乘数有什么共同特征吗？
乘数均为同底数的幂.
②通过上述三个算式的计算规律，你能计算am·an吗？
公式引入
因此，我们有am·an=am+n(m,n都是正整数).
即同底数幂相乘，底数不变，指数相加.
例 (教材P96例1)计算：
(1)x2·x5；
(2)a·a6；
(3)(－2)×(－2)4×(－2)3；
(4)xm·x3m＋1.
解：(1)x2·x5＝x2＋5＝x7；
(2)a·a6＝a1＋6＝a7；
(3)(－2)×(－2)4×(－2)3＝(－2)1＋4＋3＝(－2)8＝256；
(4)xm·x3m＋1＝xm＋3m＋1＝x4m＋1.
【对应训练】
教材P96练习．
【教学建议】
1.教学时，教师要明白这三个特殊的算式具有代表性和层次性，第1个式子的底数和指数都是数；第2个式子的底数为字母，指数为数；第3个式子的底数为数，指数为字母．教学时要让学生体会从特殊到一般的思维过程.
2.此性质导出后，应要求学生用语言叙述这个性质，这对于提高学生数学语言的表述能力是有益的．另外还要明确，这个性质也适用于三个及以上的同底数幂相乘．即am·an·…·ap＝am＋n＋p(m，n，…，p都是正整数).
【教学建议】
教学时应着重说明底数是什么，指数是什么，让学生观察是不是同底数的幂相乘，引导学生运用性质进行计算，从而使学生进一步理解和掌握性质．另外，在讲解例题(2)时注意提醒学生a＝a1.
活动三：拓展提高，巩固升华
设计意图
补充此例题是告诉学生当底数为多项式或底数互为相反数时，该如何运用性质解题，强化学生的运算能力.
例 计算：
(1)(m＋n)3·(m＋n)4；
(2)－a3·(－a)2；
(3)(x－y)2·(y－x)5.
解：(1)(m＋n)3·(m＋n)4＝(m＋n)3＋4＝(m＋n)7；
(2)－a3·(－a)2＝－a3·a2＝－a3＋2＝－a5；
(3)(x－y)2·(y－x)5＝－(x－y)2·(x－y)5＝－(x－y)7.
【对应训练】
计算：(1)－x4·(－x)3；
(2)(m－n)3·(m－n)5·(n－m)2.
解：(1)－x4·(－x)3＝－x4·(－x3)＝x4＋3＝x7；
(2)(m－n)3·(m－n)5·(n－m)2＝(m－n)3·(m－n)5·(m－n)2＝(m－n)3＋5
【教学建议】
教师总结：若底数为同一个多项式，可将底数看成一个整体进行计算；若底数互为相反数，可考虑将它们化为同底数，可参考如下：
教学步骤
师生活动
活动四：随堂训练，课堂总结
【随堂训练】见《创优作业》“随堂小练”册子相应课时随堂训练.
【课堂总结】师生一起回顾本节课所学主要内容，并请学生回答以下问题：
1.同底数幂的乘法的性质是什么？用式子如何表示？
2.三个及以上的同底数幂相乘的性质是什么？用式子如何表示？
【知识结构】
【作业布置】
1.教材P104～105习题14.1第1(1)(2)，9题.
2.《创优作业》主体本部分相应课时训练．
板书设计
板书设计14.1 整式的乘法
14.1.1 同底数幂的乘法
文字表述：同底数幂相乘，底数不变，指数相加.
字母表示：am·an＝am＋n (m，n都是正整数).
条件：(1)同底数幂；(2)乘法． 结果：(1)底数不变；(2)指数相加．
教学反思
在整个教学过程中，把注意力集中在学生身上，充分发挥学生的互动性，激发和鼓励学生的学习探究兴趣；提问不仅有序、有提示、有鼓励、有启发，且问在有疑之处．从课堂发言和练习来看，学生在探究其性质时，推理能力和有条理的符号表达能力得到了一定发展.