初中数学鲁教版 (五四制)六年级下册3 平行线的性质精品ppt课件

这是一份初中数学鲁教版 (五四制)六年级下册3 平行线的性质精品ppt课件，共24页。PPT课件主要包含了②不共顶点的角，互为补角，∠3和∠4，∠5和∠4，∠5和∠2，在“三线八角”中，∠1和∠2，∠5和∠6，∠7和∠8，∠7和∠4等内容，欢迎下载使用。

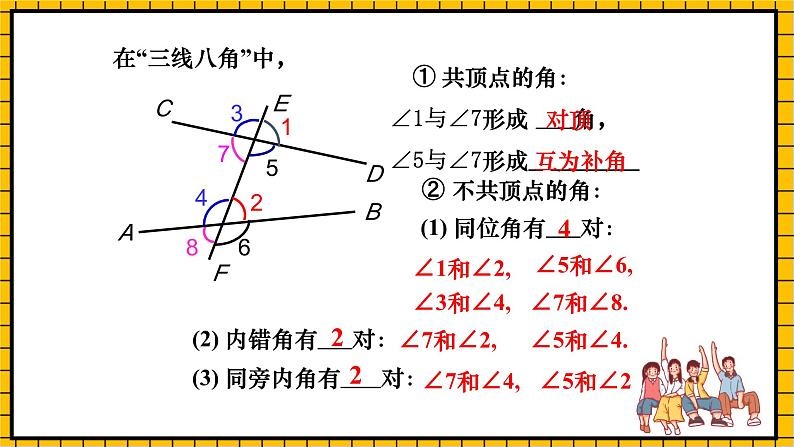
① 共顶点的角：∠1与∠7形成 角， ∠5与∠7形成
(1) 同位角有 对：
(2) 内错角有 对：
(3) 同旁内角有 对：
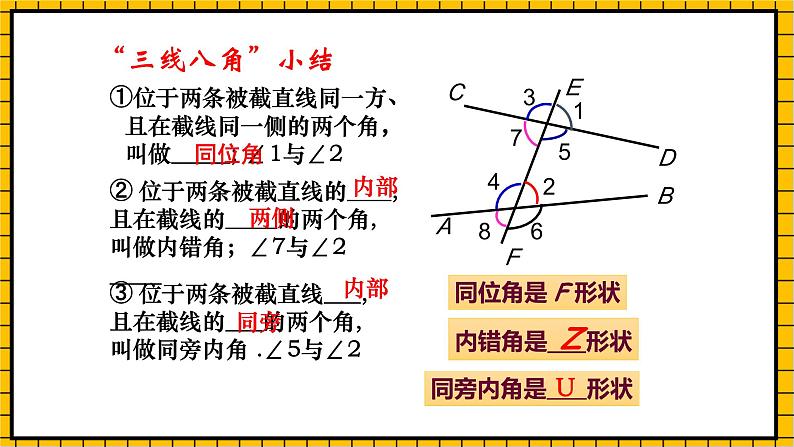
同旁内角是 形状
①位于两条被截直线同一方、
② 位于两条被截直线的 , 且在截线的 的两个角,叫做内错角；∠7与∠2
且在截线同一侧的两个角，叫做 ; ∠1与∠2
③ 位于两条被截直线 ,且在截线的 的两个角, 叫做同旁内角 .∠5与∠2
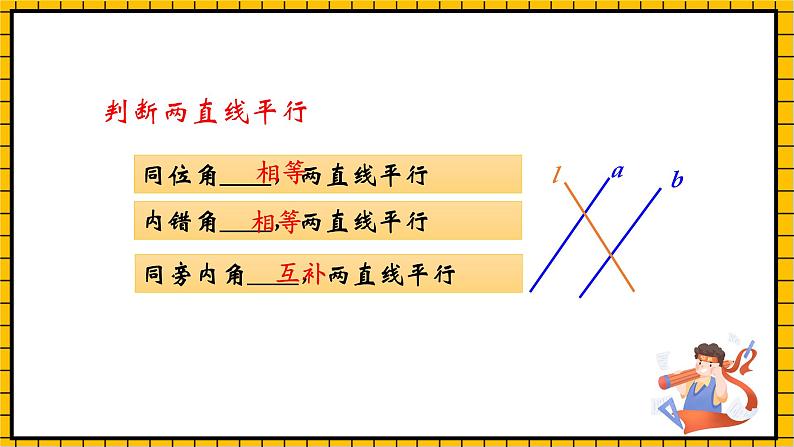
内错角 ，两直线平行
同位角 ，两直线平行
同旁内角 ，两直线平行
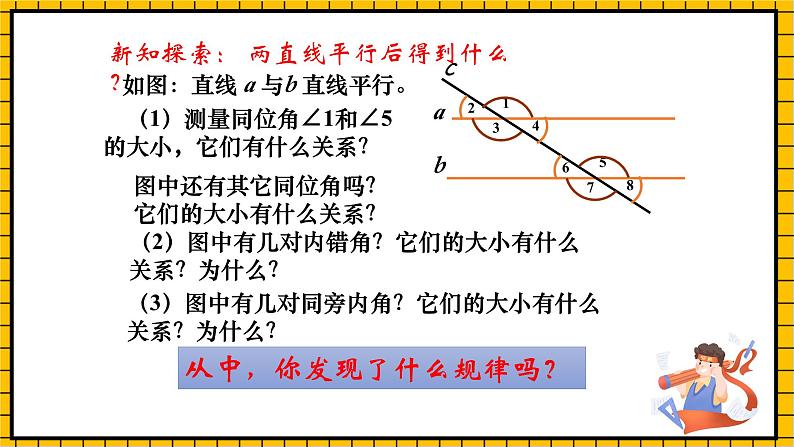
新知探索： 两直线平行后得到什么？
如图：直线 a 与b 直线平行。
（1）测量同位角∠1和∠5的大小，它们有什么关系？
图中还有其它同位角吗？它们的大小有什么关系？
（2）图中有几对内错角？它们的大小有什么关系？为什么？
（3）图中有几对同旁内角？它们的大小有什么关系？为什么？
从中，你发现了什么规律吗？
同位角相等，内错角相等，同旁内角互补。
你能根据性质1,说出性质2,性质3成立的理由吗? 已知：a∥b，求证：∠4=∠5证明：∵a∥b.（已知） ∴∠1=∠5 ( ) 又∵∠1=∠ (对顶角相等) ∴∠4=∠5（等量代换）   同样,对于性质3,你能说出道理吗?
两直线平行，同位角相等
两直线平行，内错角相等。
已知：a∥b，求证：∠3+∠5=180°
证明：∵ a ∥ b (已知) ∴∠1=∠5( )
又∵ ∠1＋∠3=180° ( )
∴ ∠3＋∠5=180°
请大家填写下面的表格，加以对比:
同位角相等 两直线平行 内错角相等 同旁内角互补
判定：角的关系 线的关系             性质：线的关系 角的关系
如图：一束平行光线AB和DE射向一个水平镜面后被反射，此时∠1=∠2 ， ∠3=∠4 。
（1 ）∠1，∠3的大小有什么关系？
（2 ）反射光线BC与EF也平行吗？
∵ ∠2=∠4 ∴ BC∥EF 。
1、如图所示，AB∥CD，AC∥BD。分别找出与∠1相等或互补的角。
如图，与∠1相等的角有：
∠3， ∠5， ∠7， ∠9， ∠11， ∠13， ∠15；
∠2， ∠4， ∠6， ∠8， ∠10， ∠12， ∠14， ∠16 ；
2.如图a∥b，c ∥d，∠１=60°,那么 ①∠2=____ ②∠3=____ ③ ∠4=____ ④ ∠5=____
3、如图，已知AG//CF，AB//CD，∠A＝40，求∠C的度数。
∵ AG//CF(已知)
(两直线平行,同位角相等)
又∵AB//CD(已知)
4、如图所示 ∠1 =∠2 求证 ： ∠3 =∠4
证明：∵ ∠1 =∠2（已知）
∴a//b(同位角相等,两直线平行)
∴ ∠3 =∠4(两直线平行，内错角相等)
5、如图，⑴如果AB//PC，∠P=35°，那么∠PAB=_____；
⑵如果AD//BC，∠2=18°， ∠5=40°，那么ABC=_____；
⑶如果AP//BD，那么∠P=∠___；
⑷如果AB//CD，那么∠ABC+ ∠C =____.
6、如图，直线AB//CD，E在AB与CD之间，且∠B=61°，∠D=34°.求∠BED的度数.
同位角相等内错角相等同旁内角互补
本节课学习了平行线的三个性质，总结了平行线的判定与性质的区别．
两直线平行同旁内角互补
∴∠D=∠α=45°(两直线平行，同位角相等)
∴∠B+∠C=180°(两直线平行，同旁内角互补)
∴∠B=180°-∠C=135°