初中数学沪科版八年级下册17.5 一元二次方程的应用完整版ppt课件

这是一份初中数学沪科版八年级下册17.5 一元二次方程的应用完整版ppt课件，文件包含沪科版数学八年级下册175《一元二次方程的应用》第2课时课件pptx、沪科版数学八年级下册175《一元二次方程的应用》第2课时教案docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

（1）能根据实际问题中的数量关系，列出一元二次方程；
（4）在经历建立方程模型解决实际问题过程中，培养提高学生分析问题的能力，体会数学建模和符号化思想，感受数学的应用价值.
（2）能根据问题的实际意义检验所得的结果是否合理；
（3）通过解决实际问题，学会将实际应用问题转化为数学问题，体会方程是刻画现实世界的一个有效的数学模型；
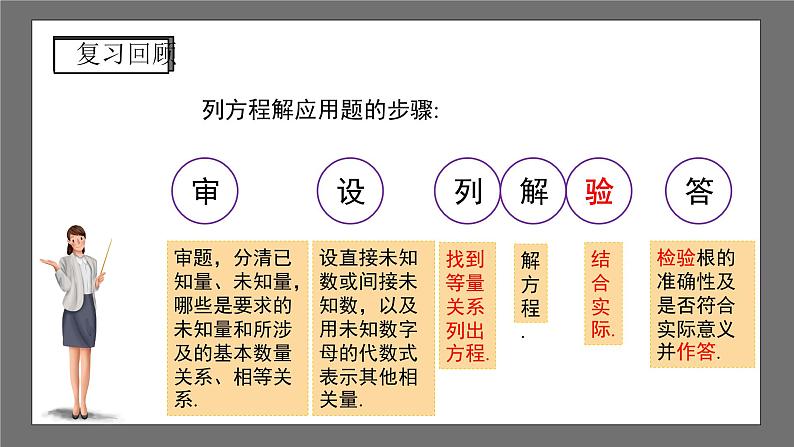
列方程解应用题的步骤:
审题，分清已知量、未知量，哪些是要求的未知量和所涉及的基本数量关系、相等关系.
设直接未知数或间接未知数，以及用未知数字母的代数式表示其他相关量.
找到等量关系列出方程.
检验根的准确性及是否符合实际意义并作答.
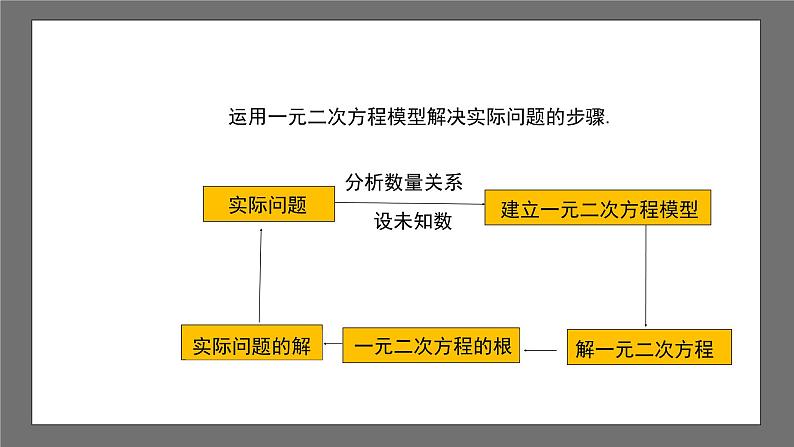
运用一元二次方程模型解决实际问题的步骤.
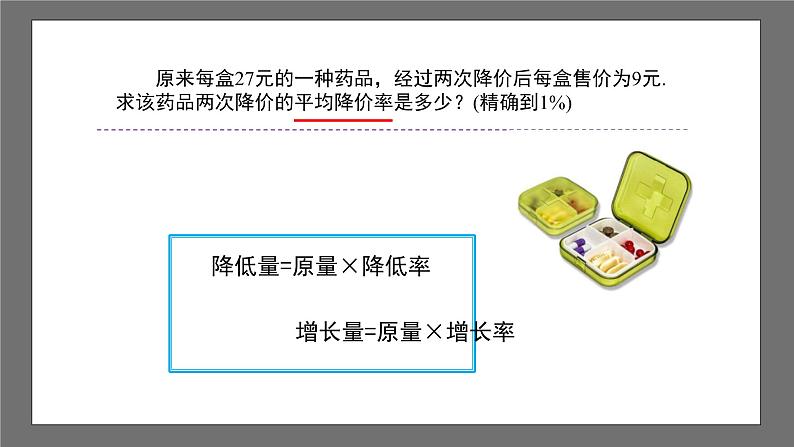
原来每盒27元的一种药品，经过两次降价后每盒售价为9元.求该药品两次降价的平均降价率是多少？(精确到1%)
问题1：未知数设什么？
该药品两次降价的平均降价率是x.
问题2：第一次降价后每盒售价多少？
问题3：第二次降价后每盒售价多少？
=27(1− x)2 元
第一次降价后的价格−第二次降低量
− 27(1− x) x
=27(1− x) 元
解：设该种药品两次平均降价率是x.
27(1− x)2 =9
答：该药品两次降价的平均降价率约是42%.
假设：原价a，降价率x.
假设：原量a，增长率t.
每公顷的产量×出油率=油量
3000(1+x)kg
新品种每公顷的产量×新品种出油率=新品种油量
解：设新品种花生产量的增长率为x，
＜0，(不合题意，舍去).
答：新品种花生产量的增长率为20%.
1. 某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某超市一月份的营业额为200万元，一月、二月、三月的营业额共1000万元，如果平均月增长率为x，则由题意得方程为( ).
200(1+x)2=1000 200+200×2×x=1000C.200+200×3×x=1000D.200+200(1+x)+ 200(1+x)2=1000
解：设该厂6月份、7月份产量的月平均增长率为x，可列方程为：
整理，得25x2+50x−11=0
解得 x1=0.2，x2= −2.2
−2.2 ＜0不合题意，舍去.
答：该厂6月份、7月份产量的月平均增长率为20%.
3.某磷肥厂去年4月份生产磷肥500 t；因管理不善，5月份的磷肥产量减少了10%；从6月份起强化了管理，产量逐月上升，7月份产量达到648 t.求该厂6月份、7月份产量的月平均增长率.
教科书第48页8题、第49页6题.