





沪科版八年级下册17.5 一元二次方程的应用优秀ppt课件
展开(1)能根据实际问题中的数量关系,列出分式方程并转化成一元二次方程;
(4)在经历建立方程模型解决实际问题过程中,培养提高学生分析问题的能力,体会数学建模和符号化思想,感受数学的应用价值.
(2)能验证分式方程的根并能根据问题的实际意义检验所得的结果是否合理;
(3)通过解决实际问题,学会将实际应用问题转化为数学问题,体会方程是刻画现实世界的一个有效的数学模型;
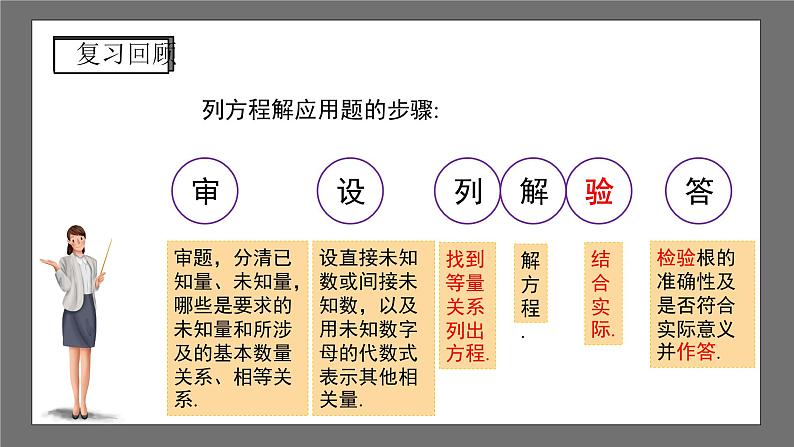
列方程解应用题的步骤:
审题,分清已知量、未知量,哪些是要求的未知量和所涉及的基本数量关系、相等关系.
设直接未知数或间接未知数,以及用未知数字母的代数式表示其他相关量.
找到等量关系列出方程.
检验根的准确性及是否符合实际意义并作答.
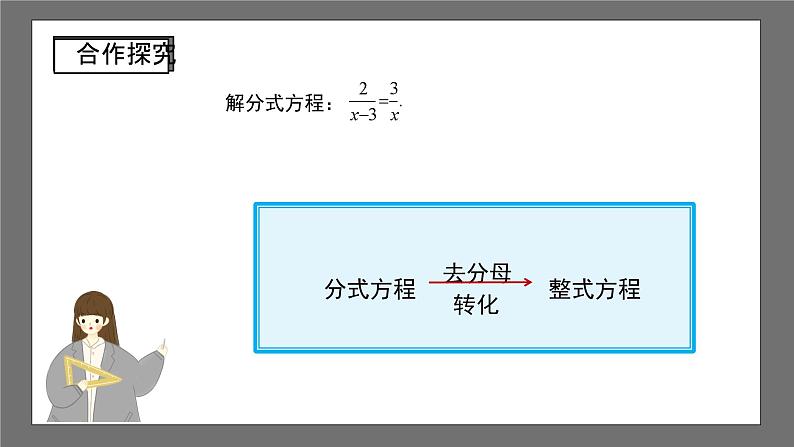
解分式方程:
解:方程两边乘各分母的最简公分母x(x – 3),得
2x =3x – 9.解得
检验:当x=9时,x(x – 3)
所以,原分式方程的解为x=9.
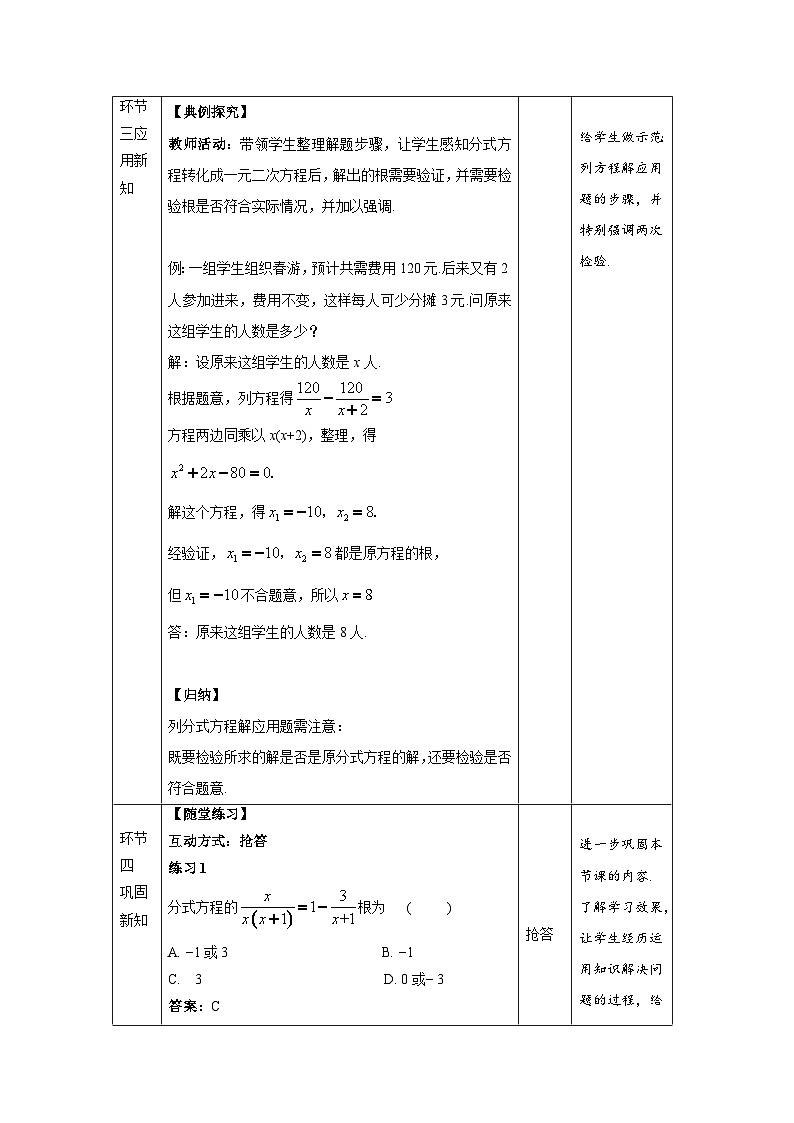
一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
问题1:题目中涉及哪些量?
总费用、每人费用、原学生人数、现学生人数.
问题2:未知数设什么?
设原来这组学生的人数是x人.
问题3:题目中有怎样的等量关系?
原来这组学生每人分摊的费用−加入后该组学生每人分摊的费用=3元
解:设原来这组学生的人数是x人.
方程两边同乘以x(x+2),整理,得
答:原来这组学生的人数是8人.
既要检验所求的解是否是原分式方程的解,还要检验是否符合题意.
1. 分式方程的 根为 ( )A. −1或3 B. −1C. 3 D. 0或− 3
2. 为了绿化荒山,某村计划在荒山上种植100棵树.原计划每天种x棵,由于邻村的支援,每天比原计划多种了40棵,结果提前5天完成了任务.则可以列出方程为( )A. B. C. D.
3.几个同学计划租车到长城旅游,应付车费480元,临行前又来了两个同学参加,这样使每人分担的车费减少8元.设这次到长城旅游的同学x个,根据题意得( )A. B. C. D.
解:设原计划每天组装x台,根据题意可列方程为:
整理,得x2+5x−150=0
解得 x1= −15, x2= 10.
经检验, x1= −15不是大于0的整数,不合题意.
答:原计划每天组装10台.
4.某空调厂的装配车间,原计划用若干天组装150台空调,厂家为了使空调提前上市,决定每天多组装3台,这样提前3天超额完成了任务,总共比原计划多组装6台,问原计划每天组装多少台?
当x=10时,符合题意.
经验证, x1= −15, x2= 10都是原方程的根,
一元二次方程的应用丨含分式
教科书第50页10题.
初中数学沪科版八年级下册17.5 一元二次方程的应用完整版ppt课件: 这是一份初中数学沪科版八年级下册<a href="/sx/tb_c70399_t3/?tag_id=26" target="_blank">17.5 一元二次方程的应用完整版ppt课件</a>,文件包含沪科版数学八年级下册175《一元二次方程的应用》第2课时课件pptx、沪科版数学八年级下册175《一元二次方程的应用》第2课时教案docx等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
数学沪科版17.5 一元二次方程的应用课文内容课件ppt: 这是一份数学沪科版<a href="/sx/tb_c70399_t3/?tag_id=26" target="_blank">17.5 一元二次方程的应用课文内容课件ppt</a>,共19页。PPT课件主要包含了整理以上方程可得,1-x,解这个方程得,%1+x,x10220%,不合题意舍去,x2-32,x+2,原来人数为,解法二等内容,欢迎下载使用。
初中数学沪科版八年级下册17.5 一元二次方程的应用说课课件ppt: 这是一份初中数学沪科版八年级下册<a href="/sx/tb_c70399_t3/?tag_id=26" target="_blank">17.5 一元二次方程的应用说课课件ppt</a>,共23页。PPT课件主要包含了面积问题,复习引入,注本题方案有无数种,∴此方程无解,补充例题与练习,化简得,x米2,如图设路宽为x米,20-x米,32-x米等内容,欢迎下载使用。













