

广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年九年级下学期月考数学试题
展开说明:1.全卷共6页,满分为120分,考试用时120分钟.
2.答卷前,考生务必用黑色字迹的签字笔或钢笔填写自己的准考证号、姓名、考场号、座位号.
3.必须用黑色字迹钢笔或签字笔作答,选择题在相应的表格中作答,非选择题在相应的答题区域作答;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生务必保持卷面的整洁.考试结束时,将试卷交回.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列实数中,最小的数为( )
A.B.1C.D.
2.2023年,广东经济延续恢复发展态势,农业生产持续向好,工业生产稳步回升,新动能加快发展,供需两端稳步改善,高质量发展稳步推进,成为全国首个地区生产总值突破13万亿元的省份,将数据“13万亿”用科学记数法表示为( )
A.B.C.D.
3.“杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取7株水稻苗,测得苗高(单位:)分别是:23,24,23,25,26,23,25.则这组数据的众数和中位数分别是( )
A.24,25B.23,24C23,23D.24,24
4.不等式组的解集在数轴上可以表示为( )
A.B.
C.D.
5.下列各式计算正确的是( )
A.B.C.D.
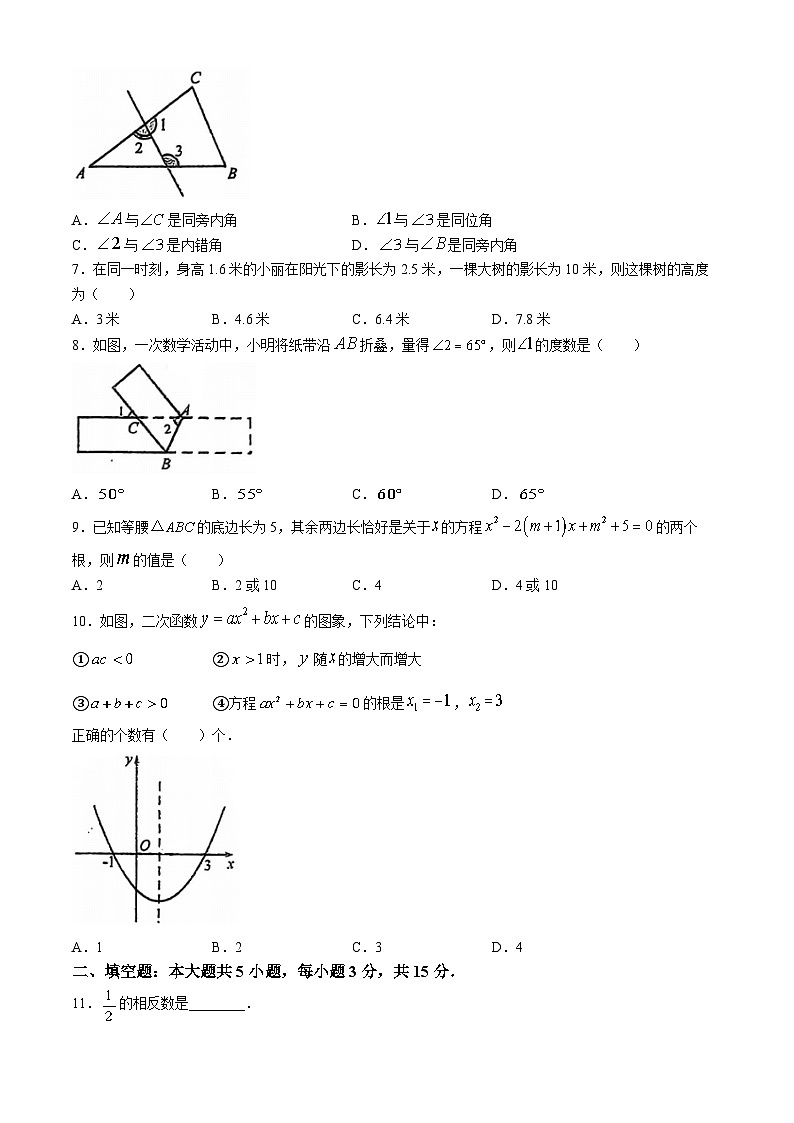
6.如图,下列说法错误的是( )
A.与是同旁内角B.与是同位角
C.与是内错角D.与是同旁内角
7.在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为10米,则这棵树的高度为( )
A.3米B.4.6米C.6.4米D.7.8米
8.如图,一次数学活动中,小明将纸带沿折叠,量得,则的度数是( )
A.B.C.D.
9.已知等腰的底边长为5,其余两边长恰好是关于的方程的两个根,则的值是( )
A.2B.2或10C.4D.4或10
10.如图,二次函数的图象,下列结论中:
①②时,随的增大而增大
③④方程的根是,
正确的个数有( )个.
A.1B.2C.3D.4
二、填空题:本大题共5小题,每小题3分,共15分.
11.的相反数是________.
12.分解因式:________.
13.一个多边形的内角和为,这个多边形是________边形.
14.已知实数,满足,则________.
15.如图,和为等腰直角三角形,,、分别交边于点、,若,5,则________.
三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.
16.(1)计算:;
(2)解分式方程:.
17.(1)实践与操作:如图,已知线段,,,用尺规作图求作:,使,,;(不写作法,保留作图痕迹)
(2)应用与计算:在(1)的条件下,,,求边的长度.
18.综合与实践:
某校“综合与实践”小组想测量塔的高度,在处仰望塔顶,测得仰角,再往塔的方向前进至处,测得仰角,并进行了计算.测量结果如下表:
请根据该表中的测量数据,计算出塔高.(参考数据:,,)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,反比例函数的图象与直线相交于点,直线与轴交于点,与轴交于点,点是的中点,点的横坐标为.
(1)求直线的函数解析式;
(2)求的面积.
20.为落实“双减”工作,打造某市中小学特色印记,某校开展多形式中小学课后服务课程,开设了.体验海天酱油制作,.咏春拳基本功学习,.醒狮文化,.剪纸鉴赏与制作,共四门课程供学生选择,每名学生只能选一门课程,每门课程被选到的机会均等,为了解学生的选课情况,该校抽取部分学生进行了调查,根据调查结果绘制了如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了________名学生,表示课程的扇形圆心角为________度,并将条形统计图补充完整;
(2)已知课程中有男生2名,女生1名,从中选出两人去参加市中学生课后服务征文比赛,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.
21.杭州亚运会的三个吉祥物“琼琼”“宸宸”“莲莲”组合名为“江南忆”,出自唐朝诗人白居易的名句“江南忆,最忆是杭州”.吉祥物一开售,就深受大家的喜爱.某商店销售这种吉祥物,每件进价60元,规定销售单价不能超过每件100元,试销售期间发现,当销售单价定为80元时,每天可售出100件,销售单价每上涨1元,每天销售量减少2件.
(1)假设每件吉祥物的销售单价上涨元,销售量为件,写出关于的函数关系式:________;
(2)每件吉祥物销售单价为多少元时,商店每天获利2450元?
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如题22-1图,已知为半圆的直径,点、、顺次排列在直径上,分别以、为一边作正方形和正方形,点、在半圆上,连接、,.
(1)当点位于半圆上时,如题22-1图,求证:;
(2)当时,如题22-2图,求的大小;
(3)在点的运动过程中,的大小是否会发生改变?请说明理由.
23.平行四边形中,是边上的动点,过点作,垂足为点,点是边的中点,连接、、.
(1)如题23-1图,当是边的中点时,________;(填“>”、“<”、“=”)
(2)如题23-2图,当点与点重合时,证明:;
(3)如题23-3图,如果,,设,,当取得最大值时,求的值.
九年级第三次适应性测试卷
数学答案
一、选择题(本大题共10小题,每小题3分,共30分)
二、填空题(本大题共5小题,每小题3分,共15分)
11.;12.;13.八;14.15;16..
三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.
16.(1)解:原式4分
5分
(2)解:整理得:,2分
解得:,4分
经检验,是原分式方程的根.5分
17.解:(1)如图所示,为所求;
4分
(2)如图,在中,,∵,,5分
∴由勾股定理可得:,7分
18.解:∵,∴,设米,
在中,,,∴,2分
在中,,,
∵,∴,4分
∵,∴,解得:米.6分
答:塔的高度约为75米.7分
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.解:(1)∵点在反比例函数上,点的横坐标是,
∴,∴,2分
∵将点代入得:,解得,4分
∴直线的函数解析式为:;5分
(2)由(1)得:,
∵点是的中点,点在轴上,点在轴上,
∴,7分
∴,8分
∴.9分
20.(1)20;144;课程的人数为:(名);3分
补全条形统计图如图所示:
4分
(2)根据题意,列表表示出所有可能出现的结果如下:
6分
①由表可知共有6种等可能的结果,7分
②其中所选两名学生恰好是1名男生和1名女生的结果有4种,即(男1,女),(男2,女),(女,男1),(女,男2),8分
③∴所选学生恰是一男一女的概率.9分
21.(1);2分
(2)解:根据题意得:,5分
整理得:,解得:,7分
∴,符合题意,8分
答:每件吉祥物销售单价为95元时,商店每天获利2450元.9分
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.解:(1)连接,1分
∵四边形是正方形,
∴,,2分
又∵,3分
∴,4分
∴;5分
(2)∵四边形、都是正方形,
∴,,,6分
∴,,7分
∴;8分
(3)方法一:设正方形和正方形的边长分别为,,
,,
在中,得,
在中,得,
∴,
解得:,9分
∴,,
又∵,
∴,10分
∴,
又∵,∴,
∴.12分
方法二:如图,延长交于点,连接、,
∵,∴,∵四边形是正方形,
∴,,∴,9分
∵四边形是正方形,∴,,∴,10分
∴,
∴点、、三点共线,11分
∵圆心角与圆周角所对的弧是弧,
∴.12分
23.(1)=2分
(2)证明:取的中点,连接与交于点,3分
∵四边形是平行四边形,∴,,
∵点、分别是,的中点,∴,
∴四边形是平行四边形,
∴,∴,∴点是中点,4分
∵,∴,
∴是的垂直平分线,5分
∴;6分
(3)过点作交延长线于点,点作交延长线于点,
∵,∴,,,
∵,∴四边形是菱形,∴,
∴,,,
∵,∴,,,8分
∴
,10分
∵是边上的动点,,∴,
∵,对称轴,
∴当时,取得最大值.12分课题
测量塔高
测量工具
测倾器,皮尺等
测量示意图
表示塔高,点、表示地面两个测绘点,、在同一直线上,,垂足为.
测量对象
的度数
的度数
的长度
测量结果
37°
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
B
C
D
B
C
A
A
C
一
二
女
男1
男2
女
(男1,女)
(男2,女)
男1
(女,男1)
(男2,男1)
男2
(女,男2)
(男1,男2)
广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年八年级下学期期中数学试题(无答案): 这是一份广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年八年级下学期期中数学试题(无答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年八年级下学期6月期中数学试题: 这是一份广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年八年级下学期6月期中数学试题,共4页。
广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年七年级上册第二次月考数学试题(含解析): 这是一份广东省佛山市南海区桂城街道灯湖初级中学2023-2024学年七年级上册第二次月考数学试题(含解析),共17页。试卷主要包含了选择题,填空题,解答题一,解答题二,解答题三;等内容,欢迎下载使用。












