考题猜想1-2 平面图形的认识（二）（压轴题，三角形的九大经典模型）（原卷版+解析版）

这是一份考题猜想1-2 平面图形的认识（二）（压轴题，三角形的九大经典模型）（原卷版+解析版），文件包含考题猜想1-2平面图形的认识二压轴题三角形的九大经典模型原卷版docx、考题猜想1-2平面图形的认识二压轴题三角形的九大经典模型解析版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

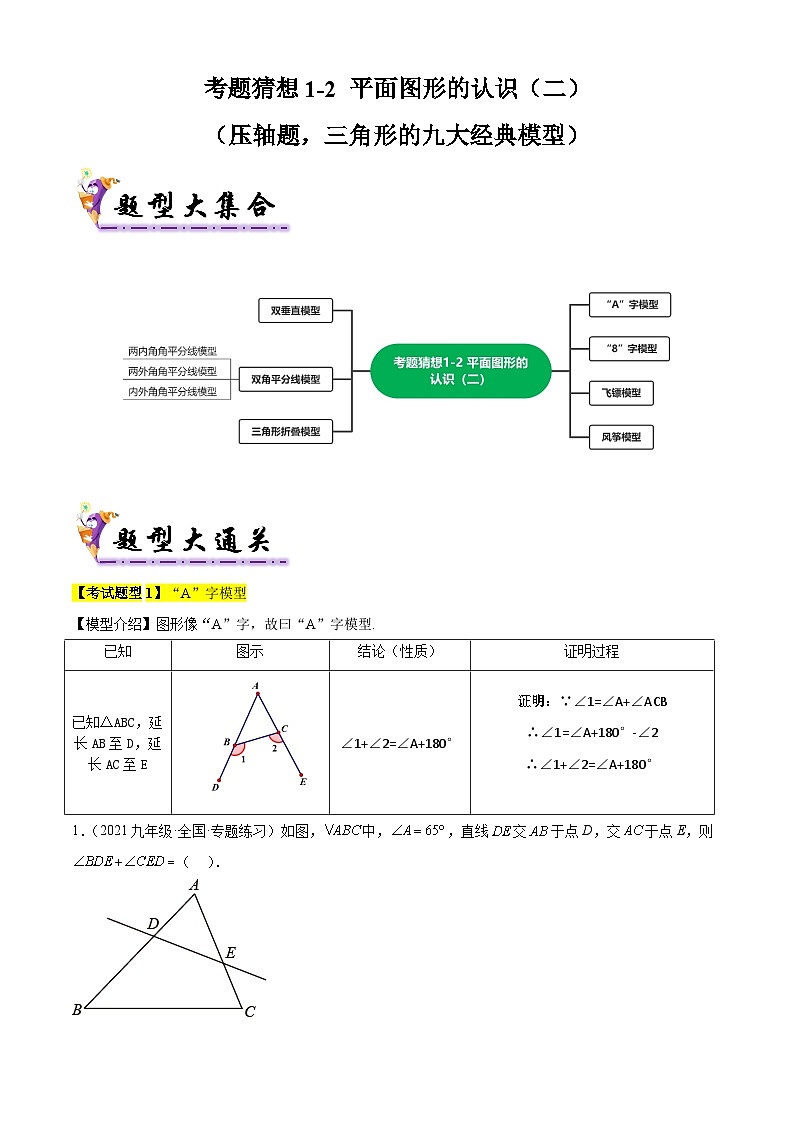
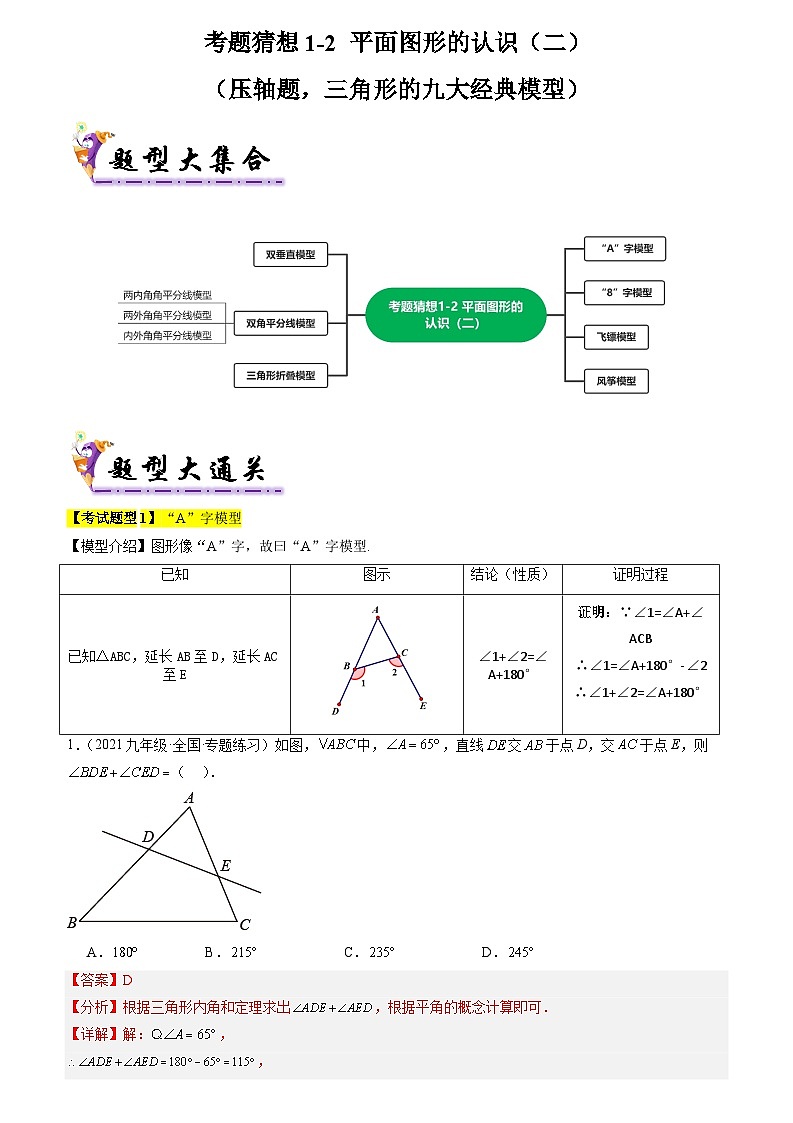
【考试题型1】“A”字模型
【模型介绍】图形像“A”字，故曰“A”字模型.
1．（2021九年级·全国·专题练习）如图，中，，直线交于点D，交于点E，则（ ）．
A．B．C．D．
2．（2021九年级·全国·专题练习）如图所示，的两边上各有一点，连接，求证．
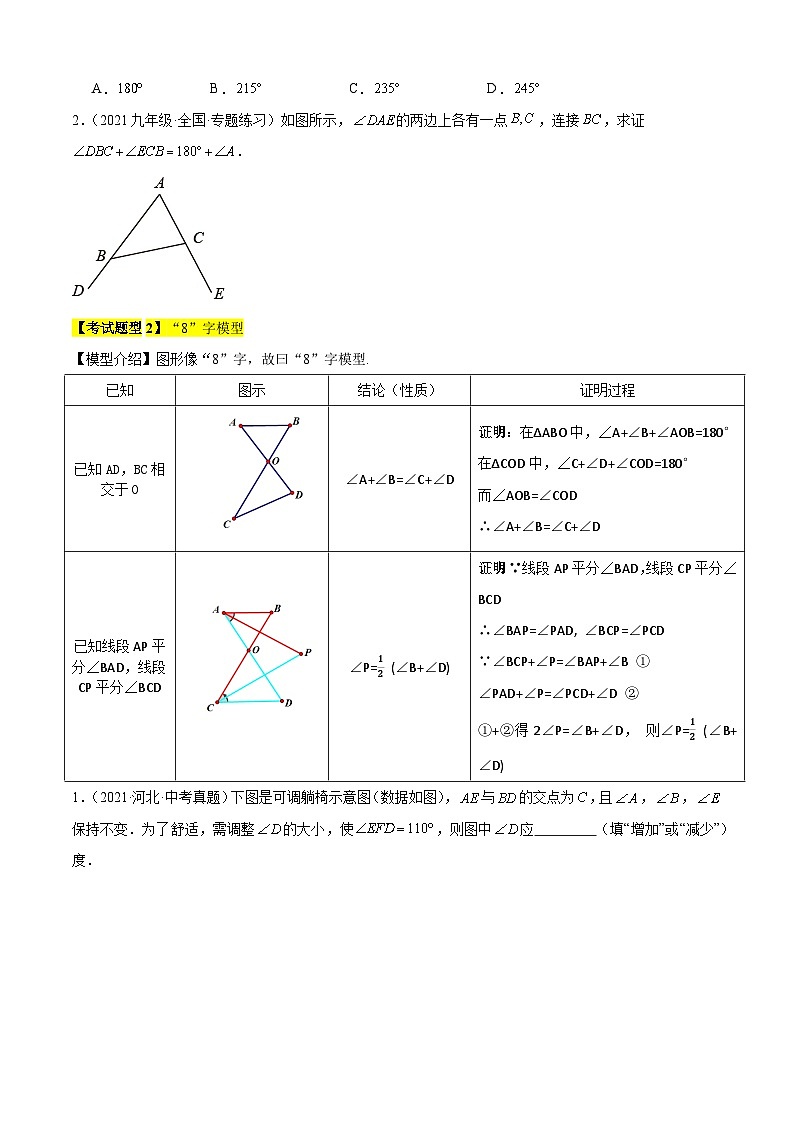
【考试题型2】“8”字模型
【模型介绍】图形像“8”字，故曰“8”字模型.
1．（2021·河北·中考真题）下图是可调躺椅示意图（数据如图），与的交点为，且，，保持不变．为了舒适，需调整的大小，使，则图中应 （填“增加”或“减少”） 度．
2．（2020九年级·全国·专题练习）阅读材料：
如图1，AB、CD交于点O，我们把△AOD和△BOC叫做对顶三角形．
结论：若△AOD和△BOC是对顶三角形，则∠A+∠D＝∠B+∠C．
结论应用举例：
如图2：求五角星的五个内角之和，即∠A+∠B+∠ACE+∠ADB+∠E的度数．
解：连接CD，由对顶三角形的性质得：∠B+∠E＝∠1+∠2，
在△ACD中，∵∠A+∠ACD+∠ADC＝180°，
即∠A+∠3+∠1+∠2+∠4＝180°，
∴∠A+∠ACE+∠B+∠E+ADB＝180°
即五角星的五个内角之和为180°．
解决问题：
（1）如图①，∠A+∠B+∠C+∠D+∠E+∠F＝ ；
（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝ ；
（3）如图③，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H＝ ；
（4）如图④，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N＝ ；
请你从图③或图④中任选一个，写出你的计算过程．
3．（23-24八年级上·江西南昌·阶段练习）北京奥运会，2008年8月8日晚上8时整在中国首都北京开幕，这或许能体现出中国人如何痴迷于幸运数字“8”，恰逢今年11月江西师大附中将迎来80周年华诞，岁经八秩，桃李芬芳，那么让我们一起来感受一下“8”的魅力．
如图1的图形我们把它称为“8字形”，显然有；
新定义：在图1中，我们把，，，叫做“8字形”的边，，，，叫做“8字形”的内角，“8字形”的一边与其相邻边的延长线组成的角叫做外角．例如，图2中，，为“8字形”的内角，图3中，，为“8字形”的外角．

(1)在图2中，的平分线和的平分线相交于点P，若，，求的度数．
(2)在图3中，的平分线和的平分线所在直线相交于点P，猜想与、的关系，并说明理由．
(3)在图4中，的平分线和的平分线相交于点P，猜想与、的关系，并说明理由．
(4)在图5中，的平分线和的平分线相交于点P，用、来表示出，直接写出结论，无需说明理由．
4．（22-23七年级下·陕西西安·期中）我们把有一组对顶角的两个三角形组成的图形叫做“8”字图形，如图1，，相交于点O，连接，得到“8”字图形．

(1)如图1，试说明的理由；
(2)如图2，和的平分线相交于点E，利用．（1）中的结论探索与、间的关系．
(3)如图3，点E为延长线上一点，分别是、的四等分线，且，，的延长线与交于点P，请探索与、的关系．
【考试题型3】飞镖模型
【模型介绍】图形像“飞镖”，故曰飞镖模型.
1．（2021九年级·全国·专题练习）如图所示，已知四边形，求证．
2．（2020九年级·全国·专题练习）如图1所示的图形，像我们常见的符号——箭号．我们不妨把这样图形叫做“箭头四角形”．
探究：
（1）观察“箭头四角形”，试探究与∠A、∠B、∠C之间的关系，并说明理由；
应用：
（2）请你直接利用以上结论，解决以下两个问题：
①如图2，把一块三角尺XYZ放置在上，使三角尺的两条直角边、恰好经过点、，若，则 ；
②如图3，、的2等分线（即角平分线）、相交于点，若，，求的度数；
拓展：
（3）如图4，，分别是、的2020等分线（），它们的交点从上到下依次为、、、…、．已知，，则 度．
3．（23-24七年级下·广东惠州·期中）将一个直角三角形纸板放置在锐角上，使该直角三角形纸板的两条直角边，分别经过点M，N．
【发现】
（1）如图1，若点A在内，当时，则 ；
（2）如图2，若点A在内，当时， ；
【探究】
若点A在内，请你判断，和之间满足怎样的数量关系，并写出理由；
【应用】
如图3，点A在内，过点P作直线，若，求的度数；
【拓展】
如图4，当点A在外，请直接写出，和之间满足的数量关系 ．
【考试题型4】风筝模型
1．（22-23七年级下·江苏南京·期中）如图，在和中，．点F与A位于线段所在直线的两侧，分别延长、至点、．

【特殊化思考】
若时，请尝试探究：
（1）当在内部时，请直接写出、与的数量关系为__________；
（2）当在外部时，请直接写出、与的数量关系为__________；
（3）若平分，平分．无论点在内部（如图③）还是外部（如图④）时，都有，请选择一幅图进行证明；

【一般化探究】
若时，请尝试探究：
（4）若射线、分别是，的等分线（为大于2的正整数），且，．当时，直接写出与需满足的条件：__________．
2．（23-24八年级上·辽宁抚顺·阶段练习）在中，，点D，E分别是边，上的两个定点，点P是平面内一动点，令，，．
初探：
（1）如图1，若点P在线段上运动，
①当时，则______；
②，，之间的数量关系为∶_______
再探：
（2）若点P运动到边的延长线上，交于F，如图2，则，，之间有何关系？并说明理由．
拓展：
（3）当点P在的内部，且D，P，E不共线时，记，，，探究，，之间的关系，并直接写出探究结论．

【考试题型5】三角形折叠模型
1．（23-24七年级下·吉林长春·期中）在中，．点D、E分别在的边上，且均不与的顶点重合，连接，将沿折叠，使点A的对称点始终落在四边形的外部，交边于点F，且点与点C在直线的异侧．
(1)如图①，则_______．
(2)如图②，则_______．
(3)如图③，设图②中的．求的度数；
(4)当的某条边与或垂直时，直接写出的度数．
2．（19-20八年级上·辽宁沈阳·期末）如图1，等边中，点D为中点，点E为边上一动点（不与点C重合），关于的轴对称图形为．

(1)如图1，当点F在上时，求证：；
(2)如图2，当点F在内部时，求的度数；
(3)如图3，当点F在外部，上方时，直接写出的度数．
3．（22-23七年级下·江苏宿迁·期中）（1）如图1，将纸片沿折叠，使点落在四边形内点的位置．则之间的数量关系为：_______；

（2）如图2，若将（1）中“点落在四边形内点的位置”变为“点落在四边形外点的位置”，则此时之间的数量关系为：_________；

（3）如图3，将四边形纸片（，与不平行）沿折叠成图3的形状，若，，求的度数；
（4）在图3中作出的平分线，试判断射线的位置关系，当点在边上向点移动时（不与点重合），的大小随之改变（其它条件不变），上述，的位置关系改变吗？为什么？
【考试题型6】双角平分线模型
【类型一】两内角角平分线模型
1．（23-24七年级下·湖南衡阳·期中）在我们华师版义务教育教科书数学七下第82页曾经研究过三角形角平分线的夹角问题．明明在研究完上面的问题后，对这类问题进行了深入的研究，他的研究过程如下：
【问题改编】
（1）如图1，在中，、的角平分线交于点P，若．则________；
【问题推广】
（2）如图2，在中，的角平分线与的外角的角平分线交于点P，过点B作于点H，若，求的度数；
（3）如图3，在中，、分别平分、，M、N、Q分别在、、的延长线上，、分别平分、，、分别平分、．若，则的度数为________（结果用含n的代数式表示）；
【拓展提升】
（4）在四边形中，，点F在直线上运动（点F不与E，D两点重合），连接，，、的角平分线交于点Q，若，，直接写出和α，β之间的数量关系．
2．（23-24七年级下·江苏南京·阶段练习）直线与直线垂直相交于，点在射线上运动，点在射线上运动．

(1)如图，已知、分别是和角的平分线，点、在运动的过程中，的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；
(2)如图，延长至，已知、的角平分线与的角平分线及其延长线相交于、，在中，如果有一个角是另一个角的倍，试求的度数．
(3)如图，延长至，已知、的等分线（、）与的等分线（）及其延长线相交于、，在中，如果有一个角是另一个角的倍，直接写出的度数．（结果可用含的代数式表示）
3．（23-24七年级下·江苏无锡·阶段练习）【概念认识】
如图①，在中，若，则，叫做的“三分线”其中，是“邻三分线”，是“邻三分线”．
【问题解决】
（1）如图①，，，是的“三分线”，则 ______ ；
（2）如图②，在中，，，若的三分线交于点，则 ______ ；
（3）如图③，在中，、分别是邻三分线和邻三分线，且，求的度数；
【延伸推广】（4）在中，是的外角，的三分线所在的直线与的三分线所在的直线交于点若，，直接写出的度数．（用含m、n的代数式表示）
4．（23-24七年级下·山东济南·阶段练习）阅读下面的材料，并解决问题．
(1)已知在中，，图1﹣图3的的内角平分线或外角平分线交于点O，请直接求出下列角度的度数．
如图1， ；
如图2， ；
如图3， ；
如图4，，的三等分线交于点，，连接，则 ．
(2)如图5，点O是△两条内角平分线的交点，则 ．
(3)如图6，中，的三等分线分别与的平分线交于点，，若，，求的度数．
【类型二】两外角角平分线模型
1．（22-23七年级下·江苏南通·期末）如图，锐角，点，分别在，上．
(1)如图，若，连接，，，的平分线与的平分线交于点，则 ______ ， ______ ；
(2)若点在内部点不在线段上，连接，，，，，分别平分和，且与交于点，求的度数；
(3)如图，点是线段延长线上一点，过点作于点，与的平分线交于点，请直接写出与的数量关系．
2．（21-22八年级上·湖北武汉·期中）已知：在中，的角平分线交于点O，的外角平分线交于点D．

(1)请探究的度数与的度数有什么数量关系？并证明你的结论．
(2)若C的三个外角平分线的交点为D、E、F，请判断是锐角三角形还是钝角三角形或直角三角形？并证明你的结论．
【类型三】内外角角平分线模型
1．（23-24八年级上·天津津南·期中）在中，
(1)如下图所示，如果，和的平分线相交于点P，那么__________；
(2)如下图所示，和的平分线相交于点P，试说明；
(3)如下图所示， 和的平分线相交于点P，猜想与的关系，直接写出答案，不用证明．
2．（20-21八年级上·河北沧州·阶段练习）∠ACD是△的外角，的平分线与的平分线交于点，的平分线与的平分线交于点，…，的平分线与的平分线交于点An． 设∠A＝．则＝ ，∠A2021＝ ．
3．（20-21八年级上·湖南长沙·阶段练习）如图，在中，、分别平分，，的延长线交外角的角平分线于点．以下结论：①；②；③；④．其中正确的结论有 （填序号）．
【考试题型7】双垂直模型
1．（20-21七年级下·安徽合肥·期末）如图1，AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．
（1）求证：∠EAB＝∠CED；
（2）如图2，AF、DF分别平分∠BAE和∠CDE，则∠F的度数是 （直接写出答案即可）；
（3）如图3，EH平分∠CED，EH的反向延长线交∠BAE的平分线AF于点G．求证：EG⊥AF．（提示：三角形内角和等于180°）
已知
图示
结论（性质）
证明过程
已知△ABC，延长AB至D，延长AC至E
∠1+∠2=∠A+180°
证明：∵∠1=∠A+∠ACB
∴∠1=∠A+180°-∠2
∴∠1+∠2=∠A+180°
已知
图示
结论（性质）
证明过程
已知AD，BC相交于O
∠A+∠B=∠C+∠D
证明：在∆ABO中，∠A+∠B+∠AOB=180°
在∆COD中，∠C+∠D+∠COD=180°
而∠AOB=∠COD
∴∠A+∠B=∠C+∠D
已知线段AP平分∠BAD，线段CP平分∠BCD
∠P=12 (∠B+∠D)
证明：∵线段AP平分∠BAD，线段CP平分∠BCD
∴∠BAP=∠PAD, ∠BCP=∠PCD
∵∠BCP+∠P=∠BAP+∠B ①
∠PAD+∠P=∠PCD+∠D ②
①+②得2∠P=∠B+∠D， 则∠P=12 (∠B+∠D)
已知
图示
结论（性质）
证明方法
已知四边形ABCD
∠C=∠A+∠B+∠D
1）延长AC到点P
2）延长BC交AD于点P
3）连接BD
已知四边形ABCD，线段BO平分∠ABC，线段OD平分∠ADC
∠O=12 (∠A+∠C)
图示
结论（性质）
证明方法
∠A+∠O=∠1+∠2
口诀：腋下两角之和等于上下两角之和
证明:连接AO
∵∠1是∆ABO的外角 ∴∠1=∠3+∠5 ①
∵∠2是∆ACO的外角 ∴∠2=∠4+∠6 ②
①+②得∠1+∠2=∠3+∠5+∠4+∠6，即
∠1+∠2=∠BAC+∠BOC
∠A+∠O=∠2-∠1
证明：连接AO
∵∠1是∆ABO的外角 ∴∠1=∠BAO+∠AOB ①
∵∠2是∆AOD的外角 ∴∠2=∠3+ BAO +∠AOB+∠BOD ②
②-①得∠2-∠1=∠3+∠BFD 即∠BAD+∠BOD=∠2-∠1
已知
图示
结论（性质）
将三角形纸片ABC沿EF边折叠，当点C落在线段AC上时
∠2=2∠C
将三角形纸片ABC沿EF边折叠，当点C落在四边形ABFE内部时
2∠C=∠1+∠2或 ∠C=12（∠1+∠2）
将三角形纸片ABC沿EF边折叠，当点C落在四边形ABFE外部时
2∠C=∠2-∠1或 ∠C=12（∠2-∠1）
已知
图示
结论（性质）
证明过程
已知BD、DC分别平分∠ABC、∠ACB
∠D=90°+12∠A
证明：∵BD、DC分别平分∠ABC、∠ACB
∴∠DBC=12∠ABC，∠DCB=12∠ACB
∵在∆ABC中，∠A+∠ABC+∠ACB =180°∴∠A=180°-2∠DBC -2∠DCB ①
∵在∆BDC中，∠D+∠DBC+∠DCB=180°∴∠D=180°-∠DBC -∠DCB ②
①-2×②得∠A -2∠D=180°-2∠DBC -2∠DCB-360°+2∠DBC+2∠DCB即∠D=90°+12∠A
已知BD、DC分别平分∠EBC、∠FCB
∠D=90°- 12∠A
证明：∵BD、DC分别平分∠EBC、∠FCB
∴∠1=∠2 = 12∠EBC，∠3=∠4 = 12∠FCB
∵在∆ABC中，∠A+∠ABC+∠ACB =180°∴∠A =180°-(180°-∠1-∠2) –(180°-∠3-∠4)
化简得∠A=∠1+∠2+∠3+∠4-180°=2∠2 +2∠3-180° ①
∵在∆BDC中，∠D+∠2+∠3=180°∴∠D=180°-∠2 -∠3 ②
①+2×②得∠A +2∠D=180°即∠D=90°- 12∠A
已知BE、EC分别平分∠ABC、∠ACD
∠E=12∠A
证明：∵BE、EC分别平分∠ABC、∠ACD
∴∠1=∠2 = 12∠ABC，∠3=∠4 = 12∠ACD
∵∠ACD是∆ABC的外角 ∴∠ACD=∠A+∠ABC即∠A=2∠3-2∠1 ①
∵∠4是∆EBC的外角 ∴∠4=∠E+∠2即∠E=∠4-∠2 ②
①-2×②得∠A-2∠E=0即∠E=12∠A
已知
图示
结论（性质）
∠B=∠D=∠ACE=90°
∠BAC=∠DCE，∠ACB=∠CED