2024版高考数学微专题专练56算法初步理（附解析）

这是一份2024版高考数学微专题专练56算法初步理（附解析），共9页。


[基础强化]
一、选择题
1．用辗转相除法求得168与486的最大公约数是( )
A．3 B．4 C．6 D．16
2．阅读如图所示的程序框图，若输入的a，b，c分别是21，32，75，则输出的a，b，c分别是( )
A．75，21，32
B．21，32，75
C．32，21，75
D．75，32，21
3.
执行如图所示的程序框图，若输出的结果为3，则可输入的实数x值的个数为( )
A．1
B．2
C．3
D．4
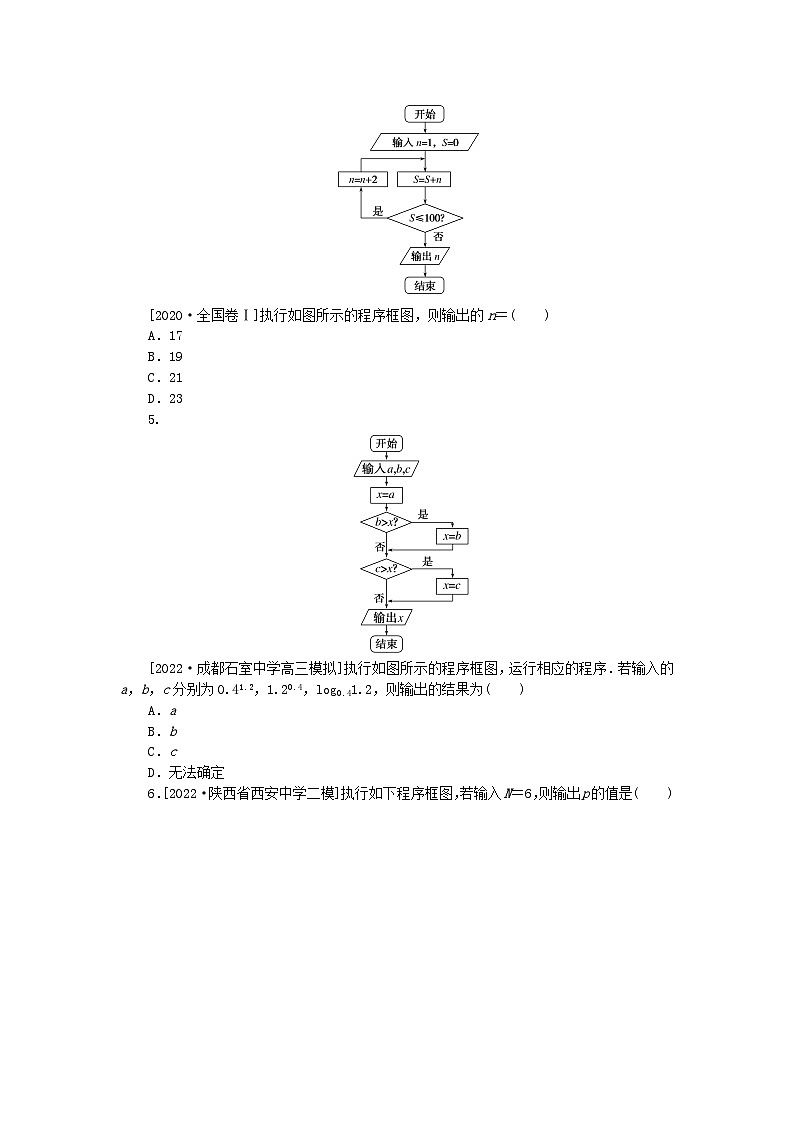
4.
[2020·全国卷Ⅰ]执行如图所示的程序框图，则输出的n＝( )
A．17
B．19
C．21
D．23
5.
[2022·成都石室中学高三模拟]执行如图所示的程序框图，运行相应的程序．若输入的a，b，c分别为0.41.2，1.20.4，lg0.41.2，则输出的结果为( )
A．a
B．b
C．c
D．无法确定
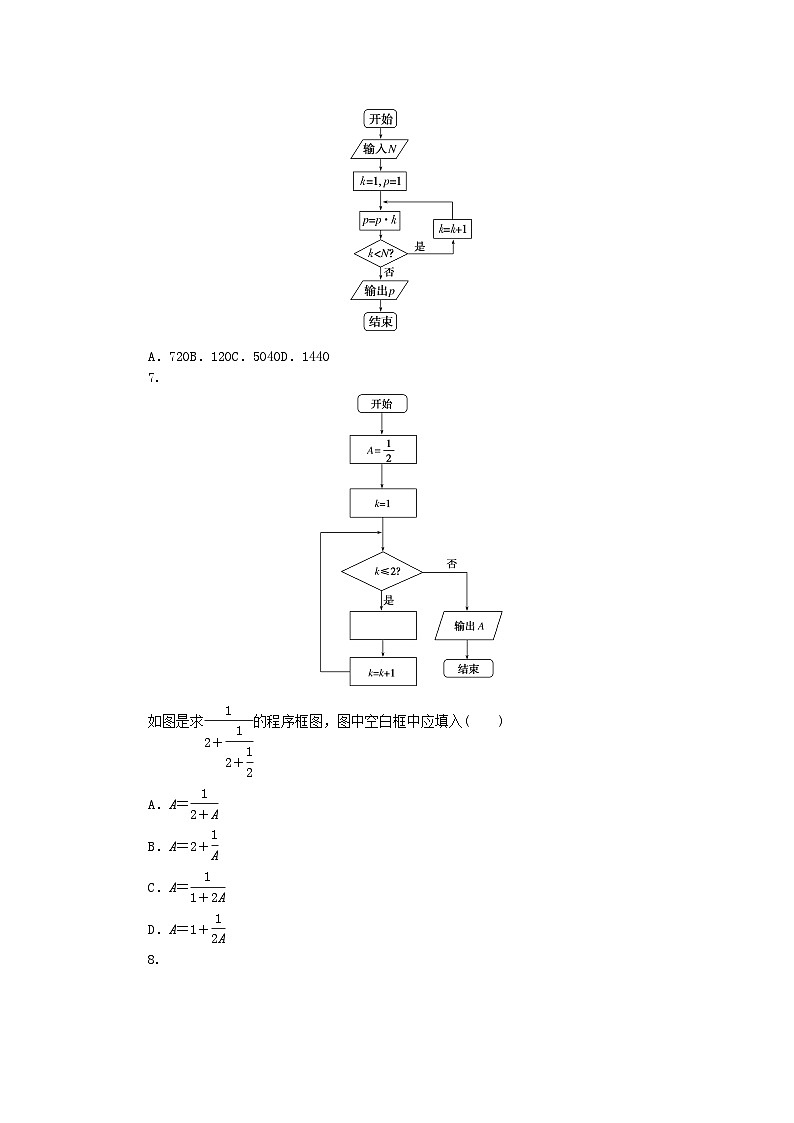
6．[2022·陕西省西安中学二模]执行如下程序框图，若输入N＝6，则输出p的值是( )
A．720B．120C．5040D．1440
7.
如图是求eq \f(1,2＋\f(1,2＋\f(1,2)))的程序框图，图中空白框中应填入( )
A．A＝eq \f(1,2＋A)
B．A＝2＋eq \f(1,A)
C．A＝eq \f(1,1＋2A)
D．A＝1＋eq \f(1,2A)
8.
[2022·安徽省江南十校一模]《九章算术》是中国古代的数学专著，是《算经十书》中最重要的一本，成于公元1世纪左右，该书内容十分丰富，系统总结了战国、秦、汉时期的数学成就，其中第七章“盈不足”中有一道两鼠穿墙问题：今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，问何日相逢？”题意是：“有两只老鼠从厚五尺墙的两边打洞穿墙，大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半．问几日两鼠相逢？”有人设计了如图所示的程序框图解决此问题，则此题的结果为( )
A．2B．3C．4D．5
9.
执行右边的程序框图，如果输入的ε为0.01，则输出s的值等于( )
A．2－eq \f(1,24)
B．2－eq \f(1,25)
C．2－eq \f(1,26)
D．2－eq \f(1,27)
二、填空题
10．如图是一个算法流程图．若输入x的值为eq \f(1,16)，则输出y的值是________．
11．按照如图程序运行，则输出k的值是________．
x＝3
k＝0
D
x＝2*x＋1
k＝k＋1
LOOP UNTIL x>16
PRINT k
END
12．执行如图所示的程序框图，若输入的a，b的值分别是0和9，则输出的i的值为________.
[能力提升]
13．如图程序框图表示的算法的功能是( )
A.计算小于100的奇数的连乘积
B．计算从1开始的连续奇数的连乘积
C．从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数
D.计算1×3×5×…×n≥100时的最小的n值
14.
[2020·全国卷Ⅱ]执行如图的程序框图，若输入的k＝0，a＝0，则输出的k为( )
A．2
B．3
C．4
D．5
15．某流程图如图所示，现输入如下四个函数，则可以输出的函数是( )
A.f(x)＝eq \f(|x|,x)
B．f(x)＝ln (eq \r(x2＋1)－x)
C．f(x)＝eq \f(ex＋e－x,ex－e－x)
D．f(x)＝eq \f(\r(1－x2),|x＋3||4－x|)
16.
[2022·东北三省高三模拟]在爱尔兰小说《格列佛游记》里，有格列佛在小人国一顿吃了1728份小人饭的叙述，作者为什么要使用这么复杂的数字呢？许多研究者认为，之所以选用这个数字，跟英国人计数经常使用的十二进制有关系．中国文化中，十二进制也有着广泛应用，如12地支，12个时辰，12生肖…….十二进制数通常使用数字0～9以及字母A，B表示，其中A即数字10，B即数字11.对于下面的程序框图，若输入a＝1728，k＝12，则输出的数为________．
专练56 算法初步
1．C ∵486＝168×2＋150，168＝150＋18，150＝18×8＋6，18＝3×6，∴168与486的最大公约数为6.
2．A 由程序框图可知x＝21，a＝75，c＝32，b＝21.
3．C 该程序框图表示输入x，输出y＝eq \b\lc\{(\a\vs4\al\c1(lg2x，x>2，,x2－1，x≤2))的函数值，由y＝3，得eq \b\lc\{(\a\vs4\al\c1(lg2x＝3，,x>2，))或eq \b\lc\{(\a\vs4\al\c1(x2－1＝3，,x≤2，))得x＝8或x＝±2，
故可输入的实数x的值的个数为3.
4．C S＝0，n＝1；
S＝1，S≤100，n＝3；
S＝4，S≤100，n＝5；
S＝9，S≤100，n＝7；
……
S＝81，S≤100，n＝19；
S＝100，S≤100，n＝21；
S＝121，S>100，结束循环，
∴输出n的值为21.
5．B 程序框图表示取a，b，c中的最大值，因为0<0.41.2<0.40＝1，即01.20＝1，c＝lg0.41.2a>c，所以a，b，c中的最大值为b.
6．A N＝6，k＝1，p＝1，
①p＝1×1＝1，1<6；
②k＝2，p＝1×2＝2，2<6；
③k＝3，p＝2×3＝6，3<6；
④k＝4，p＝6×4＝24，4<6；
⑤k＝5，p＝24×5＝120，5<6；
⑥k＝6，p＝120×6＝720，6＝6；
输出p＝720.
7．A 当k＝1时，k≤2成立，A＝eq \f(1,2＋A)＝eq \f(1,2＋\f(1,2))；
当k＝2时，k≤2成立，A＝eq \f(1,2＋A)＝eq \f(1,2＋\f(1,2＋\f(1,2)))；
当k＝3时，k≤2不成立，输出A.
8．B 第一次执行得S＝2，S<5，进入循环体得a＝2，b＝eq \f(1,2)，i＝2；
第二次执行得S＝4.5，S<5，进入循环体得a＝4，b＝eq \f(1,4)，i＝3，
第三次执行得S＝8.75，S≥5，满足条件，输出i＝3.
9．C 该程序框图的功能是求和，即s＝1＋eq \f(1,2)＋eq \f(1,22)＋…＋eq \f(1,2n－1)，由于x＝eq \f(1,26)>0.01, x＝eq \f(1,27)<0.01，故当x＝eq \f(1,27)时，结束循环，输出s＝1＋eq \f(1,2)＋…＋eq \f(1,26)＝eq \f(1－\f(1,27),1－\f(1,2))＝2×(1－eq \f(1,27))＝2－eq \f(1,26).
10．－2
解析：∵x＝eq \f(1,16)<1，
∴y＝2＋lg2eq \f(1,16)＝2－4＝－2.
11．3
解析：第一次循环，x＝7，k＝1；第二次循环，x＝15，k＝2；第三次循环，x＝31，k＝3，x>16.终止循环，故输出的k的值为3.
12．3
解析：第一次循环，a＝0＋1＝1，b＝9－1＝8，i＝2；
第二次循环，a＝1＋2＝3，b＝8－2＝6，i＝3；
第三次循环，a＝3＋3＝6，b＝6－3＝3，此时a>b，跳出循环．故输出的i的值为3.
13．D 由题意，此程序框图表示S＝S*i的循环结构，当不满足S≥100时，i＝i＋2，直至满足S≥100，即计算1×3×5×…×n≥100的最小的n的值．
14．C 输入k＝0，a＝0，第一次循环，a＝1，k＝1，a<10，第二次循环，a＝3，k＝2，a<10，第三次循环，a＝7，k＝3，a<10，第四次循环，a＝15，k＝4，a>10，结束循环，输出k＝4.
15．B 从程序框图可以看出，输入的函数是奇函数且有零点，则即可输出该函数．因此答案等价于判断哪个函数是奇函数且有零点．假设输入答案A中的函数，显然A中函数为奇函数，但没有零点，所以不能输出函数；答案B中的函数是奇函数且存在零点0，所以输出函数为f(x)＝ln (eq \r(x2＋1)－x).同理答案C、D不符合题意．
16．1000
解析：输入a＝1728，k＝12，q＝1728÷12＝144…0；
a＝144，k＝12，q＝144÷12＝12…0；
a＝12，k＝12，q＝12÷12＝1…0；
a＝1，k＝12，q＝1÷12＝0…1；
所以输出的数为1000.