北师大版 (2019)选择性必修 第一册3.2 离散型随机变量的方差优秀ppt课件

这是一份北师大版 (2019)选择性必修 第一册3.2 离散型随机变量的方差优秀ppt课件，共41页。PPT课件主要包含了方差定义，可能取值的方差为，是一个常数等内容，欢迎下载使用。

1、离散型随机变量 X 的均值（数学期望）
若随机变量X服从两点分布，则
反映了离散型随机变量取值的平均水平.
设在一组数据x1，x2 ，…， xn中，各数据与它们的平均数的差的平方的平均值是：
叫做这组数据的方差.
方差说明了这组数据的波动情况.
问题1 有两批灯泡，其平均寿命都是1000 h，仅由这一指标还不能判断这两批灯泡质量的好坏.事实上，虽然两批灯泡的平均寿命相当，但有可能其中一批灯泡大部分的寿命集中在950 h〜1 050 h；而另一批灯泡有可能一部分寿命很长，能达到1500 h，另一部分寿命很短，只能达到500 h左右.因此，为了判断灯泡质量的好坏，还需要进一步考察灯泡寿命X与其均值EX的偏离程度.若偏离程度小，则灯泡的寿命比较稳定；若偏离程度大，则灯泡寿命的稳定性比较差.
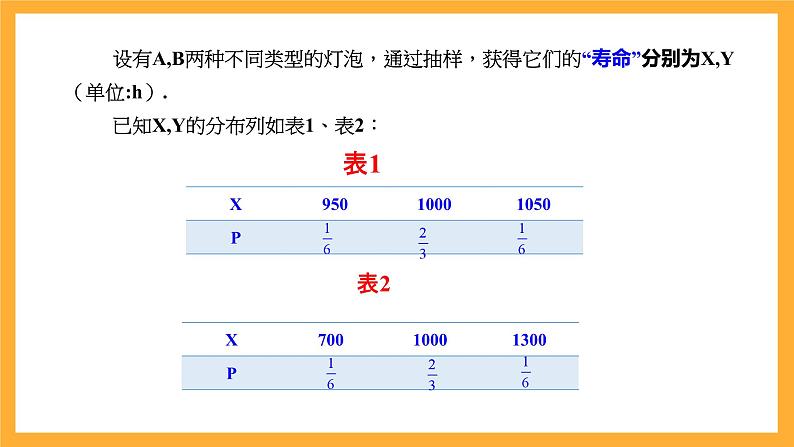
设有A,B两种不同类型的灯泡，通过抽样，获得它们的“寿命”分别为X,Y（单位:h）. 已知X,Y的分布列如表1、表2：
根据X,Y的分布列计算可得EX=EY=1000 h,也就是这两种灯泡的平均寿命都是1000 h.进一步观察，我们可以发现，A类型的灯泡寿命介于950 h〜1050 h，B类型的灯泡寿命介于700 h〜1300 h，直观上看，A类型的灯泡寿命X与其均值的偏离程度要小一些.
思考：怎样定量刻画随机变量的离散程度？
(1).样本的离散程度是用哪个量刻画的？
(2).能否用一个与样本方差类似的量来刻画随机变量的稳定性呢？
对于离散型随机变量X的概率分布如下表：
(xi－ E(X))2 描述了xi (i=1，2，…，n)相对于均值E(X)的偏离程度，故(x1－E(X))2 p1＋ (x2－E(X))2 p2＋...＋ (xn－E(X))2pn
离散型随机变量的方差定义
(其中pi≥0，i＝1，2，…，n；p1＋p2＋…＋pn＝1)
称为离散型随机变量X的方差，记为D(X).
随机变量的方差与标准差都反映了随机变量取值的稳定与波动，集中与分散的程度.
上式为这些偏离程度的加权平均，刻画了随机变量X与其均值EX的平均偏离程度.我们称DX为随机变量X的方差，其算术平方根 为随机变量X 的标准差，记作 .随机变量的方差DX和标准差 都反映了随机变量的取值偏离于均值的平均程度.方差(标准差) 越小,则随机变量偏离于均值的平均程度越小；反之，方差(标准差)越大，则随机变量的取值越分散.
在问题1中,A类型灯泡寿命X的方差为
显然，A类型灯泡的方差要小，质量要好.
如何评价这两名同学的射击水平？
问题2：从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录，甲、乙两名同学击中目标靶的环数X和Y的分布列如下表1和表2所示：
表1 表2
即乙同学的射击成绩相对更稳定.
D(X)1.16,D(Y)0.92.
E(X)8,E(Y)8.
因为 D(Y) D(X) (等价地 D(Y)  D(X) ) ，所以随机变量Y的取值相对更集中，
方差用处大--万紫千红总是春1.制造业中，质量控制指标
2.农业中，作物长势比较及利润决策
4.数学建模中，用于模型评估
统计分析3.金融领域中，可用于风险评估
批判质疑出真知--曲径通幽是智者，大起大落亦精彩
质疑：均值相等，方差是否越小越好？
D(X) (xi  E(X))2 pi
公式化简--行到水穷处，坐看云起时
问题3：方差的计算公式可以简化吗？ni1
线性性质--行到水穷处，坐看云起时问题4：离散型随机变量X加上一个常数，方差会有怎样变化？离散型随机变量X乘以一个常数，方差又有怎样的变化？它们和期望的性质有什么不同？
D(X b)  D(X)D(aX)  a2D(X)
D(aX+b)=a2D(X)
2．有甲、乙两种水稻，测得每种水稻各10株的分蘖数据，计算出样本方差分别为DX甲＝11，DX乙＝3.4.由此可以估计(　　)A．甲种水稻比乙种水稻分蘖整齐B．乙种水稻比甲种水稻分蘖整齐C．甲、乙两种水稻分蘖整齐程度相同D．甲、乙两种水稻分蘖整齐程度不能比较
解析：因为D(X甲)>D(X乙)，所以乙种水稻比甲种水稻分蘖整齐．故选B.
3．已知X的分布列为则DX等于(　　)A．0.7　　　　B．0.61　　　　C．－0.3　　　　D．0
解析：EX＝－1×0.5＋0×0.3＋1×0.2＝－0.3，DX＝0.5×(－1＋0.3)2＋0.3×(0＋0.3)2＋0.2×(1＋0.3)2＝0.61.
随机变量X的方差与X可能取值的方差何时相等
① 随机变量的方差是常数, 样本的方差是随机变量;② 对于简单随机样本,随着样本容量的增加,样本平均值越来越接近于总体方差，因此常用样本方差来估计总体方差
随机变量的方差与样本的方差有何区别和联系？
随着不同样本值的变化而变化
随着不同样本值的变化而变化，反映数据偏离平均数的平均程度，方差越小，偏离程度越小.
是一个常数，反映随变量取值偏离均值的平均程度，方差越小，偏离程度越小.
例1．随机抛掷一枚质地均匀的骰子,求向上一面的点数X的均值、方差和标准差.
解：抛掷骰子所得点数X 的分布列为
例2 甲、乙两名工人加工同一种零件，两人每天加工的零件数相等，设ξ，η分别表示 甲、乙两人所加工出的次品件数，且E和卩的分布列分别如表1、表2：
试比较这两名工人谁的技术水平更高.
即Eξ=Eη，说明甲、乙两名工人所加工出的平均次品件数相同，可以认为他们的技术水平相当.
所以Dξ>Dη ，说明工人乙的技术比较稳定.
1. 已知随机变量X的分布列
2. 若随机变量X 满足P（X＝c）＝1，其中c为常数，求EX 和 DX.
DX＝（c－c）2×1＝0
可以证明, 对于方差有下面三个重要性质：
结论2：若ξ服从两点分布，则 Eξ= np.
1. 若X是一个随机变量，则E(X－EX)的值为(　　)A．无法求　　B．0　　　　C．EX　　　　D．2EX
解析 ∵EX是一个常数，∴E(X－EX)＝EX－EX＝0．
2. 已知随机变量X的分布列是则DX等于(　　)A．0　 　B．0.8　　 C．2　 　D．1
解析 ∵EX＝1×0.4＋2×0.2＋3×0.4＝2，∴DX＝0.4×(1－2)2＋0.2×(2－2)2＋0.4×(3－2)2＝0.8．
3. 随机变量ξ的分布列如下：其中a＋c＝2b，若Eξ＝，则Dξ＝________．
解析 由题意得2b＝a＋c ①，a＋b＋c＝1 ②，c-a＝ ③，以上三式联立解得a= ，b= ，c= ，故Dξ= ．
4．已知离散型随机变量X的概率分布列为则其方差DX＝(　　)A.1 B．0.6 D．2.4
5．在某公司的一次投标工作中，中标可以获利12万元，没有中标损失成本费0.5万元．若中标的概率为0.6，设公司盈利为X万元，则DX＝(　　)A.7 B． D．42.5
7．若某事件在一次试验中发生次数的方差等于0.25，则该事件在一次试验中发生的概率为________．
解析：设事件在一次试验中发生的概率为p，由题意知，事件在一次试验中发生的次数X服从两点分布，即
∴EX＝p.∴DX＝(0－p)2×(1－p)＋(1－p)2×p＝p(1－p)＝0.25解得p＝0.5.
8．甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相等．两个保护区内每个季度发现违反保护条例的事件次数的分布列分别为：
试评定这两个保护区的管理水平．
解析：甲保护区的违规次数X的数学期望和方差分别为：EX＝0×0.3＋1×0.3＋2×0.2＋3×0.2＝1.3；DX＝(0－1.3)2×0.3＋(1－1.3)2×0.3＋(2－1.3)2×0.2＋(3－1.3)2×0.2＝1.21.乙保护区的违规次数Y的数学期望和方差分别为：EY＝0×0.1＋1×0.5＋2×0.4＝1.3；DY＝(0－1.3)2×0.1＋(1－1.3)2×0.5＋(2－1.3)2×0.4＝0.41.因为EX＝EY，DX>DY，所以两个保护区内每季度发生的平均违规次数是相同的，但乙保护区内的违规事件次数更集中和稳定，而甲保护区的违规事件次数相对分散，故乙保护区的管理水平较高．
9.随机抽取某厂的某种产品200件，经质检，其中有一等品126件，二等品50件，三等品20件，次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而生产1件次品亏损2万元，设1件产品的利润（单位：万元）为ξ.(1)求ξ的分布列；（2）求1件产品的平均利润（即ξ的数学期望）；（3）经技术革新后，仍有四个等级的产品，但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？
分析 求ξ的分布列时，要先求ξ取各值时的概率.
解 （1）ξ的所有可能取值有6,2,1,-2……………………1′P(ξ=6)= =0.63,…………………………………..2′P(ξ=2)= =0.25,…………………………………..3′P(ξ=1)= =0.1,…………………………………4′P(ξ=-2)= …………………………………..5′故ξ的分布列为 ……………………………………………………………………7′
(2)E(ξ)=6×0.63+2×0.25+1×0.1+（-2）×0.02=4.34 ………………………………………………………………..9′(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为E(ξ)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29)……………………………………….12′依题意，E(ξ)≥4.73,即4.76-x≥4.73,解得x≤0.03……13′所以三等品率最多为3%′