






高中数学北师大版 (2019)选择性必修 第一册第三章 空间向量与立体几何2 空间向量与向量运算2.1 从平面向量到空间向量完美版课件ppt
展开既有大小又有方向的量。
在平面中,把既有大小又有方向的量称为向量。
表示向量 的有向线段的长度叫做向量 的长度或模.用 表示
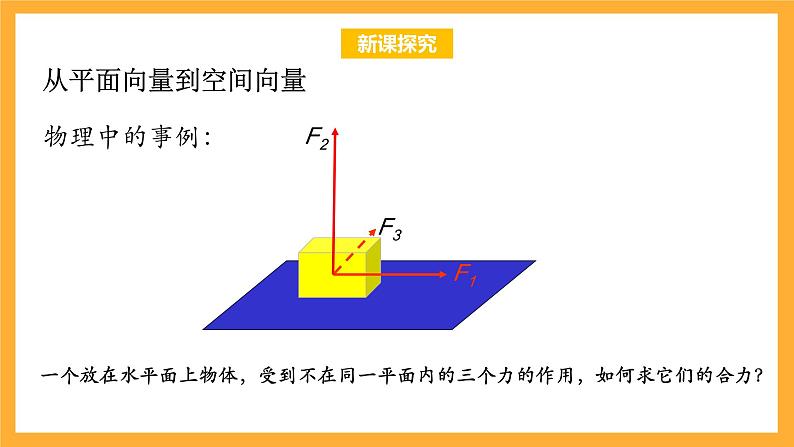
一个放在水平面上物体,受到不在同一平面内的三个力的作用,如何求它们的合力?
某同学从学校大门口出发,向北行走100m,再向东行走200m,最后上电梯15m到达住处.
如何表示该同学从学校门口到住处的位移?
2、两个常见的空间向量:
方向相同且模相等的向量称为相等向量.
方向相反且模相等的向量互为相反向量.
表示向量的两条有向线段所在的直线平行或重合时,称这两个向量互为共线向量(或平行向量)
思考 我们应该如何定义空间中的向量呢?
在空间中,我们把具有大小和方向的量称为空间向量。
思考 通过比较平面向量与空间向量的定义,你有什么发现?
思考 由平面向量到空间向量的定义用到了什么方法?用此方法你能否定义空间向量的其他相关概念?
①若两个空间向量相等,则它们的起点相同,终点相同;
②若空间向量 满足 则 ;
③空间中任意两个模为1的向量必相等;
⑤在空间中任意一个向量都可以进行平移;
⑥两个有公共终点的向量,一定是共线向量.
如图所示,在三棱柱ABC-A1B1C1中,E、F分别是AB,A1B1的中点.
思考 空间中任意两个非零向量是否共面?三个向量呢?
我们把能平移到同一平面内的向量,叫作共面向量.
思考 你能在平行六面体中,找出共线向量和共面向量的实例吗?
1、平面向量的加法、减法
向量加法的平行四边形法则
2、平面向量的加法运算律
3.推广:(1)首尾相接的若干向量之和,
(2)首尾相接的若干向量若构成一个封闭图形,则它们的和为:
等于由起始向量的起点指向末尾向量的终点的向量;
类于平面向量的加法的三角形法则
类于平面向量的加法的平行四边形法则
类于平面向量的减法的三角形法则
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示.因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
加法:三角形法则或平行四边形法则
空间向量的加法、减法运算
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
(2)首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
对空间向量的加法、减法的说明
⒈ 空间向量的运算就是平面向量运算的推广.
⒉ 两个向量相加的平行四边形法则在空间仍然成立.
⒊ 空间向量的加法运算可以推广至若干个向量相加.
平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共起点为起点的对角线所示向量
当 时,
当 时,
与向量 方向相同;
的长度是 的长度的 倍.
一.空间向量的数乘运算
2.空间向量的数乘运算满足分配律及结合律
的充要条件是:存在唯一
的实数 ,使
能否推广到空间向量中呢?
所在直线有那些位置关系?
零向量与任意向量共线.
共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
由此可判断空间中两直线平行或三点共线问题
共线向量定理: 对空间任意两个向量 , , 的充要条件是存在唯一实数λ,使 (也称“一维向量基本定理)
如图,l 为经过已知点A且平行已知非零向量 的直线,
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.由此可判断空间任意三点共线。.
若点P是直线l上任意一点,则
由 知存在唯一的t, 满足
特别的,当t= 时,
1.共面向量:平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任意三个向量
既可能共面,也可能不共面
由平面向量基本定理知,如果 , 是平面内的两个不共线的向量,那么对于这一平面内的任意向量 , 有且只有一对实数 ,使
如果空间向量 与两不共线向量 , 共面,那么可将三个向量平移到同一平面 ,则有
那么什么情况下三个向量共面呢?
反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位置关系?
2.共面向量定理:如果两个向量 , 不共线,
则向量 与向量 , 共面的充要条件是
推论:空间一点P位于平面ABC内的充要条件是存在有序实数对x,y使
式称为空间平面ABC的向量表示式,空间中任意平面由空 间一点及两个不共线的向量唯一确定.
由此可判断空间任意四点共面
练习.若对任一点O和不共线的三点A、B、C,且有
则x+y+z=1是四点P、A、B、C共面的( )
D.既不充分也不必要条件
思考:1、〈a,b〉与〈b,a〉相等吗? 2、〈a,b〉与〈a,-b〉相等吗?
注意:〈a,b〉=〈b,a〉,〈a,-b〉=π-〈a,b〉
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
注: ①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
空间向量数量积运算律
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 两向量的数量积是实数.( )
2.向量a、b之间的夹角为30°,且|a|=3,| b |=4,则a·b =________, a2=________, (a+2b)·(a-b)=_______.
三、投影向量与投影数量
数乘:ka,k为正数,负数,零
高中数学北师大版 (2019)选择性必修 第一册2.2 空间向量的运算优秀ppt课件: 这是一份高中数学北师大版 (2019)选择性必修 第一册<a href="/sx/tb_c4017376_t3/?tag_id=26" target="_blank">2.2 空间向量的运算优秀ppt课件</a>,共27页。PPT课件主要包含了知识回顾,新课探究,横纵竖,应用4判定垂直,巩固提升,距离公式,课堂小结等内容,欢迎下载使用。
高中数学北师大版 (2019)选择性必修 第一册3.1 空间向量基本定理说课课件ppt: 这是一份高中数学北师大版 (2019)选择性必修 第一册3.1 空间向量基本定理说课课件ppt,共60页。PPT课件主要包含了目录索引,本节要点归纳等内容,欢迎下载使用。
北师大版 (2019)选择性必修 第一册2.2 空间向量的运算多媒体教学课件ppt: 这是一份北师大版 (2019)选择性必修 第一册2.2 空间向量的运算多媒体教学课件ppt,共60页。PPT课件主要包含了目录索引,本节要点归纳等内容,欢迎下载使用。













