









北师大版 (2019)选择性必修 第一册2.1 从平面向量到空间向量评课ppt课件
展开1.经历由平面向量推广到空间向量的过程,了解空间向量的概念.2.经历由平面向量的运算及其法则推广到空间向量的过程.3.掌握空间向量的线性运算.
在空间向量概念的形成和进行线性运算的过程中,经历由具体到抽象、由图形语言到符号语言的表达过程,发展学生的直观想象、数学抽象和数学运算素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
一、空间向量的有关概念1.思考 想象一个滑翔伞运动的场景,在滑翔过程中,飞行员受到来自不同方向,大小各异的力,如绳索的拉力、风力、重力等,这些力在同一平面内吗?在数学上,我们把这些力称为什么?提示 这些力不在同一平面内.在数学上,我们把这些力称为空间向量.2.思考 在平面向量中,相等向量、相反向量、共线向量(平行向量)是如何定义的?提示 模相等、方向相同的两个向量叫作相等向量.模相等、方向相反的两个向量叫作相反向量.方向相同或相反的两个向量称为共线向量(平行向量).
3.填空 (1)在空间中,把具有______和______的量叫作空间向量.向量的大小叫作向量的______或____.空间向量用有向线段表示,表示向量a的有向线段的长度也叫作向量a的长度或模,用________表示.有向线段的方向表示向量的方向.
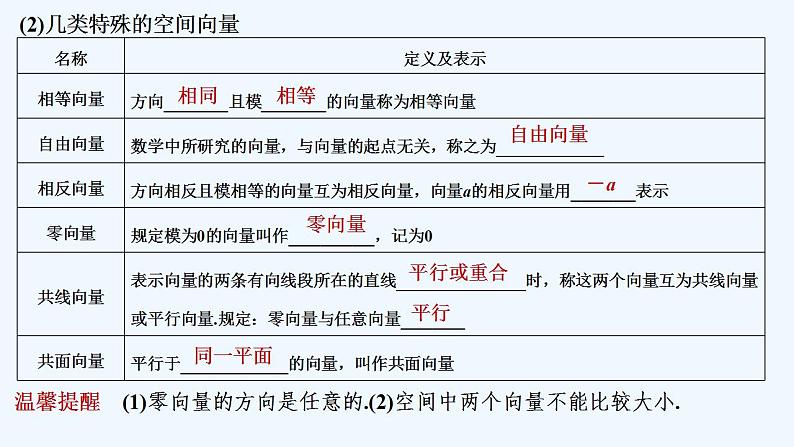
(2)几类特殊的空间向量
温馨提醒 (1)零向量的方向是任意的.(2)空间中两个向量不能比较大小.
4.做一做 (1)判断正误①若向量a与b都是单位向量,则a=b.( )提示 若a与b都是单位向量,则|a|=|b|,但方向可能不同,故未必有a=b.②若a=-b,则|a|=|b|.( )③若两个向量的终点重合,则这两个向量的方向相同.( )提示 两个向量的终点重合,但起点可能不同,则其方向的关系不能确定.
(2)(多选)下列命题中,真命题是( )A.同平面向量一样,任意两个空间向量都不能比较大小B.两个相等的向量,若起点相同,则终点也相同C.只有零向量的模等于0D.共线的单位向量都相等解析 容易判断D是假命题,共线的单位向量是相等向量或相反向量.
二、空间向量的加减运算1.思考 空间中的任意两个向量是否共面?为什么?提示 共面,任意两个向量都可以平移到同一平面内.
提示 借助平行四边形法则或三角形法则运算.
温馨提醒 (1)求向量和时,可以首尾相接,也可共起点;求向量差时,可以共起点.(2)注意向量0与数字0的区别.(3)向量和与差仍然是向量.
三、空间向量的数乘运算1.思考 在平面向量中的数乘运算的方向和大小是如何定义的?提示 实数λ与向量a的积是一个向量,记作λa,其长度和方向规定如下:(1)|λa|=|λ||a|.(2)当λ>0时,λa与a同向;当λ<0时,λa与a反向;当λ=0时,λa=0.
温馨提醒 (1)当λ=0或a=0时,λa=0.(2)λ的正负影响着向量λa的方向,λ的绝对值的大小影响着λa的长度.(3)向量λa与向量a一定是共线向量.
解析 根据空间向量的数乘运算法则可知,
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
解析 ①错误,向量a,b平行,则a,b所在的直线平行或重合;②错误,|a|=|b|只能说明a,b的长度相等而方向不确定;③错误,向量不能比较大小;④正确;
空间向量的概念与平面向量的概念类似,平面向量中的向量的模、相等向量、平行向量、相反向量、单位向量等都可以拓展为空间向量的对应概念.
空间向量加法、减法运算的两个技巧(1)巧用相反向量:向量的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.(2)巧用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得运算结果.
解 ∵P是C1D1的中点,
解 ∵N是BC的中点,
解 ∵M是AA1的中点,
利用数乘运算进行向量表示的技巧(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
1.牢记三个知识点:(1)向量的有关概念.(2)向量的线性运算.(3)向量的线性运算的运算律.2.掌握两种方法:类比转化、数形结合.3.辨清一个易错点:向量线性运算的结果仍然是向量.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.下列命题中不正确的是( )A.如果a,b是两个单位向量,则|a|=|b|B.两个空间向量相等,则它们的起点相同,终点也相同C.若a,b,c为任意向量,则(a+b)+c=a+(b+c)D.空间任意两个非零向量都可以平移到同一个平面内解析 由单位向量的定义知|a|=|b|=1,故A正确;因相等向量不一定有相同的起点和终点,所以B错误;由向量加法运算律知C正确;在空间确定一点后,可将两向量的起点移至该点,这两个非零向量就同在一个平面内,故D正确.
解析 易知四边形EFGH为平行四边形,
解析 如图所示:M,N分别为AD,B1C1的中点,O1,O2分别为上下底面的中心,
如图,连接DA1,则1即为所求.
解 如图,取AA′的中点E,在D′C′上取一点F,使|D′F|=2|FC′|,连接EF,
高中数学人教A版 (2019)选择性必修 第一册1.2 空间向量基本定理图片免费ppt课件: 这是一份高中数学人教A版 (2019)选择性必修 第一册1.2 空间向量基本定理图片免费ppt课件,文件包含第一课时空间向量及其线性运算pptx、第一课时空间向量及其线性运算DOCX等2份课件配套教学资源,其中PPT共51页, 欢迎下载使用。
【最新版】高中数学(新北师大版)习题+同步课件限时小练29 空间向量运算的坐标表示及应用: 这是一份【最新版】高中数学(新北师大版)习题+同步课件限时小练29 空间向量运算的坐标表示及应用,文件包含限时小练29空间向量运算的坐标表示及应用pptx、限时小练29空间向量运算的坐标表示及应用docx等2份课件配套教学资源,其中PPT共5页, 欢迎下载使用。
【最新版】高中数学(新北师大版)习题+同步课件限时小练26 空间向量的加减与数乘运算: 这是一份【最新版】高中数学(新北师大版)习题+同步课件限时小练26 空间向量的加减与数乘运算,文件包含限时小练26空间向量的加减与数乘运算pptx、限时小练26空间向量的加减与数乘运算docx等2份课件配套教学资源,其中PPT共5页, 欢迎下载使用。













