


所属成套资源:2023-2024学年苏教版选择性必修第一册课件(40份)
苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用教课内容ppt课件
展开
这是一份苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用教课内容ppt课件,共9页。PPT课件主要包含了情境问题,学生活动,数学建构,数学应用等内容,欢迎下载使用。
复习1:函数极值的定义是什么?函数的极大值、极小值统称为函数的极值.
探究1:求可导函数 的极值的步骤.①确定函数的定义区间,求导数 ;②求方程 的根.
③用函数的导数为 0 的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查 在方程根左右的值的符号,如果左正右负,那么 在这个根处取得极大值;如果左负右正,那么 在这个根处取得极小值;如果左右不改变符号,那么 在这个根处无极值.
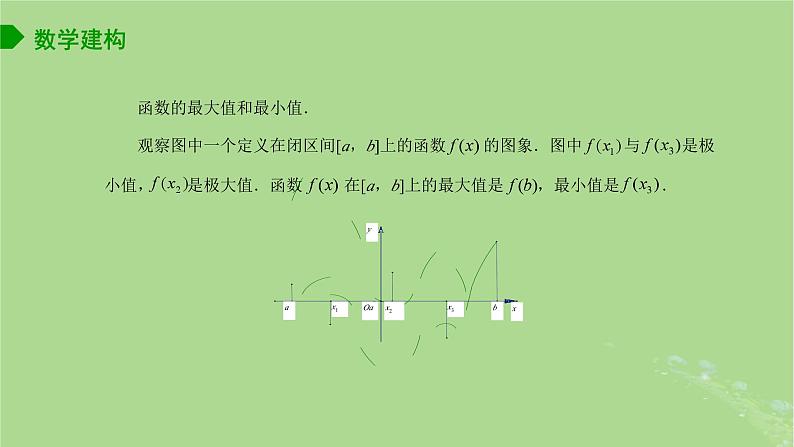
函数的最大值和最小值.观察图中一个定义在闭区间[a,b]上的函数 的图象.图中 与 是极小值, 是极大值.函数 在[a,b]上的最大值是 ,最小值是 .
说明:(1)在开区间(a,b)内连续的函数 不一定有最大值与最小值.如函数 在(0,+∞) 内连续,但没有最大值与最小值;(2)函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的;(3)函数 在闭区间[a,b]上连续,是 在闭区间[a,b]上有最大值与最小值的充分条件而非必要条件;(4)函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个.
利用导数求函数的最值步骤.由上面函数的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.设函数 在[a,b]上连续,在[a,b]内可导,则求 在区间[a,b]上的最大值与最小值可以分为两步:(1)求 在区间 上的极值;(2)将(1)中求得的极值与 、 比较,得到 在区间[a,b]上的最大值与最小值.
例1 求 在区间[-1,4]上的最大值与最小值.解 . 令 ,解得 .列表如下表所示.从上表可知,函数 在区间[-1,4]上的最大值是8,最小值是-1.
例2 求 在区间[0,2π]上的最大值与最小值.解 . 令 ,解得 , .列表如下表所示.从上表可知,函数 在区间[0,2π]上的最大值是 π,最小值是 0.
相关课件
这是一份数学选择性必修第一册5.3 导数在研究函数中的应用说课课件ppt,共10页。PPT课件主要包含了情境问题,学生活动,数学应用等内容,欢迎下载使用。
这是一份高中数学苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用课文内容ppt课件,共35页。
这是一份苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用作业课件ppt,共23页。PPT课件主要包含了A层基础达标练,B层能力提升练,ACD,C层拓展探究练等内容,欢迎下载使用。









