2023年秋人教版九年级数学上册期末试题（含答案）

这是一份2023年秋人教版九年级数学上册期末试题（含答案），共10页。试卷主要包含了 单选题， 填空题， 解答题等内容，欢迎下载使用。

一、 单选题 （本题共计12小题，总分48分）
1.（4分）下列图形是中心对称图形的是( )
A.B.C.D.
2.（4分）将一元二次方程x2−2x−2＝0配方后所得的方程是( )
A.(x−2)2=2B.(x−1)2=2C.(x−1)2=3D.(x−2)2=3
3.（4分）将抛物线y＝(x+1)2向下平移2个单位，再向右平移1个单位，所得到的抛物线是( )
A.y=(x+2)2+2B.y=(x+2)2—2C.y=x2+2D.y=x2—2
4.（4分）下列事件属于必然事件的是( )
A.经过交通信号的路口,遇到红灯
B.任意买一张电影票,座位号是双号
C.向空中抛一枚硬币,不向地面掉落
D.三角形中,任意两边之和大于第三边
5.（4分）下列说法正确的是( )
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.垂直于弦的直线平分弦
6.（4分）PA,PB是⊙O的切线，A，B是切点，点C是⊙O上不同于A、B的一个点，若∠P＝40°，则∠ACB的度数是( )
A.70°B.110°C.70°或110°D.80°或100°
7.（4分）在Rt△ABC中，∠C＝90°，AC＝12，BC＝5，将△ABC绕边AC所在直线旋转一周得到圆锥，则该圆锥的侧面积是( )
A.25πB.65πC.90πD.130π
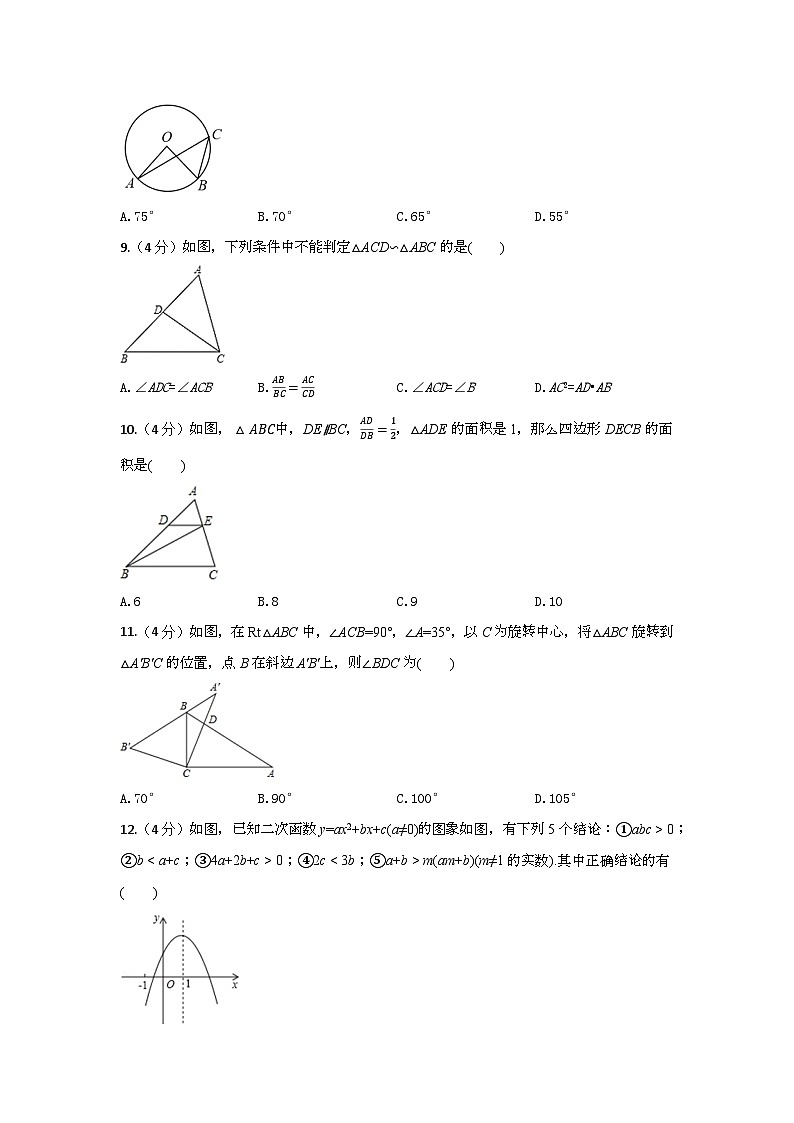
8.（4分）如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是( )
A.75°B.70°C.65°D.55°
9.（4分）如图，下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACBB.ABBC=ACCDC.∠ACD=∠BD.AC2=AD•AB
10.（4分）如图，△ABC中，DE∥BC，ADDB=12，△ADE的面积是1，那么四边形DECB的面积是( )
A.6B.8C.9D.10
11.（4分）如图，在Rt△ABC中，∠ACB=90°，∠A=35°，以C为旋转中心，将△ABC旋转到△A′B′C的位置，点B在斜边A′B′上，则∠BDC为( )
A.70°B.90°C.100°D.105°
12.（4分）如图，已知二次函数y=ax2+bx+c(a≠0)的图象如图，有下列5个结论：①abc > 0；②b < a+c；③4a+2b+c > 0；④2c < 3b；⑤a+b > m(am+b)(m≠1的实数).其中正确结论的有( )
A.①②③B.①③④C.③④⑤D.②③⑤
二、 填空题 （本题共计6小题，总分24分）
13.（4分）已知坐标系中点A(−2,a)和点B(b,3)关于原点中心对称，则a+b=__________.
14.（4分）在不透明的盒子中装有5个黑色棋子和若干个白色做子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是14，则白色棋子的个数是_____.
15.（4分）一个正多边形的每个内角等于108°，则它的边数是_____.
16.（4分）如图，AB、AC是⊙O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N.如果MN=2.5，那么BC=_____.
17.（4分）如图，△ABC的顶点A在反比例函数y=kx(x>0)的图象上，顶点C在x轴上，AB∥x轴，若点B的坐标为(1，3)，S△ABC=2，则k=_____.
18.（4分）如图，点C在以AB为直径的半圆上，AB=10，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F.下列结论：①CE=CF；②线段EF的最小值为53；③当AD=3时，EF与半圆相切；④若点F恰好落在弧BC上，则AD=5；⑤当点D从点A运动到B点时，线段EF扫过的面积是203.其中正确结论的序号是_____.
三、 解答题 （本题共计7小题，总分78分）
19.（10分）用适当的方法解下列方程.
(1)(x+2)2=2x+4
(2)3x2−1=4x
20.（10分）如图，在边长为1个单位长度的小正方形网格中：
(1)画出△ABC向上平移6个单位长度，再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2.
(3)求△CC1C2的面积.
21.（10分）某学校为了增强学生体质，决定开设以下体育课外活动项目：A篮球、B乒乓球、C跳绳、D踢毽子，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
(1)这次被调查的学生共有人；
(2)请你将条形统计图补充完成；
(3)在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
22.（10分）洋洋百货于去年年初以每件25元的进价购进一批商品.当商品售价为40元时，一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上，三月底的销售量达到400件.设二、三这两个月月平均增长率不变.
(1)求二、三这两个月的月平均增长率；
(2)从四月份起，商场决定采用降价促销的方式回馈顾客，经调查发现，该商品每降价1元，销售量增加5件，当商品降价多少元时，商场获利4250元？
23.（12分）如图，已知反比例函数y＝kx的图象与一次函数y＝x+b的图象交于点A(1,4),点B(−4,n).
(1)求n和b的值；
(2)求△OAB的面积；
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围
24.（12分）如图，△ABC为⨀O的内接三角形，AD⊥BC，垂足为D，直径AE平分∠BAD，交BC于点F，连结BE.
(1)求证：∠AEB=∠AFD；
(2)若AB=10,BF=5，求DF的长；
25.（14分）如图，已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(−3,0)，与y轴交于点C，且OC=OB.
(1)求此抛物线的解析式；
(2)若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值,并求出此时点E的坐标；
(3)点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标.
答案
一、 单选题 （本题共计12小题，总分48分）
1.（4分）【答案】D
2.（4分）【答案】C
3.（4分）【答案】D
4.（4分）【答案】D
5.（4分）【答案】B
6.（4分）【答案】C
7.（4分）【答案】B
8.（4分）【答案】B
9.（4分）【答案】B
10.（4分）【答案】B
11.（4分）【答案】D
12.（4分）【答案】C
二、 填空题 （本题共计6小题，总分24分）
13.（4分）【答案】−1;
14.（4分）【答案】15;
15.（4分）【答案】五；
16.（4分）【答案】5；
17.（4分）【答案】7；
18.（4分）【答案】①②④
三、 解答题 （本题共计7小题，总分78分）
19.（10分）(1)x1=0,x2=−1；
(2)x1=2+73,x2=2−73
20.（10分）(1)略；
(2)略；
(3)9
21.（10分）(1)200；
(2)60；
(3)16,
22.（10分）(1)25%；
(2)5
23.（12分）(1)n=−1,b=3；
(2)7.5；
(3)x>1或−424.（12分）(1)证明：∵AE为⨀O的直径，
∴∠ABE＝90°，
∴∠BAE+∠AEB＝90°，
∵AD⊥BC，
∴∠ADF＝90°，，
∴∠AFD+∠FAD＝90°，
∵AE平分∠BAD，
∴∠BAE＝∠FAD，
∴∠AEB＝∠AFD；
(2)解：如图1，过点F作FM⊥AB于点M.则∠AMF＝90°，
∵∠AFD＝∠BFE，∠AFD＝∠AEB，
∴∠BFE＝∠AEB，
∴BF＝BE＝5，
∵∠ABE＝∠AMF＝90°，∠BAE＝∠MAF，
∴△AMF∽△ABE，
∴AMAB=MFBE，
即AMMF=ABBE=105=2，
设MF＝x，则AM＝2x，
∴BM＝10−2x，
∵BM2+MF2＝BF2，
∴(10−2x)2+x2＝52，
解得x＝3，
即MF＝3，
∵AE平分∠BAD，AD⊥BC，
∴DF＝MF＝3；
25.（14分）(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1，0)和点B(﹣3，0)，
∴OB=3，
∵OC=OB，
∴OC=3，
∴c=3，
∴{a+b+3=09a−3b+3=0，解得：{a=−1b=−2，
∴所求抛物线解析式为：y=−x2−2x+3；
(2)如图2，过点E作EF⊥x轴于点F，设E(a，−a2−2a+3)(﹣3 < a < 0)，
∴EF=−a2−2a+3，BF=a+3，OF=﹣a，
∴S四边形BOCE=SΔBEF+S梯形FOCE=12BF•EF+12(OC+EF)•OF=12(a+3)(−a2−2a+3)+12(−a2−2a+6)(−a)=−32a2−92a+92=−32(a+32)2+638，
∴当a=−32时，S四边形BOCE最大，且最大值为638.
此时，点E坐标为(−32，154)；
(3)∵抛物线y=−x2−2x+3的对称轴为x=﹣1，点P在抛物线的对称轴上，
∴设P(﹣1，m)，
∵线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，如图，
∴PA=PA′，∠APA′=90°，
如图3，过A′作A′N⊥对称轴于N，设对称轴与x轴交于点M，
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°，
∴∠NA′P=∠MPA，
在△A′NP与△APM中，∵∠A′NP=∠AMP=90°，∠NA′P=∠MPA，PA′=AP，
∴△A′NP≌△PMA，
∴A′N=PM=|m|，PN=AM=2，
∴A′(m﹣1，m+2)，
代入y=−x2−2x+3得：m+2=−(m−1)2−2(m−1)+3，
解得：m=1，m=﹣2，
∴P(﹣1，1)，(﹣1，﹣2).