2023年秋人教版八年级数学上册期末试题3（含答案）

这是一份2023年秋人教版八年级数学上册期末试题3（含答案），共10页。试卷主要包含了 单选题， 填空题， 解答题等内容，欢迎下载使用。

一、 单选题 （本题共计12小题，总分48分）
1.（4分）下列图形中，既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
2.（4分）衡量样本和总体的波动大小的特征数是( )
A.平均数B.众数C.方差D.中位数
3.（4分）用配方法解方程x2−2x−3=0，下列配方正确的是( )
A.(x−1)2=1B.(x+1)2=1C.(x−1)2=4D.(x+1)2=4
4.（4分）如图，若矩形ABCD的对角线AC，BD相交于点O，OA＝3，则OB的长为( )
A.4B.3C.2D.1
5.（4分）已知点M(a,−2)与点N(3,b)关于原点对称，则a+b的值是( )
A.−1B.1C.−6D.9
6.（4分）二次函数y＝2x2﹣3的图象是一条抛物线，下列关于该抛物线的说法，正确的是( )
A.抛物线开口向下B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1D.抛物线与x轴有两个交点
7.（4分）如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E.若△CDE的周长为10，则AB＋AD的值是( )
A.10B.15C.25D.30
8.（4分）将抛物线y=(x—2)2—8向左平移3个单位，向上平移5个单位，得到新抛物线为( )
A.y=(x+1)2−13B.y=(x−5)2−13C.y=(x−5)2−3D.y=(x+1)2−3
9.（4分）如果一次函数y=kx+k+1的图象经过一、二、四象限，则k的取值范围是( )
A.k>−1B.k<−1C.k<0D.−110.（4分）若α，β是方程x2+2x﹣2026=0的两个实数根，则α2+3α+β的值为( )
A.2024B.2026C.2028D.2022
11.（4分）如图，点A(0，4)，B(3，0)，且四边形ABCD为正方形，若直线l：y=kx+4与线段BC有交点，则k的取值范围是( )
A.k≤43B.﹣43≤k≤﹣17C.﹣43≤k≤﹣1D.﹣43≤k≤43
12.（4分）将二次函数y=x2−5x−6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象，若直线y=2x+b与这个新图象有4个公共点，则b的范围为( )
A.−734二、 填空题 （本题共计7小题，总分28分）
13.（4分）方程x2=x的根是_____
14.（4分）抛物线y=(x—2)2—3顶点坐标是 __________.
15.（4分）如图，直线y=−x+m与y=x+3的交点的横坐标为—2，则关于x的不等式
—x+m>x+3>0的取值范围是_____
16.（4分）点A(−3,y1)，B(2,y2)在抛物线y=(x+1)2上，则y1________y2.(填“>”，“<”或“=”)
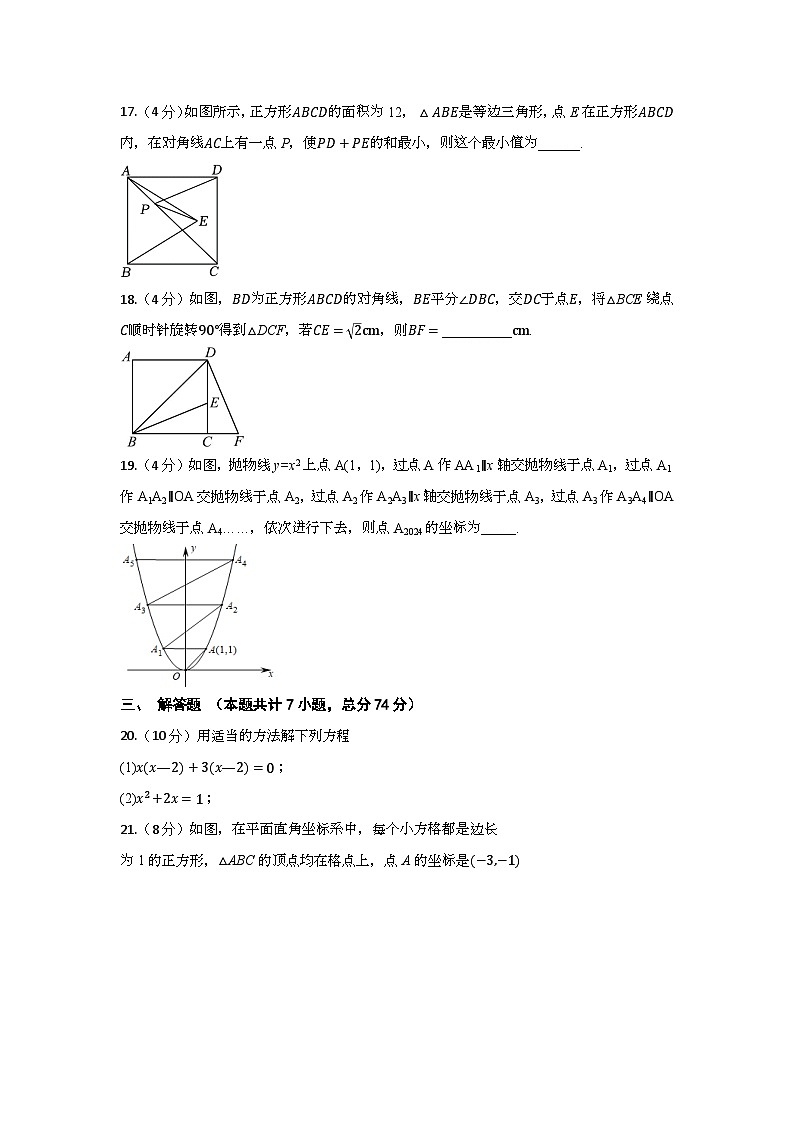
17.（4分）如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为______.
18.（4分）如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC于点E，将△BCE绕点C顺时针旋转90°得到△DCF，若CE=2cm，则BF=__________cm.
19.（4分）如图，抛物线y=x2上点A(1，1)，过点A作AA1∥x轴交抛物线于点A1，过点A1作A1A2∥OA交抛物线于点A2，过点A2作A2A3∥x轴交抛物线于点A3，过点A3作A3A4∥OA交抛物线于点A4……，依次进行下去，则点A2024的坐标为_____.
三、 解答题 （本题共计7小题，总分74分）
20.（10分）用适当的方法解下列方程
(1)x(x—2)+3(x—2)=0；
(2)x2+2x=1；
21.（8分）如图，在平面直角坐标系中，每个小方格都是边长
为1的正方形，△ABC的顶点均在格点上，点A的坐标是(−3,−1)
(1)将△ABC平移向上平移5个单位，向右4平移，
画出△ABC平移后△A1B1C1，则A1的坐标是________.
(2)画出△ABC绕坐标原点O逆时针旋转90°后的△A2B2C2，则A2的坐标是________.
22.（8分）某学校对八年级(1)、(2)两个班级的学生进行了一次数学测试，两个班级前5名的成绩(满分：100分)分别是：
八(1)班：92，86，85，85，77；
八(2)班：92，89，85，85，79.
两班的有关统计数据见下表.
请解决下面问题：
(1)a=________，b=________，c=________；
(2)根据统计数据表，说明哪个班级前5名的整体成绩较好.
23.（10分）如图，在矩形ABCD中，BD的垂直平分线分别交AB、CD、BD于E、F、O，连接DE、B F.
(1)求证：四边形BEDF是菱形；
(2)若AB＝8cm，BC＝4cm，求四边形DEBF的面积.
24.（12分）某商场以每件40元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于65元，经市场调查发现：该商品每天的销售量y(件)与每件售价x(元)之间满足一次函数y=−x+80的关系.
(1)当每件售价48元时，每天的利润是________元；
(2)销售这种商品，要想每天获利300元，每件商品的售价应为多少元？
(3)销售这种商品，每天是否能获利500元？为什么？
25.（12分）如图，在直角坐标系中，长方形纸片ABCD的边AB∥CO，点B坐标为(9,3)，若把图形按如图所示折叠，使B、D两点重合，折痕为EF.
(1)求证：△DEF为等腰三角形；
(2)求△ADE面积；
(3)求直线EF的函数表达式.
26.（14分）如图，在平面直角坐标系中，抛物线y=ax2+bx+c的顶点坐标为(2，9)，与y轴交于点A(0，5)，与x轴交于点E、 B.
(1)求二次函数y=ax2+bx+c的表达式
(2)过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点(点P在AC上方)，作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；
(3)若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边，求点M、N的坐标.
答案
一、 单选题 （本题共计12小题，总分48分）
1.（4分）【答案】C
2.（4分）【答案】C
3.（4分）【答案】C
4.（4分）【答案】B
5.（4分）【答案】A
6.（4分）【答案】D
7.（4分）【答案】A
8.（4分）【答案】D
9.（4分）【答案】D
10.（4分）【答案】A
11.（4分）【答案】B
12.（4分）【答案】A
二、 填空题 （本题共计7小题，总分28分）
13.（4分）【答案】x1=1，x2=0.
14.（4分）【答案】（2，-3）
15.（4分）【答案】—3 < x2 < —2 .
16.（4分）【答案】 <
17.（4分）【答案】23 .
18.（4分）【答案】2+22
19.（4分）【答案】(1013，10132)；
三、 解答题 （本题共计7小题，总分74分）
20.（10分）(1) x1=—3，x2=2 ；
(2) x 1=—1+2，x2=—1—2 ；
21.（8分）(1)图略，(1，4)；
(2)图略，(1，—3)；
22.（8分）(1)86， 85 ，85；
(2) 八(2)班的成绩较好
23.（10分）(1)∵四边形ABCD是矩形，O是BD的中点，
∴∠A＝90°，AD＝BC＝4，AB∥DC，OB＝OD，
∴∠OBE＝∠ODF
在△BOE和△DOF中，∴△BOE≌△DOF(ASA)，
∴EO＝FO，且OB＝OD
∴四边形BEDF是平行四边形，
∵EF垂直平分BD ∴BE＝DE
∴四边形BEDF是菱形
(2)∵四边形BEDF是菱形 ∴BE＝DE，
在Rt△ADE中，DE2＝AE2+DA2，
∴BE2＝(8﹣BE)2+16， ∴BE＝5
∴四边形DEBF的面积＝BE×AD＝20cm2.
24.（12分）(1)解：当每件售价48元时，销售量y=−48+80=32，
每天的利润=(48−40)×32=256(元)， 故答案为：256；
(2)解：根据题意可得：(x−40)(−x+80)=300，
整理得：x2+120x+3500=0，解得：x1=50,x2=70(舍去)，
答：每件商品的售价应为50元；
(3)解：根据题意可得：(x−40)(−x+80)=500，整理得：x2+120x+3700=0，
配方得：(x+60)2=−100<0，
∴该方程无解，
∴每天不能获利500元
25.（12分）(1)证明：由折叠得∠DEF=∠BEF，
∵AB∥CO，
∴∠BEF=∠DFE，
∴∠DEF=∠DFE，
∴△DEF为等腰三角形；
(2)∵点B的坐标为(9,3)，四边形ABCD为矩形，
∴AD=BC=3，CD=AB=9设点E的坐标为(x,3)，
∵DE=BE，∴AE=x，BE=9−x，
在Rt△AOE中，AE2+AO2=OE2，∴x2+32=(9−x)2，解得x=4，
∴E(4,3)∴AE=4，
∴三角形ADE面积=12AD⋅AE=12×3×4=6；
(3)∵AE=4，AD=3，∠A=90°∴OE=AD2+AE2=5
∴OF=OE=5 ∴F(5,0)，
设直线EF的解析式为y=kx+b，将E(4,3)，F(5,0)代入得，
{4k+b=35k+b=0，解得{k=−3b=15，
∴直线EF的解析式为y=−3x+15.
26.（14分）(1)y=−x2+4x+5
【解析】设抛物线解析式为y=a(x−2)2+9
∵抛物线与y轴交于点A（0，5）
∴4a+9=5，∴a=﹣1， y=﹣(x−2)2+9=−x2+4x+5
(2)点P(52，354)时，S四边形APCD最大=252；
【解析】当y=0时，-x2+4x+5=0，
∴x1=﹣1，x2=5， ∴E(﹣1，0)，B(5，0)，
设直线AB的解析式为y=mx+n，∵A(0，5)，B(5，0)，∴m=﹣1，n=5，
∴直线AB的解析式为y=﹣x+5；设P(x，﹣x2+4x+5)， ∴D(x，﹣x+5)，
∴PD=-x2+4x+5+x﹣5=-x2+5x， ∵AC=4，
∴S四边形APCD=12×AC×PD=2(-x2+5x)=-2x2+10x，
∴当x=10−2×(−2)=52时， ∴S四边形APCD最大=252，
(3)当M点的坐标为(1，8)时，N点坐标为(2，13)，当M点的坐标为(3，8)时，N点坐标为(2，3).
【解析】如图，
过M作MH垂直于对称轴，垂足为H，
∵MN∥AE，MN=AE，
∴△HMN≌△AOE，
∴HM=OE=1，
∴M点的横坐标为x=3或x=1，
当x=1时，M点纵坐标为8，当x=3时，M点纵坐标为8，
∴M点的坐标为M1(1，8)或M2(3，8)，
∵A(0，5)，E(﹣1，0)，
∴直线AE解析式为y=5x+5，
∵MN∥AE，
∴MN的解析式为y=5x+b，
∵点N在抛物线对称轴x=2上，
∴N(2，10+b)，
∵AE2=OA2+0E2=26 ∵MN=AE ∴MN2=AE2，
∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1，8)或M2(3，8)，
∴点M1，M2关于抛物线对称轴x=2对称，
∵点N在抛物线对称轴上，
∴M1N=M2N， ∴1+(b+2)2=26， ∴b=3，或b=﹣7，
∴10+b=13或10+b=3
∴当M点的坐标为(1，8)时，N点坐标为(2，13)，
当M点的坐标为(3，8)时，N点坐标为(2，3)
综上所述：当M点的坐标为(1，8)时，N点坐标为(2，13)，当M点的坐标为(3，8)时，N点坐标为(2，3).