广东省梅州市五华县2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份广东省梅州市五华县2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含广东省梅州市五华县2023-2024学年七年级下学期期中数学试题原卷版docx、广东省梅州市五华县2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

（全卷满分120分，检测时间120分钟）
一、选择题：本大题共10小题，每小题3分，满分30分．在每小题列出的四个选项中只有一个是符合题目要求的．请把答案填在下表里．
1. 下列各式中，计算结果等于a5的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题主要考查合并同类项，积的乘方，同底数幂相除，掌握运算法则是解题的关键．
【详解】解：A. 与不是同类项，不能合并，选项错误，不符合题意；
B. ，选项错误，不符合题意；
C. ，选项正确，符合题意；
D. ，选项错误，不符合题意．
故选：C．
2. “墙角数枝梅，凌寒独自开．遥知不是雪，为有暗香来．”出自宋代诗人王安石的《梅花》．梅花的花粉直径约为，用科学记数法表示该数据为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据科学记数法的表示方法，即可求解，
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，解题的关键是确定的值以及的值．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．
【详解】解：，
故选：B．
3. 如图，一条公路的两侧铺设了两条平行管道和，如果公路一侧铺设的管道与纵向连通管道的夹角为，那么公路另一侧铺设的管道与纵向连通管道的夹角的度数是（ ）
A B. C. D.
【答案】C
【解析】
【分析】本题考查了平行线的性质，两直线平行，同旁内角互补，列式代入数值，进行计算，即可作答．
【详解】解：∵两条平行管道和，
∴
∴
则
故选：C
4. 两条直线被第三条直线所截，形成了常说的“三线八角”，为了便于记忆，同学们可用双手表示“三线八角”（两大拇指代表被截直线，两只食指在同一直线上代表截线），如图，它们构成的一对角可以看成（ ）
A. 同位角B. 同旁内角C. 内错角D. 对顶角
【答案】A
【解析】
【分析】本题考查了同位角、内错角、同旁内角的识别，两条线a、b被第三条直线c所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角；两个角分别在截线的异侧，且夹在两条被截线之间，具有这样位置关系的一对角互为内错角；两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角，据此作答即可．
【详解】解：根据同位角、内错角、同旁内角的概念，
可知它们构成的一对角可以看成是同位角，
故选：A．
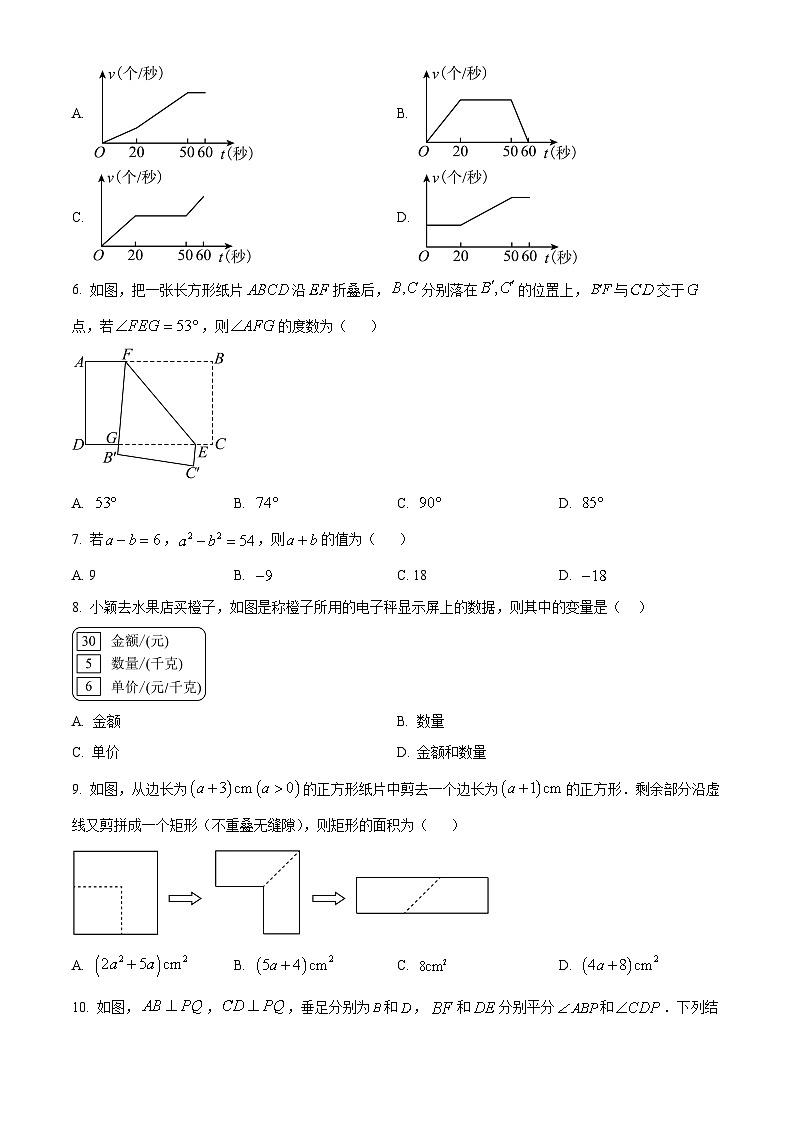
5. 实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加，后10秒冲刺，中间速度保持不变，则跳绳速度v（个/秒）与时间t（秒）之间的函数图象大致为（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】根据前20秒匀速，20秒至50秒保持跳绳速度不变，后10秒继续冲刺，分别得出速度v随时间t的增加的变化情况，即可求得．
【详解】首先前20秒匀速，则此时跳绳速度v随时间t增加而增加，即；
然后20秒至50秒保持跳绳速度不变，则此时跳绳速度v随时间t的增加而不变，即（a为常数）；
最后10秒冲刺，则此时跳绳速度v随时间t的增加而增加，即；
故选：C．
【点睛】本题考查一次函数的实际应用问题，理解题意是解题关键.
6. 如图，把一张长方形纸片沿折叠后，分别落在的位置上，与交于点，若，则的度数为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查的是平行线的性质以及折叠的性质，根据已知得出是解题关键．
首先根据得到，然后求出，进而求解即可．
【详解】∵，
∴
由折叠可得，
∴．
故选：B．
7. 若，，则的值为（ ）
A. 9B. C. 18D.
【答案】A
【解析】
【分析】根据平方差公式，即可求解，
本题主要考查了平方差公式，熟知平方差公式是解题的关键．
【详解】解：∵，，，
∴，
∴，
故选：．
8. 小颖去水果店买橙子，如图是称橙子所用电子秤显示屏上的数据，则其中的变量是（ ）
A. 金额B. 数量
C. 单价D. 金额和数量
【答案】D
【解析】
【分析】本题考查变量与常量，根据变化的量叫变量，恒定不变的量叫常量逐个判断即可得到答案；
【详解】解：由题意可得，
金额单价数量，单价不变，数量与金额是变化的量，
∴单价常量，数量与金额是变量，
故选：D．
9. 如图，从边长为的正方形纸片中剪去一个边长为的正方形．剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（ ）
A B. C. D.
【答案】D
【解析】
【分析】根据题意列出矩形的长和宽，根据面积公式，即可求解，
本题考查了列代数式，整式乘法，解题的关键是：列出长方形的长和宽．
【详解】解：由题意得：矩形的长为：，矩形的宽为：，则矩形的面积为：，
故选：D．
10. 如图，，，垂足分别为和，和分别平分和．下列结论：①；②；③；④．其中结论正确的序号是（ ）
A. ①②③B. ②③④C. ①②④D. ③④
【答案】C
【解析】
【分析】由，，得到，可判断①，由和分别平分和，，，可得，可判断②，进而得到，，可判断④，由不一定平行，可判断③
本题考查了平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键.
【详解】解：∵，，
∴，故①正确，
∵和分别平分和，，，
∴，，
∴，故②正确，
∴，
∴，故④正确，
∵不一定平行，
∴不一定垂直故③不正确，
故①②④正确，③错误，
故选：C．
二、填空题：本大题共6小题，每小题3分，满分18分．请将答案填入试题对应位置．
11. 已知一个角是，则这个角的余角的度数是______度．
【答案】70
【解析】
【分析】本题考查了余角的定义，掌握互余的两个角和为是解此题的关键．根据余角的定义可直接进行求解．
【详解】解∶∵一个角是，
∴这个角的余角的度数是，
故答案为∶70．
12. 某商场利用“五一”开展促销活动：一次性购买某品牌服装件，每件仅售元，如果超过件，则超过部分可享受折优惠，顾客所付款（元）与所购服装件之间的函数解析式为__________．
【答案】
【解析】
【分析】因为所购买的件数x≥3，所以顾客所付款y分成两部分，一部分是3×80=240，另一部分是（x-3）×80×0.8，让它们相加即可．
【详解】解：∵x≥3，
∴y=3×80+（x-3）×80×0.8=64x+48（x≥3）．
故答案是：.
【点睛】此题主要考查利用一次函数解决实际问题，找到所求量的等量关系是解决问题的关键．
13. 若，，则的值是______．
【答案】35
【解析】
【分析】根据同底数幂乘法的逆用进行计算即可，
本题考查了同底数幂乘法的逆运算，熟练掌握法则是解答本题的关键．
【详解】解：，
故答案为：35．
14. 如图是路灯维护工程车的工作示意图，工作篮底部与支撑平台平行．若，则的度数为______．

【答案】
【解析】
【分析】过顶点做直线支撑平台，直线将分成两个角，根据平行的性质即可求解．
【详解】解：过顶点做直线支撑平台，
支撑平台工作篮底部，
、，
，
，
．
【点睛】本题考查平行线的性质，熟练掌握平行线的性质是解题的关键．
15. 若，则______．
【答案】
【解析】
【分析】本题考查了多项式乘以多项式， 把等于号右边的式子展开，再合并同类项，利用等于号对应的性质，可得关于a、b的方程，即可求解．
【详解】解：
，
∴，，
∴，
故答案为：．
16. 如图，点是线段上一点，以为边向两边作正方形，面积分别是和，设，两个正方形的面积之和，则的面积为______．
【答案】5
【解析】
【分析】本题主要考查了完全平方公式在几何图形中的应用，设，，则由题意得，，，然后根据进行求解即可．熟知完全平方公式是解题的关键．
【详解】解：设，，
∴，，
则，
∴．
故答案为：5．
三、解答题：本大题共9小题，满分72分，解答要求写出文字说明、证明过程或计算步骤．
17. 计算：．
【答案】．
【解析】
【分析】此题考查了实数的混合运算，先进行有理数的乘方，负整数次幂和化简绝对值，再计算乘法，最后加减即可，熟练掌握运算法则是解题的关键．
【详解】解：原式，
，
．
18. 某同学计算一个多项式除以时，得到的答案是．请你帮该同学求出这个多项式．
【答案】
【解析】
【分析】本题考查了整式的混合运算，根据被除数＝除数×商，计算即可得到结果．
【详解】解∶
19. 一个角的补角加上，恰好等于这个角的5倍，求这个角的度数．
【答案】这个角的度数为．
【解析】
【分析】本题主要考查了补角，一元一次方程的应用，熟练掌余角和补角的定义进行求解是解决本题的关键．
设这个为，则这个角的补角为，根据题意可列等式，求解即可得出答案．
【详解】解：设这个角为，则这个角的补角为，
根据题意可得，，
解得：，
这个角的度数为．
20. 先化简，再求值：，其中，．
【答案】，13
【解析】
【分析】本题主要考查了整式的化简求值，正确化简整式是解题关键．首先将括号里面进行运算，进而利用整式混合运算法则化简，再把已知数代入求出答案．
【详解】解∶
，
当，时，原式．
21. 如图，在中，已知，点在边上．
（1）尺规作图（保留作图痕迹，不必写作法）以为顶点，为一边作，交于．
（2）在（1）的条件下，求的度数．
【答案】（1）见解析 （2）
【解析】
【分析】本题考查了复杂作图，平行线的判定与性质等知识，解题的关键是∶
（1）根据作一个角等于已知角的作法作即可；
（2）根据“同位角相等，两直线平行”得出，然后利用平行线的性质求解．
【小问1详解】
解∶如图，即为所求，
【小问2详解】
解：由作图知：，
∴，
∴，
又，
∴．
22. 丘成桐祖居位于广东省梅州市蕉岭县文福镇白湖村东面的羊岃村．明成化年间（年），八世祖惟述丘公开基建业，迄今500余年，是国家级旅游景区．2024年“清明”期间，小明和父母一起开车从梅州五华出发到距家150千米的丘成桐祖居旅游．出发前，汽车油箱内还有油20升，当行驶100千米时，发现油箱余油量为10升（假设行驶过程中汽车的耗油量是均匀的）．
（1）该车平均每千米的耗油为______升，在保证油箱有油的情况下，行驶路程（千米）与剩余油量（升）的关系式______．
（2）当汽车到达丘成桐祖居时，求剩余油量的值；
（3）当油箱中剩余油量低于4升时，汽车仪表盘油灯将自动报警，中途至少要加多少升油才能够在汽车仪表盘油灯不报警的情况下把车开回家．
【答案】（1）；
（2）剩余油量的值为
（3）至少要加升油
【解析】
【分析】（1）由题意列式计算即可得出该车平均每千米的耗油，从而得出关系式，
（2）将代入，即可求解，
（3）算出往返耗油量，根据题意列式，即可求解，
本题考查了列代数式、求代数式的值、有理数的混合运算的应用，理解题意，正确得出关系式，列出式子进行计算是解此题的关键．
【小问1详解】
解：根据题意得：（升），
在保证油箱有油的情况下，行驶路程（千米）与剩余油量（升）的关系式，
故答案为：，，
【小问2详解】
解：将代入，得：（升），
故答案为：剩余油量的值为，
【小问3详解】
解：由题意得，往返一共需要油：（升），
∵油箱中剩余油量低于4升，汽车仪表盘油灯将自动报警，
∴中途加油量为：（升），
故答案为：至少要加升油．
23. 如图，平分，且与线段相交于点是上一点，连接．若，，
（1）请说明；
（2）请判断与的位置关系，并说明理由．
【答案】（1）见解析 （2），理由见解析
【解析】
【分析】本题考查了平行线的判定与性质，解题的关键是：
（1）利用角平分线的定义，并结合，可证明，然后利用平行线的判定即可得证；
（2）利用平行线的性质得出，利用补角的性质可得出，然后利用平行线的判定即可得出结论．
【小问1详解】
证明∶∵平分，
∴，
∵，
∴，
∴；
【小问2详解】
解：
理由：
∵，
∴，
又
∴，
∴．
24. 龙年春晚首次在演播大厅部署了沉浸式舞台交互系统，现场观众可以看到李白带你云游长安、大熊猫花花上春晚教学八段锦…与的技术融合让人耳目一新，淇淇同学深受智能技术触动，发明了一个智能关联盒．当输入数或式时，盒子会直接加4后输出．
（1）第一次淇淇输入为，则关联盒输出为 ；若关联盒第二次输出为，则淇淇输入的是 ；
（2）在（1）的条件下，若把第一次输入的式子作为长方形甲的宽，输出的式子作为长，其面积记作，把第二次输入的式子作为长方形乙的宽，输出的式子作为长，其面积记作．
①请用含n的代数式分别表示和（结果化成多项式的形式）；
②淇淇发现可以化为一个完全平方式，请解释说明．
【答案】（1），
（2）①，；②说明见解析
【解析】
【分析】本题考查整式计算，多项式乘多项式，合并同类项，完全平方公式．
（1）根据题意利用整式计算即可；
（2）①根据题意分别表示出和代数式再化简即可；②利用完全平方公式定义即可．
【小问1详解】
解：由题意得：
第一次淇淇输入为，则关联盒输出为：，
关联盒第二次输出为，则淇淇输入的是：，
故答案为：，；
【小问2详解】
解：①，；
②，
∵，
∴可以化为一个完全平方式．
25. 【动手实践】
在数学研究中，观察、猜想、实验验证、得出结论，是我们常用的几何探究方式．
请你利用一副含有角的直角三角板和含有角的直角三角板尝试完成探究．
【实验操作】
（1）如图1，当边和边重合时，______度；
（2）如图2，保持三角板不动，将角的顶点与三角板的角的顶点重合，然后摆动三角板，当是多少度时，？请说明理由；
【拓展延伸】
（3）如图3，试探索：保持三角板不动，将角的顶点与三角板的角的顶点重合，然后摆动三角板，使得与中其中一个角是另一个角的两倍，请直接写出所有满足题意的的度数．
【答案】（1）（2）或（3）为或或或
【解析】
【分析】（1）由角的和差关系可得答案，
（2）分两种情况画出图形，再利用角的和差运算可得答案，
（3）分四种情况分别画出图形，再结合角的和差运算可得答案，
本题考查的是角的和差运算，熟练的画出图形，清晰的分类讨论是解本题的关键．
【详解】解：（1）∵，，
∴，
故答案为：105；
（2）如图，
∵，，即：，
∴，
如图，
∵，
∴，
综上，当或时，；
（3）如图，
∵，，
∴，
∴，
如图，
∵，，
∴，
∴，
如图，
∵，，
∴，
∴，
如图，
∵，，
∴，
∴，
综上，为或或或．