广东省阳江市2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份广东省阳江市2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含广东省阳江市2023-2024学年七年级下学期期中数学试题原卷版docx、广东省阳江市2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

七年级数学
本试卷共4页，24小题，满分120分．考试用时120分钟．
注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的学校、姓名和准考证号填写在答题卡上．
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．
4．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．
一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 下列实数中，是无理数的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．根据定义逐一分析判断即可．
【详解】解： ∵，
∴，，是有理数，是无理数，
故选B．
2. 算术平方根是（ ）
A. B. 5C. 5或D. 25
【答案】B
【解析】
【分析】本题考查的是“算术平方根”的定义：“对于一个非负数x，若，则x叫做a的算术平方根”是解答本题的关键． 根据“算术平方根”的定义进行分析判断即可．
【详解】解：∵，
∴的算术平方根是5．
故选B．
3. 如图，某地进行城市规划，在一条新修公路MN旁有一村庄P，现要建一个汽车站，且有A，B，C，D四个地点可供选择．若要使汽车站离村庄最近，则汽车站应建在（ ）
A. 点A处B. 点B处C. 点C处D. 点D处
【答案】C
【解析】
【分析】根据垂线段最短解答即可．
【详解】解：根据垂线段最短可知建在点C处，汽车站离村庄最近，
故选：C．
【点睛】本题考查了垂线的性质，熟练掌握垂线的性质是解答本题的关键．经过一点有且只有一条直线与已知直线垂直，连接直线外一点与直线上各点的所有线段中，垂线段最短．
4. 已知，则以下对的估算正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了无理数的估算，用夹逼法估算无理数的大小即可得出答案．
【详解】解：∵，
∴，
∴，即，
∴，
故选：B．
5. 在平面直角坐标系中，若点在第二象限，则m可能是（ ）
A. B. 0C. D. 2
【答案】D
【解析】
【分析】本题主要考查点所在象限，先根据第二象限内点的坐标符号特点确定m的正负，然后结合各选项即可解答．掌握第二象限的点的横坐标小于零、纵坐标大于零是解题的关键．
【详解】解：∵点第二象限，
∴，
∴A、B、C选项不符合题意，D选项符合题意．
故选：D．
6. 如图是小明探索直线平行的条件时所用的学具，木条，，在同一平面内．经测量，，要使木条，则的度数为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了对顶角相等的性质和平行线的判定，熟练掌握平行线的判定条件是解题的关键．根据同旁内角互补，两直线平行可求出，再根据对顶角相等解答．
【详解】解：如图，
∵要使，则，
．
∴，
故选：．
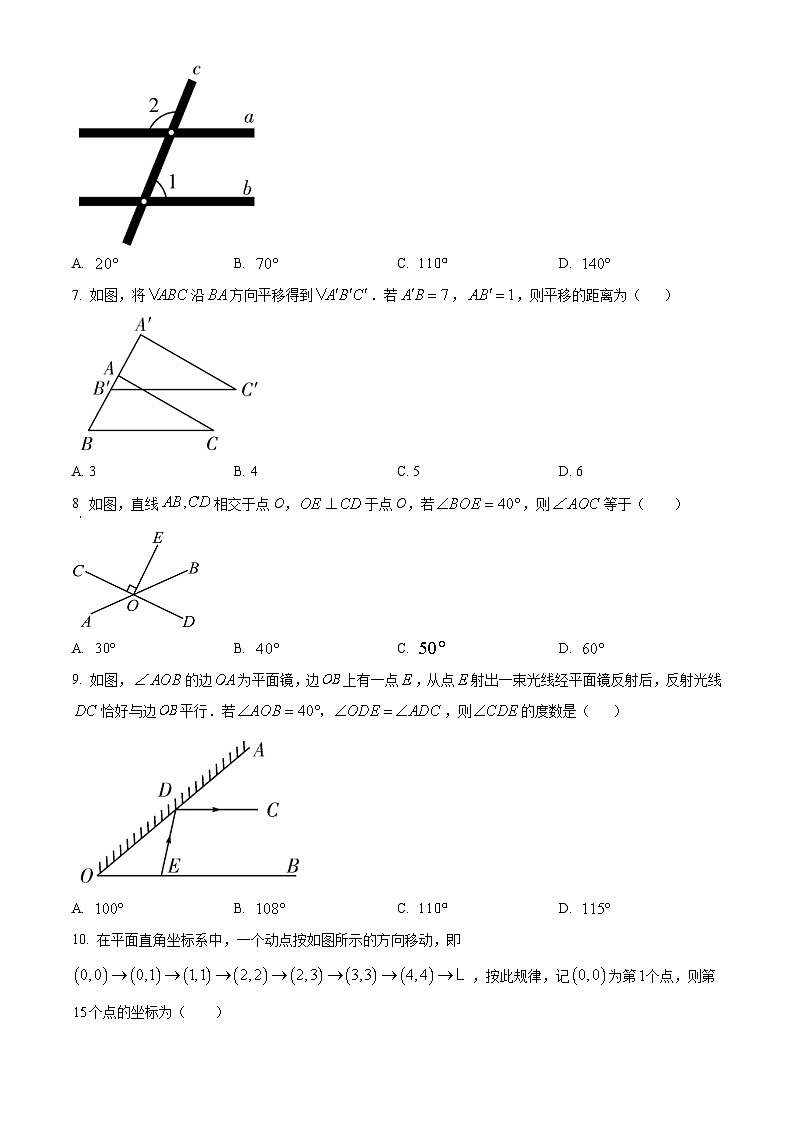
7. 如图，将沿方向平移得到．若，，则平移的距离为（ ）
A. 3B. 4C. 5D. 6
【答案】A
【解析】
【分析】本题考查了平移的性质，主要利用了对应顶点的连线的长度等于平移距离．根据平移的性质解答即可．
【详解】解：∵将沿方向平移得到，
∴
∵，，，
∴平移距离为，
故选：A．
8. 如图，直线相交于点O，于点O，若，则等于（ ）
A. B. C. D.
【答案】C
【解析】
【分析】应用垂线的性质及对顶角的定义进行计算即可得出答案．
【详解】解：，
，
，
，
，
故选：C．
【点睛】本题考查了垂线、对顶角，熟练掌握垂线的性质及对顶角的定义进行求解是解题的关键．
9. 如图，的边为平面镜，边上有一点，从点射出一束光线经平面镜反射后，反射光线恰好与边平行．若，则的度数是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查了平行线性质．解答本题的关键是根据题意找到法线，然后由法线的性质来解答问题，此题属跨学科题目．
过点作交于点．根据题意知，是的角平分线，故；然后又由两直线推知内错角；最后由三角形的内角和定理求得的度数，即可求得，最后由求解．
【详解】解：过点作交于点．
∵，
，
，
（两直线平行，内错角相等）；
（等量代换）；
在中，，，
；

∴．
故选：A．
10. 在平面直角坐标系中，一个动点按如图所示的方向移动，即，按此规律，记为第个点，则第个点的坐标为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了坐标规律的探究，先由题意写出前几个点的坐标，观察发现并归纳：横坐标与纵坐标相等且为奇数的点的坐标特点，从而可得答案，解题的关键是仔细观察坐标变化规律，掌握从具体到一般的探究方法．
【详解】解：∵，
∴观察发现，每三个点为一组，每组最后一个点的坐标为，
∵，
∴第个点的坐标为第五组最后一个点的坐标，
∴第个点的坐标为，
故选：．
二、填空题：本大题共6小题，每小题3分，共18分．
11. 比较大小：___________4（填“”、“”或“”）．
【答案】
【解析】
【分析】被开方数越大，则这个实数越大，据此即可作答．
【详解】∵，
∴，
故答案为：．
【点睛】本题主要考查了实数大小的比较，属于基础题，细心计算是解答本题的关键．
12. 要说明命题“若a＜1，则a2＜1”是假命题，可以举的反例是a＝________（一个即可）
【答案】−2（答案不唯一，满足题意即可）
【解析】
【分析】要使得a2<1成立，则−1【详解】解：由题意，当a=−2时，满足a<1，但不满足a2<1，
故答案为：−2（答案不唯一，满足题意即可）．
【点睛】本题考查命题的判断，以及不等式的性质，理解命题的定义，能够根据命题适当的举出反例是解题关键．
13. 已知和是实数x的两个平方根，则x的值是_______．
【答案】4
【解析】
【分析】本题考查了平方根，根据一个正数有两个平方根，且它们互为相反数即可求出m的值，从而求出x的值．
【详解】∵和是实数x的两个平方根，
∴，
解得，
∴，，
∴，
故答案为：4．
14. 在平面直角坐标系内，把点P（－5，－2）先向左平移3个单位长度，再向上平移2个单位长度后得到的点的坐标是 ____________．
【答案】（－8，0）
【解析】
【分析】向左平移3个单位长度则横坐标减3，向上平移2个单位长度则纵坐标加2，由此可得答案．
【详解】把点P（－5，－2）先向左平移3个单位长度，再向上平移2个单位长度后得到（－8，0），
故答案为：（－8，0）．
【点睛】本题考查坐标系中点的平移，熟记左右平移改变横坐标，上下平移改变纵坐标是解题的关键．
15. 若x，y为实数， 且 ，则________．
【答案】
【解析】
【分析】本题主要考查非负数的性质，几个非负数的和为0，则每一个非负数同时为0．利用非负数的性质得到，，然后求出代数式的值．
【详解】解：∵，
∴，，
∴，，
∴；
故答案为：．
16. 如图，若直线，，，则______．
【答案】##40度
【解析】
【分析】本题主要考查了三角形的外角定理以及平行线的性质，解题的关键是掌握“三角形的一个外角定于与它不相邻的两个内角之和”，“两直线平行，同旁内角互补”．根据三角形的外角定理可得，，再根据平行线的性质可得，即可求解．
【详解】解：根据题意可得：
，，
∴，
∵，
∴，
∴，
故答案为：．
三、解答题（一）：本大题共3小题，第17题10分，第18、19题各7分，共24分．
17. 计算：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题考查的是实数的混合运算，掌握运算顺序是解本题的关键；
（1）先计算括号内运算，再计算乘方，再乘除，最后计算加减运算即可；
（2）先计算乘方，算术平方根，立方根，绝对值，再合并即可．
小问1详解】
解：原式．
【小问2详解】
原式．
18. 如图1，杆秤是利用杠杆原理来称质量的简易衡器．如图2是杆秤的示意图，，经测量，，，请判断与的位置关系，并说明理由．
【答案】，理由见解析
【解析】
【分析】本题主要考查了平行线的性质、平行线的判定等知识点，掌握两直线平行、同旁内角互补；内错角相等、两直线平行是解答本题的关键．根据平行线的性质及，得,再根据内错角相等、两直线平行即可解答．
【详解】解：．理由如下：
，
．
．
．
．
19. 如图，在平面直角坐标系中，的顶点都在网格点上，其中点的坐标是．
（1）点的坐标是______，点的坐标是______；
（2）将先向左平移2个单位长度，再向上平移1个单位长度后，得到．请画出，并直接写出点的坐标．
【答案】（1）；
（2）画图见解析；
【解析】
【分析】本题考查的是坐标与图形，画平移图形，掌握平移的性质是解本题的关键．
（1）根据的位置可得其坐标；
（2）分别确定平移后的对应点，再顺次连接即可，再结合的位置可得其坐标；
【小问1详解】
解：根据的位置可得：；；
【小问2详解】
如图，即为所求作的三角形；
，
∴．
四、解答题（二）：本大题共3小题，每小题8分，共24分．
20. 已知6a+3的立方根是3，3a+b﹣1的算术平方根是4．
（1）求a，b的值；
（2）求b2﹣a2的平方根．
【答案】（1）4；5 （2）±3
【解析】
【分析】（1）运用立方根和算术平方根得出方程求解即可得；
（2）先求出代数式的值，然后计算平方根即可．
【小问1详解】
解：∵的立方根是3，的算术平方根是4，
∴，，
∴，；
【小问2详解】
解：由（1）知，，
∴，
∵9的平方根为，
∴的平方根为．
【点睛】本题考查了平方根、算术平方根、立方根及解方程，理解题意，根据题意得出方程是解题关键．
21. 在平面直角坐标系中，对于点，若点的坐标为，其中为常数，则称点是点的“倍相关点”．
例如，点的 “3倍相关点”的横坐标为：，纵坐标为：，所以点的 “3倍相关点”的坐标为．
（1）已知点的“倍相关点”是点，求的值；
（2）已知点的“倍相关点”是点，且点在轴上，求点到轴的距离．
【答案】（1）2 （2）
【解析】
【分析】本题考查了坐标与图形性质，“相关点”的定义，解题的关键是理解题意，理解“相关点”的运算．
（1）根据相关点的定义即可求解；
（2）先再根据点在轴上，得到其横坐标为0，即可求出的值，再根据相关点的定义求出点的纵坐标，进而求解；
【小问1详解】
解：点的横坐标为：，
点N的纵坐标为：，
∴；
【小问2详解】
解：∵点在轴上，
∴点的横坐标为0，
∵点是点的“倍相关点”，
∴，解得：，
∴点的纵坐标为：，
∴点的纵坐标为：，
∴点到轴的距离为．
22. 如图：已知，∠HCO＝∠EBC，∠BHC+∠BEF＝180°．
（1）求证：EFBH；
（2）若BH平分∠EBO，EF⊥AO于F，∠HCO＝64°，求∠CHO的度数．
【答案】（1）见解析 （2）58°
【解析】
【分析】（1）要证明，可通过与互补求得，利用平行线的性质说明可得结论；
（2）要求的度数，可通过平角和求得，利用（1）的结论及角平分线的性质求出及的度数即可．
【小问1详解】
证明：，
，
．
，
．
；
【小问2详解】
解：，
，
平分，
．
，，
，
．
．
【点睛】本题考查了平行线的性质和判定、角平分线的性质等知识点，理解题意学会分析是解决此类问题的关键．
五、解答题（三）：本大题共2小题，每小题12分，共24分．
23. 如图，已知直线，，点，在直线上，且满足，平分．
（1）求的度数．
（2）若左右平移，在平移的过程中：
①求与的比值；
②是否存在某种情况，使？若存在，求出的度数；若不存在，请说明理由．
【答案】（1）
（2）①；②存在，
【解析】
【分析】（1）由直线，根据两直线平行，同旁内角互补，即可求得的度数，又由，即可求得的度数；
（2）①首先由直线，根据两直线平行，同旁内角互补与两直线平行，内错角相等，可得，，由，进而可得，即可解答，②首先设，由直线，根据两直线平行，同旁内角互补与两直线平行，内错角相等，可求得与的度数，又由，即可得方程，解此方程即可求得答案．
【小问1详解】
解：，
．
，平分，
．
【小问2详解】
解：①，
，．
，
．
．
②设．
，
，
，
，
．
若，则．
解得，
存在．
【点睛】本题主要考查了平行线的性质，平行四边形的性质，角平分线的性质．解题的关键是注意掌握两直线平行，同旁内角互补与两直线平行，内错角相等定理的应用，注意数形结合与方程思想的应用．
24. 如图，已知，点，分别在直线，上，点是，之间的一个动点．
图1 图2 备用图
（1）如图1，当点在线段的左侧时，求证：．
（2）如图2，当点在线段的右侧时，，，之间的数量关系为______
（3）若，的平分线交于点，且，求的度数．
【答案】（1）见解析 （2）
（3）或
【解析】
【分析】（1）点P作直线，根据平行线性质及角度加减即可得到；
（2）点P作直线，根据平行线性质及角度加减即可得到；
（3）在（1）（2）的基础上作出图形，根据邻补角得到、的和，结合角平分线得到两半角之和，根据（2）的结论即可得到答案．
【小问1详解】
证明：过点P作直线，
得，
∵，
∴，
∴，
∵，
∴；
【小问2详解】
解：过点P作直线，
得，
∵，
∴，
∴，
∵，
∴，
∴，
故答案为：；
【小问3详解】
解：当点P在线段左侧时，如下图所示，
∵，，
∴，
∴；
当点P在线段右侧时，如下图所示，
∵，，
∴，
∴，
∴；
∴的度数为或．
【点睛】本题主要考查了平行线的性质，平行公理及推论等知识点：两条直线平行于第三条直线时，两条直线平行：两直线平行，内错角相等，同旁内角互补，作辅助线后能求出各个角的度数，是解此题的关键．