数学九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质教学演示课件ppt

这是一份数学九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质教学演示课件ppt，共19页。PPT课件主要包含了自主探究，小组讨论，向上平移，k个单位，k＞0，向下平移，-k个单位，k＜0，口决上加下减，小组展示等内容，欢迎下载使用。

请画出一次函数y=2x和y=2x+1的图象.观察你画出的图象，你发现这两个函数图象之间有什么关系？由此你能推测出二次函数y=x2和y=x2+1的图象之间有什么关系吗？
在边长为15 cm的正方形铁片中间剪去一个边长为x（cm）的小正方形铁片，剩下的贴片的面积y与x之间的函数关系式是什么？它的图象的顶点坐标是多少？
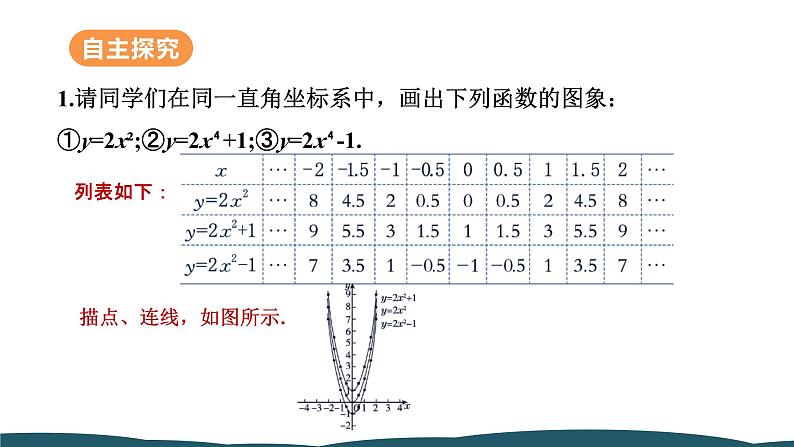
1.请同学们在同一直角坐标系中，画出下列函数的图象：①y=2x²;②y=2x⁴+1;③y=2x⁴-1.
2.请同学们在完成上面的任务后思考以下问题思考：①抛物线y=2x2+1和y=2x2-1的开口方向、对称轴和顶点坐标各是什么？ ②抛物线y=2x2+1，y=2x2-1与抛物线y=2x2有什么关系？
（抛物线y=2x2+1的开口向上，对称轴是y轴，顶点坐标是（0,1）；抛物线y=2x2-1的开口向上，对称轴是y轴，顶点坐标是（0,-1））
（把抛物线y=2x2向上平移一个单位长度得到抛物线y=2x2+1，向下平移一个单位长度得到抛物线y=2x2-1）
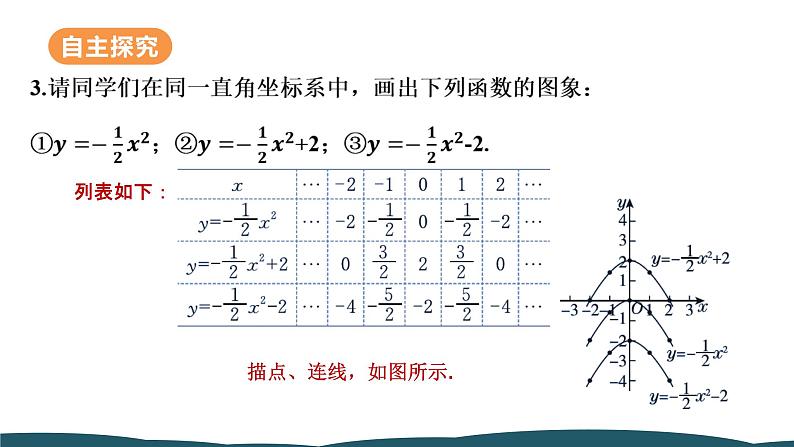
请你总结二次函数y=ax²+k的图象和性质.
当a>0时，图象开口向上；对称轴是y轴；顶点是(0,k),是抛物线的最低点；在对称轴左侧，y随x的增大而减小，在对称轴右侧，y随x的增大而增大；a的值越大，抛物线的开口越小.当a<0时，图象开口向下；对称轴是y轴；顶点是(0,k),是抛物线的最高点；在对称轴左侧，y随x的增大而增大，在对称轴右侧，y随x的增大而减小；a的值越小，抛物线的开口越小.函数y=ax²+k和y=-ax²+k的图象关于直线y=k对称
思考：抛物线y=ax2+k可以如何由抛物线y=ax2得到？
提疑惑：你有什么疑惑？
知识点 二次函数y=ax2+k的图象和性质（重、难点）
例1 二次函数y=x²+1的图象大致是（ ）
【题型一】二次函数y=ax2+k的图象和性质
例2 关于二次函数y=-2x2+1，下列说法错误的是（ ）A.图象开口向下 B.图象的对称轴为直线x=0C.函数的最小值为1 D.当x>1时，y随x的增大而减小
例3:已知二次函数y=ax²-a的图象经过点(-2,-9).(1)求这个函数的解析式，并写出函数图象的顶点坐标；(2)当x为何值时，该函数有最大(小)值?最大(小)值是多少?
解 ：(1)将x=-2,y=-9代入y=ax²-a,得4a-a=-9,解得a=-3,∴这个函数的解析式为y=-3x²+3,当x=0时，y=3,∴函数图象的顶点坐标为(0,3).
(2)∵a=-3<0,函数图象的顶点坐标为(0,3)∴当x=0时，该函数有最大值，最大值是3.
1.本节课我们一起学习了哪些知识？2.二次函数y=ax2+k的图象可以由二次函数y=ax2的图象怎样得到？
二次函数y=ax²+k的图象与性质；二次函数y=ax²+k与y=ax²的关系