北师大版七年级下册2 幂的乘方与积的乘方课文内容课件ppt

这是一份北师大版七年级下册2 幂的乘方与积的乘方课文内容课件ppt，共20页。PPT课件主要包含了学习目标，导入新课，新知探究，a2m，amn，典例精析，当堂练习，a3m，课堂小结等内容，欢迎下载使用。

1.理解并掌握幂的乘方法则;（重点）2.掌握幂的乘方法则的推导过程并能灵活运用.（难点）
am·an=am+n (m,n都是正整数）
同底数幂相乘，底数不变，指数相加.
am·an·ap=am+n+p(m,n,p都是正整数）
同底数幂的乘法法则的逆用：
am+n=am·an(m,n都是正整数).
地球、木星、太阳可以近似地看做是球体.木星的半径约是地球的10倍，它的体积约是地球的多少倍？
木星的半径约是地球的10倍,它的体积约是地球的103倍.
(102)3=102×102×102 =102+2+2 =106
问题：太阳的半径约是地球的102倍，它的体积约是地球的多少倍？
太阳的的体积约是地球的(102)3倍.
你知道(102)3等于多少吗?
（同底数幂的乘法法则）
(4)(am)n=　　　　　　 =　　 　　　　=　 . 
做一做：计算下列各式,并说明理由.(1)(62)4=　　　　×　　　　×　　　　×　　　　=　　　　; (2)(a2)3=　　　　·　　　　·　　　　=　　　　; (3)(am)2=　　　　·　　　　=　　　　; 
根据以上计算和推理，你能得到什么结论？
(am)n= amn　(m，n都是正整数）
幂的乘方，底数 ＿＿，指数＿＿.
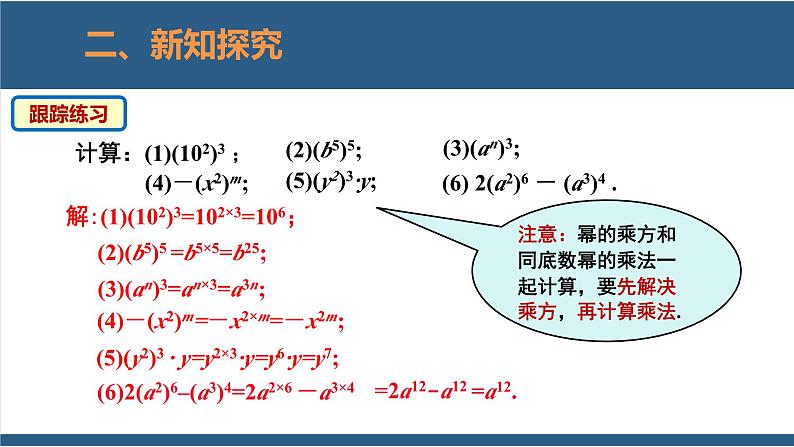
解:(1)(102)3=102×3=106；
(2)(b5)5 =b5×5=b25;
(6)2(a2)6–(a3)4=2a2×6 －a3×4
(5)(y2)3 · y=y2×3·y=y6·y=y7;
(3)(an)3=an×3=a3n;
(4)－(x2)m=－x2×m=－x2m;
注意：幂的乘方和同底数幂的乘法一起计算，要先解决乘方，再计算乘法.
做一做：（1）已知2x＋5y－3＝0，求4x·32y的值．
解：∵2x＋5y－3＝0，
∴4x·32y＝(22)x·(25)y ＝22x·25y＝22x＋5y＝23＝8.
底数不同，需要化成同底数幂，才能进行运算.
探究二：幂的乘方法则的应用
（2）已知3x=2,3y=3,求33x与32y的值.
解:33x=(3x)3=23=8.32y=(3y)2=32=9.
幂的乘方法则的逆用：amn=(am)n=(an)m
（2）-(b5)2=-b5×2=-b10.
（3）[(-a)4]3=(-a)12.
（4）(an+1)2=a2n+2.
（5）-[(m-n)5]3=-(m-n)15.
例2：计算下列各式.（1）(a2)3·(a3)2;　（2）(tm)2·t；（3）(x4)6-(x3)8.
解:（1）(a2)3·(a3)2=a2×3·a3×2=a6·a6=a12.
（2）(tm)2·t=t2×m·t=t2m+1.
（3）(x4)6-(x3)8=x4×6-x3×8=x24-x24=0.
先算幂的乘方,再算同底数幂的乘法,最后合并同类项.
例3：已知3m+4n-3=0,求8m×16n的值.
解:因为3m+4n-3=0,所以3m+4n=3,所以8m×16n=(23)m×(24)n =23m×24n =23m+4n=23=8.
1.计算(102)4的结果是(　　)A.106 B.108 C.109 D.105
2.下列运算正确的是(　　)A.a·a3=a3B.-(a2)3=a6C.(a3)2=a5D.2(a2)2-a4=a4
3.计算a3·(a3)2的结果是(　　)A.a8B.a9C.a11D.a18
5.如果正方体的棱长为(1-2b)3,那么这个正方体的表面积为(　　)A.(1-2b)6B.6(1-2b)6C.(1-2b)9D.6(1-2b)9
4.计算2(a2)6+(a3)4的结果是(　　)A.3a12D.以上都不对
8.计算:(1)-(x4)5;(2)[(-x)7]6; (3)-(x2n)3.
解:(1)原式=-x20.(2)原式=(-x)42.(3)原式=-x6n.
6.计算:(am)3=　　　　. 7.若x2n=4,则x8n=　　　　. 
9.计算:(1)(a2n-2)2·(an+1)3; (2)a3·a4·a+(a2)4+2(a4)2;(3)[(x+y)3]6+[(x+y)9]2; (4)[(b-3a)2]n+1·[(3a-b)2n+1]3.
解:(1)(a2n-2)2·(an+1)3=a2(2n-2)·a3(n+1)=a4n-4+3n+3=a7n-1.(2)原式=a8+a8+2a8=4a8.(3)[(x+y)3]6+[(x+y)9]2=(x+y)3×6+(x+y)9×2=(x+y)18+(x+y)18=2(x+y)18.(4)[(b-3a)2]n+1·[(3a-b)2n+1]3=(b-3a)2(n+1)·(3a-b)3(2n+1)=(3a-b)2n+2·(3a-b)6n+3=(3a-b)8n+5.
10.已知2x+3y-2=0,求9x×27y的值.
解:因为2x+3y-2=0,所以2x+3y=2,所以9x×27y=(32)x×(33)y=32x×33y=32x+3y=32=9.
解:因为2×8n×16n=215,所以21×23n×24n=21+3n+4n=215,则1+3n+4n=15,解得n=2.
11.若2×8n×16n=215,求n的值.