
(期中典型真题)专题5图形计算-江苏省苏州市2023-2024学年六年级下册数学期中高频易错核心考点(苏教版)
展开1.计算下面图形的体积。(单位:cm)
2.计算下面圆锥的体积。(单位:分米)
3.计算下面立体图形的体积:
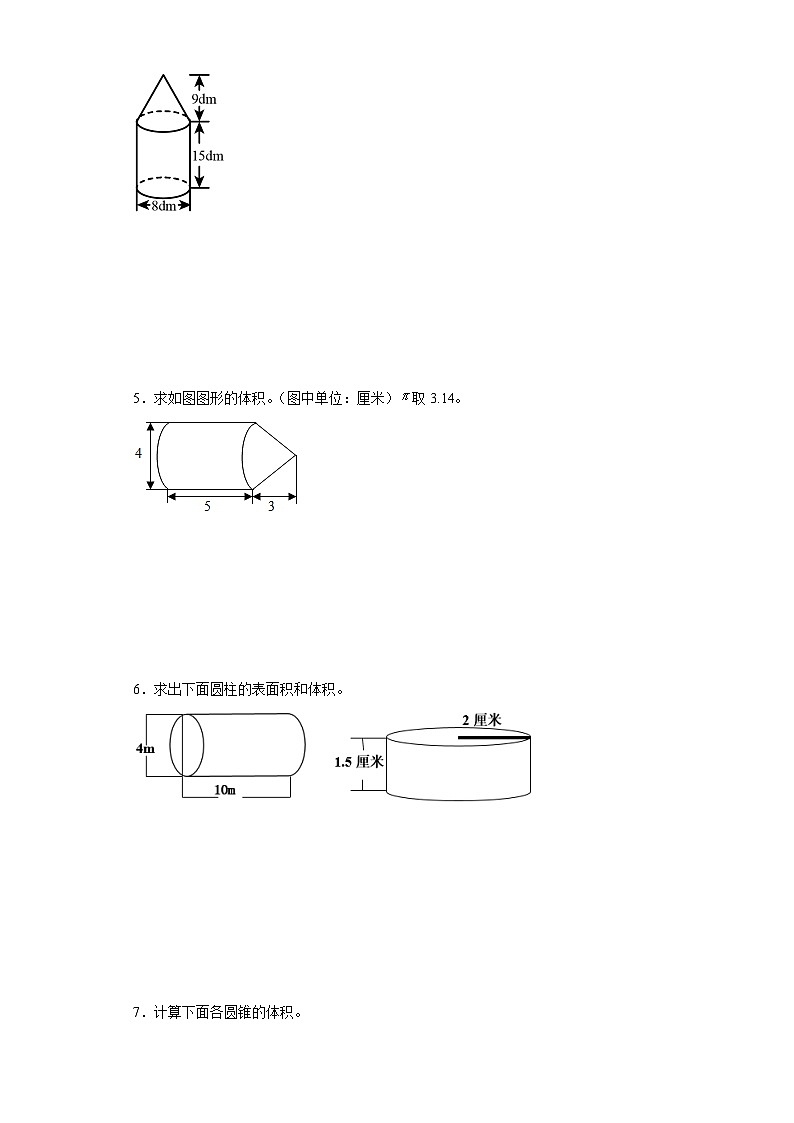
4.求下面图形的体积。
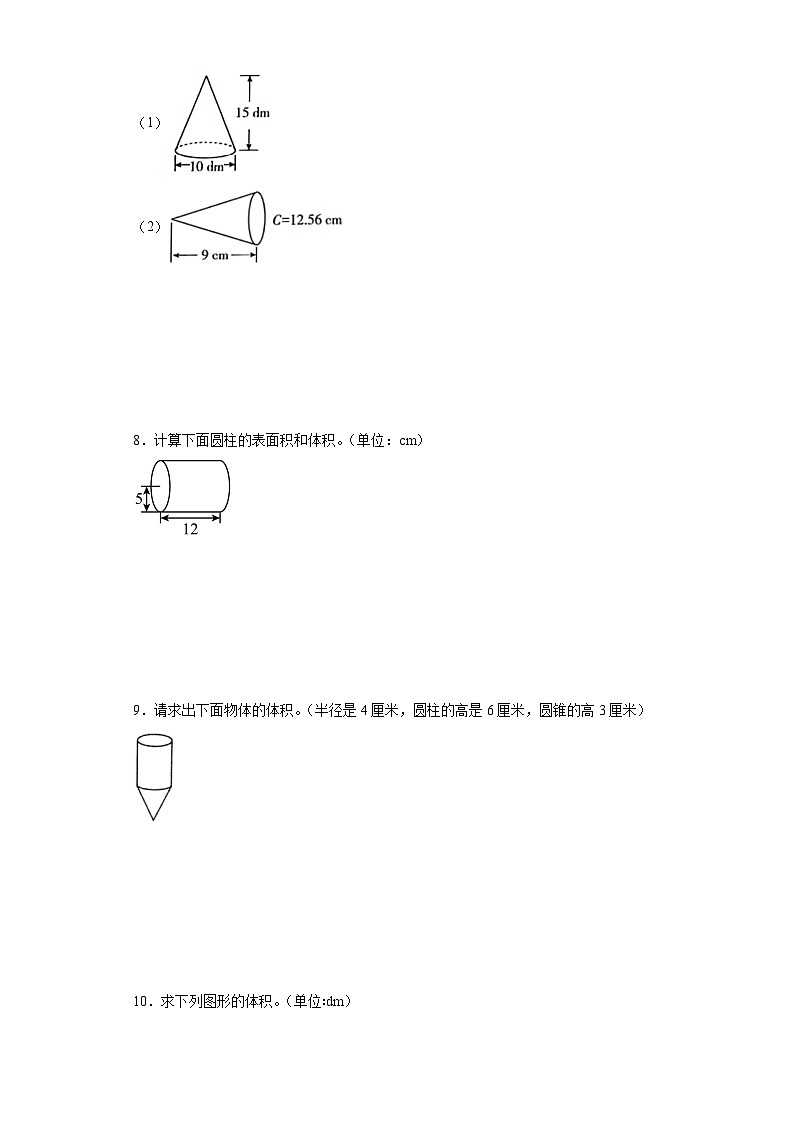
5.求如图图形的体积。(图中单位:厘米)取3.14。
6.求出下面圆柱的表面积和体积。
7.计算下面各圆锥的体积。
(1)
(2)
8.计算下面圆柱的表面积和体积。(单位:cm)
9.请求出下面物体的体积。(半径是4厘米,圆柱的高是6厘米,圆锥的高3厘米)
10.求下列图形的体积。(单位∶dm)
11.求阴影部分的面积。(单位:厘米)
12.计算下面各形体的底面积。(单位:厘米)
13.求圆锥的体积。
14.计算下面圆锥体的体积。(单位:分米 )
15.求下面圆柱的侧面积和体积。
16.求下列物体的体积。(单位:分米)
17.求下面圆柱的表面积。
18.求下面图形的体积。
19.求体积。
20.求下面圆柱的表面积,圆锥的体积.
21.求圆柱的表面积。(单位:厘米)
22.计算下面图形的面积和体积.
下图是一个直角梯形(单位:cm),如果以AB边为轴旋转一周,会得到一个立体图形.这个立体图形的底面积是多少?体积是多少?
23.将一面三角形小旗围绕小棒旋转一周,请计算出所得图形的体积。
24.计算圆锥的体积。(单位:分米)
25.计算圆柱的表面积。
26.求圆柱的表面积(单位:厘米)
27.求下面图形的表面积(单位:cm)。
28.求圆柱的表面积。(单位:厘米)
29.计算下面圆柱的表面积。(单位:分米)
30.计算下面各个圆柱的表面积。(单位:厘米)
31.计算下面圆柱的表面积。(单位:厘米)
32.求圆柱的表面积。(单位:厘米)
33.计算下图中圆柱的表面积和体积,圆锥的体积。
(1)
(2)
34.求下列立体图形的体积。
35.求下列立体图形的表面积和体积。(单位:cm)
36.求下列图形的体积.
37.下图是一个圆锥的侧面展开图,求这个圆锥的表面积。
38.计算如图所示的半圆模型的表面积。(π取3.14)
39.求下列圆柱的表面积和体积。
40.一个零件,如图,求它的体积.(π取3)
41.球球把一个直角三角形分别沿着它的两条直角边旋转一周,形成了两个圆锥,如图,请分别算出这两个圆锥的体积。
42.求下面图形的体积。
43.求下面圆锥的体积。h=4cm,r=3cm。
44.求下面各图形的表面积。(单位:cm)
45.求下面长方体的体积。
46.把下边的图形按比例放大后得到下面右边的图形,求未知数x。(单位:cm)
47.求下面各图形的体积。
48.求圆锥的体积。
49.计算下面图形的体积。(单位:厘米)
50.求下面每个图形的体积:(单位:厘米)
51.如图,把一根圆柱木料沿底面直径平均锯成两半。求这半个圆柱木料的表面积与体积。
52.求下列图形的体积.(单位:米)
53.计算表面积。(单位:厘米)
54.求如图所示的图形绕轴旋转一周后形成的物体的表面积。
55.求下面图形的表面积。(单位:厘米)
56.计算下面图形的体积。(单位:厘米)
57.按要求答题.
(1)计算图形1的表面积:
(2)计算立体图形2的体积.
参考答案:
1.251.2立方厘米;75.36立方厘米
【分析】根据圆柱体积公式:V=sh和圆锥体积公式V=sh,代入数据即可解答。
【详解】(1)3.14×4²×5
=50.24×5
=251.2(立方厘米)
(2)×3.14×3²×8
=9.42×8
=75.36(立方厘米)
2.150.72立方分米
【分析】先求出半径,根据圆锥体积=底面积×高×,列式计算即可。
【详解】
(立方分米)
3.282.6dm3
【详解】18.84÷3.14÷2=3(dm)
3.14×32×10=282.6(dm3)
4.904.32dm3
【分析】图形的体积=底面直径是8dm,高是15dm的圆柱的体积+底面直径是8dm,高是9dm的圆锥的体积;根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】3.14×(8÷2)2×15+3.14×(8÷2)2×9×
=3.14×16×15+3.14×16×9×
=50.24×15+50.24×9×
=753.6+452.16×
=753.6+150.72
=904.32(dm3)
5.75.36立方厘米
【分析】此图形事由直径为4厘米,高为5厘米的圆柱体和直径为4厘米高为3厘米的圆锥体组成的。圆柱体体积=,圆锥体体积=,圆的直径为4厘米,则半径为4÷2=2厘米,组合图形体积=圆柱体体积+圆锥体体积,代入数据计算即可。
【详解】×(4÷2)2×5+×(4÷2)2×3
=×22×5+×22×3
=×4×5+×4
=×20+4×
=(20+4)×
=24×
=24×3.15
=75.36(立方厘米)
即,组合图形体积是75.36立方厘米。
6.(1)150.72平方米;125.6立方米;(2)43.96平方厘米;18.84立方厘米
【分析】根据圆柱的表面积公式:和体积公式:即可解答。
【详解】(1)表面积:4×3.14×10+2×(4÷2)×3.14
=125.6+25.12
=150.72(平方米)
体积:3.14×(4÷2)×10
=12.56×10
=125.6(立方米)
(2)表面积:2×2×3.14×1.5+2×2×3.14
=18.84+25.12
=43.96(平方厘米)
体积:2×3.14×1.5
=12.56×1.5
=18.84(立方厘米)
此题主要考查学生对圆柱表面积和体积公式的应用。
7.(1)392.5cm;(2)37.68cm
【分析】(1)根据圆锥的体积V=sh=πr2h,把数值代入公式,解答即可;
先根据半径d=C÷π,在根据圆锥的体积V=sh=πr2h,把数值代入公式,解答即可。
【详解】(1)3.14×(10÷2)2×15×=392.5(cm3)
(2)12.56÷3.14=4(cm)
3.14×(4÷2)2×9×=37.68(cm3)
此题考查了圆锥的体积公式的计算应用,计算时不要漏掉。
8.533.8平方厘米;942立方厘米
【分析】直接运用圆柱表面积和体积公式代入数据计算即可。
【详解】表面积:3.14×5²×2+3.14×5×2×12
=157+376.8
=533.8(平方厘米)
体积:3.14×5²×12
=78.5×12
=942(立方厘米)
圆柱表面积和体积公式熟练运用为本题重点。
9.351.68立方厘米
【分析】根据圆柱体积公式:和圆锥体积公式,代入数值进行计算即可。
【详解】3.14×4×6+3.14×4×3×
=3.14×16×6+3.14×16×3×
=301.44+50.24
=351.68(立方厘米)
此题主要考查学生对组合图形的认识与求法,其中需要牢记圆锥和圆柱体积公式。
10.2512dm3
【分析】底面直径是20分米,那么底面半径是10分米,高是24分米,底面积乘高,再除以3得到圆锥的体积。
【详解】
(dm3)
11.平方厘米
【分析】观察图形可知,阴影部分面积=梯形面积-三角形面积-圆的面积的;根据梯形的面积公式:(上底+下底)×高÷2;三角形面积公式:底×高÷2;圆的面积公式:S=πr2;代入数据,即可解答。
【详解】(4+6)×(4+6)÷2-6×6÷2-3.14×42×
=10×10÷2-36÷2-3.14×16×
=100÷2-18-50.24×
=50-18-12.56
=32-12.56
=19.44(平方厘米)
12.(1)28.26平方厘米;(2)50.24平方厘米;(3)40平方厘米。
【分析】(1)圆柱的底面是一个圆,即求圆的面积,圆的面积公式:π×半径×半径;
(2)圆锥的底面是一个圆,即求圆的面积,圆的面积公式:π×半径×半径;
(3)长方体的底面是一个长方形,即求长方形的面积,长方形面积=长×宽。
【详解】(1)圆的半径:6÷2=3(厘米),
圆的面积:3.14×3×3
=3.14×9
=28.26(平方厘米)
(2)圆的半径:8÷2=4(厘米)
圆的面积:3.14×4×4
=3.14×16
=50.24(平方厘米)
(3)10×4=40(平方厘米)
此题考查的是圆柱、圆锥和长方体的特征,需熟练掌握圆的面积和长方形的面积公式才是解题关键。
13.25.12dm
【详解】根据圆锥的体积公式:V=r2h,把数据代入公式解答。
【解答】解:3.14×(4÷2)2×6
=3.14×4×6
=25.12(立方分米)
答:这个圆锥的体积是25.12立方分米。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
14.25.12立方分米
【分析】根据圆锥的体积V= πr2h,代入数据计算即可。
【详解】×3.14×22×6
=×12.56×6
=25.12(立方分米)
15.188.4cm²;282.6cm³
【分析】先根据圆的周长=直径×圆周率,计算出圆柱的底面周长,再根据圆柱的侧面积=圆柱的底面周长×高;圆柱的体积=底面积×高;据此解答。
【详解】侧面积:3.14×6×10
=18.84×10
=188.4(cm²)
体积:3.14×(6÷2)×10
=3.14×9×10
=282.6(cm³)
所以圆柱的侧面积为188.4cm²,体积为282.6cm³。
本题主要考查了圆柱的侧面积的体积的计算方法及其应用。圆柱的侧面是一个曲面,展开后是一个长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高,所以圆柱的侧面积等于底面周长乘高。
16.4710立方分米;1059.75立方分米
【分析】圆柱的体积=底面积×高;圆锥的体积=×底面积×高,据此解答。
【详解】3.14×102×15
=3.14×100×15
=4710(立方分米)
×3.14×(15÷2)2×18
=3.14×7.52×6
=1059.75(立方分米)
圆柱、圆锥的体积公式是解答此题的关键,注意计算时,要细心,不要出错。
17.635.85cm2
【分析】圆柱的表面积=底面积×2+侧面积;底面积=3.14×半径×半径,半径=直径÷2;侧面积=底面周长×高,底面周长=底面直径×3.14;代入数据即可求解。
【详解】3.14×2×2+3.14×9×18=635.85(cm2)
18.76.56cm3
【分析】观察图形可知,图形的体积=棱长是4cm的正方体的体积+底面直径是4cm,高是3cm的圆锥的体积,根据正方体体积公式:体积=棱长×棱长×棱长;圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】4×4×4+3.14×(4÷2)2×3×
=16×4+3.14×4×3×
=64+12.56×3×
=64+37.68×
=64+12.56
=76.56(cm3)
19.100.48立方厘米
【分析】根据圆锥体的体积公式:×底面积×高,代入数据,即可解答。
【详解】×3.14×(8÷2)2×6
=×3.14×16×6
=×50.24×6
=50.24×2
=100.48(立方厘米)
20.圆柱的表面积是207.24;圆锥的体积是58.875.
【详解】试题分析:根据圆柱的表面积=侧面积+底面积×2,圆锥的体积公式:v=Sh,把数据分别代入公式解答.
解:3.14×6×8+3.14×(6÷2)2×2
=18.84×8+3.14×9×2
=150.72+56.52
=207.24
答:这个圆柱的表面积是207.24.
×3.14×(5÷2)2×9
=3.14×6.25×3
=58.875
答:这个圆锥的体积是58.875.
【点评】此题主要考查圆柱的表面积公式、圆锥体积公式的灵活运用,关键是熟记公式.
21.282.6平方厘米
【分析】圆柱沿高展开后是两个圆和一个长方形,用这两个圆的面积+长方形的面积即可。
【详解】3.14×(6÷2)2×2+(24.84-6)×(6×2)
=56.52+18.84×12
=56.52+226.08
=282.6(平方厘米)
本题考查了圆柱的表面积,圆柱表面积=底面积×2+侧面积。
22.12.56平方厘米 37.68立方厘米
【详解】思路分析:以AB为轴旋转一周后是一个底面半径为2高为2的圆柱和一个底面半径为2高为5-2=3的圆锥.根据公式来求底面积和体积.
名师解析:底面积=3.14×2×2=12.56(平方厘米)
体积=×12.56×(5-2)+12.56×2
=12.56+12.56
=37.68(立方厘米)
易错提示:沿AB为轴旋转后是什么图形不能正确把握,圆柱圆锥的体积公式掌握不牢固.
23.100.48 cm3
【分析】以这个直角三角形的6cm的直角边为轴旋转可形成底面半径为4cm,高为6cm的圆锥,根据圆锥的体积计算公式“V=πr2h”即可求出它的体积。
【详解】3.14×42×6×
=3.14×16×2
=100.48(cm3)
此题主要是考查圆锥的体积计算,关键是明白所形成的圆锥的底面半径及高,以直角三角形的一直角边为轴旋转一周形成的圆锥的高是为轴旋转的直角边,另一直角边为底面半径。
24.200.96立方分米
【分析】圆锥体积=底面积×高×,据此解答。
【详解】3.14×(8÷2)²×12×
=3.14×16×4
=200.96(立方分米)
圆锥的体积公式是解答此题的关键,注意计算时,要细心,不要出错。
25.376.8;1657.92
【分析】先根据“圆面积”求出圆柱的底面积,根据“圆周长”求出底面周长,再用“底面周长×高”求出侧面积,最后用“侧面积+底面积×2”求出圆柱的表面积。
【详解】
=150.72+226.08
=376.8()
=1256+401.92
=1657.92()
26.178.98平方厘米
【分析】利用圆柱体表面积公式:即可解答。
【详解】2×3.14×3×6.5+2×3×3.14
=122.46+56.52
=178.98(平方厘米)
此题主要考查了学生对圆柱表面积公式的运用。
27.722.2平方厘米;1105.28平方厘米
【解析】略
28.164.85平方厘米
【分析】将数据代入圆柱的表面积公式:S=2πr2+πdh,计算即可。
【详解】2×3.14×(5÷2)2+3.14×5×8
=3.14×6.25×2+3.14×40
=3.14×(12.5+40)
=3.14×52.5
=164.85(平方厘米)
29.219.8平方分米
【分析】根据圆柱表面积=底面积×2+侧面积,列式计算即可。
【详解】10÷2=5(分米)
3.14×52×2+3.14×10×2
=157+62.8
=219.8(平方分米)
所以,这个圆柱的表面积是219.8平方分米。
30.11.304平方厘米;12.56平方厘米
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式解答。
【详解】(1)3.14×2×0.8+3.14×(2÷2)2×2
=6.28×0.8+3.14×12×2
=5.024+3.14×2
= 5.024+6.28
=11.304(平方厘米)
这个圆柱的表面积是11.304平方厘米。
(2)2×3.14×0.5×3.5+3.14×0.52×2
=6.28×0.5×3.5+3.14×0.25×2
=3.14×3.5+0.785×2
=10.99+1.57
=12.56(平方厘米)
这个圆柱的表面积是12.56平方厘米。
31.169.56平方厘米
【分析】根据圆柱表面积公式,列式计算即可。
【详解】3.14×(6÷2)2×2+3.14×6×6
=56.52+113.04
=169.56(平方厘米)
本题考查了圆柱表面积,圆柱表面积=底面积×2+侧面积。
32.226.08平方厘米
【分析】根据圆柱表面积公式:,代数即可解答。
【详解】2×3.14×4×5+2×3.14×4
=125.6+100.48
=226.08(平方厘米)
此题主要考查学生的圆柱表面积解题能力,需要牢记表面积公式:。
33.(1)18.84cm;6.28cm;(2)7.065
【分析】(1)已知圆柱的底面直径d和高h,先求出底面半径r,用公式:r=d÷2,求表面积,用公式:S=2πrh+2πr,求体积,用公式:V=πrh,据此列式解答;
(2)已知圆锥的底面直径d和高h,先求出底面半径r,用公式:r=d÷2,求圆锥的体积V,用公式:V=πrh,据此列式解答。
【详解】(1)2÷2=1(cm)
3.14×2×2+3.14×12×2
=6.28×2+3.14×2
=12.56+6.28
=18.84(cm)
3.14×12×2
=3.14×2
=6.28(cm)
(2)3÷2=1.5
×3.14×1.52×3
=×3.14×2.25×3
=3.14×2.25
=7.065
此题主要考查学生对圆柱的侧面积、表面积,圆柱的体积(容积),圆锥的体积(容积)的公式运用和解答能力。
34.188.4立方厘米
【分析】由图可知,图形的体积=底面直径是6厘米的圆柱的体积-底面直径是(6-1×2)厘米圆柱的体积,根据圆柱的体积V=πr2h,代入数据计算即可。
【详解】6-1×2
=6-2
=4(厘米)
3.14×(6÷2)2×12-3.14×(4÷2)2×12
=3.14×9×12-3.14×4×12
=339.12-150.72
=188.4(立方厘米)
35.0.56cm2;0.024cm3
131.88cm2;113.04cm3
【分析】(1)根据长方体的表面积S=2(ab+ac+bc)、长方体的体积V=abh,列式计算即可;
(2)圆柱的表面积=2πrh+2πr2,圆柱的体积=πr2h,据此代入数据即可解答。
【详解】表面积:
(0.2×0.6+0.2×0.6+0.2×0.2)×2
=0.28×2
=0.56(cm2)
体积:0.6×0.2×0.2=0.024(cm3)
表面积:
3.14×6×4+3.14×(6÷2)2×2
=75.36+56.52
=131.88(cm2)
体积:3.14×(6÷2)2×4=113.04(cm3)
此题考查了长方体、圆柱体的表面积、体积公式的计算应用,熟记公式即可解答。
36.502.4立方厘米;392.5立方厘米.
【详解】试题分析:根据圆柱的体积公式:v=sh,圆锥的体积公式:v=sh,把数据分别代入公式解答.
解:3.14×42×10
=3.14×16×10
=502.4(立方厘米);
答:这个圆柱的体积是502.4立方厘米.
3.14×52×15
=3.14×25×15
=392.5(立方厘米);
答:这个圆锥的体积是392.5立方厘米.
【点评】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式.
37.15.7cm2
【分析】圆锥的侧面展开图的周长由两条半径和一段弧长组成,圆锥的表面积由圆锥的底面积和侧面展开图的面积相加得到,根据圆锥的侧面展开图的周长求出扇形的半径,根据底面周长求圆锥的底面半径,再根据圆锥的表面积计算方法求出其表面积即可。
【详解】解:设扇形的半径是厘米。
2x+1.57x=14.28
底面周长:
=8×3.14÷4
=25.12÷4
=6.28(cm)
底面半径:
=2÷2
=1(cm)
表面积:3.14×12+3.14×42÷4
=3.14×1+3.14×16÷4
=3.14+12.56
=15.7(cm2)
38.15162平方厘米
【分析】通过观察图形可知,半圆模型的表面积是由两个半圆面积加一半的圆柱侧面积加长方形面积组成,代数进行解答即可。
【详解】6分米=60厘米
3.14×(60÷2)+3.14×60×80÷2+60×80
=2826+7536+4800
=15162(平方厘米)
此题主要考查学生对圆柱表面积的理解与灵活应用,需要牢记圆柱表面积公式:和长方形面积公式:长×宽。
39.125.6平方厘米;100.48立方厘米
【分析】利用圆柱体表面积公式:和体积公式:以此解题。
【详解】表面积:2×3.14×2×8+2×2×3.14
=100.48+25.12
=125.6(平方厘米)
体积:3.14×2×8
=12.56×8
=100.48(立方厘米)
此题主要考查了圆柱体的表面积以及体积公式的应用。
40.2616立方厘米
【分析】根据圆锥的体积公式:v= ,长方体的体积公式:v=abh,把数据分别代入公式求出它们的体积和即可.
【详解】×3×(12÷2)2×6+20×15×8
=216+2400
=2616(立方厘米),
答:它的体积是2616立方厘米.
41.(1)100.48立方厘米;(2)150.72立方厘米
【分析】根据圆锥的体积公式:,代数解答即可。
【详解】(1)3.14×4×6×
=50.24×6×
=100.48(立方厘米)
(2)3.14×6×4×
=113.04×4×
=150.72(立方厘米)
此题主要考查学生对圆锥体积公式的灵活应用与解题能力,需要牢记公式。
42.536.94立方厘米
【分析】此组合图形由一个圆柱与2个圆锥组成,且圆柱与圆锥等底.根据圆柱的体积计算公式“V=πr2h”求出圆柱的体积,再根据圆锥的体积计算公式“V=πr2h”求出圆锥的体积,再把它们相加即可求解。
【详解】×3.14×(6÷2)2×6+×3.14×(6÷2)2×6+3.14×(6÷2)2×15
=×3.14×9×6+×3.14×9×6+3.14×9×15
=3.14×18+3.14×18+3.14×135
=3.14×(18+18+135)
=3.14×171
=536.94(立方厘米)
图形的体积是536.94立方厘米。
43.37.68cm3
【详解】×3.14×32×4
=×3.14×9×4
=37.68cm3
44.112cm2;386.9cm2
【分析】(1)观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;
所以组合图形的表面积=长方体的表面积+正方体4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算求解。
(2)观察图形可知,组合图形的表面积=圆柱侧面积的一半+圆的面积+长方形的面积,根据圆柱的侧面积公式S侧=πdh,圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】(1)4×4×6+2×2×4
=96+16
=112(cm2)
图形的表面积是112cm2。
(2)3.14×10×12÷2+3.14×(10÷2)2+10×12
=31.4×12÷2+3.14×25+120
=188.4+78.5+120
=386.9(cm2)
图形的表面积是386.9cm2。
45.240立方厘米
【分析】根据长方体体积公式:长×宽×高,代入数据求出体积即可。
【详解】10×4×6
=40×6
=240(立方厘米)
此题主要考查学生对长方体体积公式的实际应用解题能力,牢记公式是解题的关键。
46.
【分析】由题意可知:三角形各边放大的倍数一定,则放大后的边的长度与原来边的长度成正比,据此即可列比例求解。
【详解】由题意得:
8∶3.2=x∶2
3.2x=8×2
3.2x=16
3.2x÷3.2=16÷3.2
x=16÷3.2
x=5
放大后的边的长度是5cm。
47.1413立方米;3.14立方厘米;15.7立方厘米
【分析】利用圆柱体积公式:和圆锥体积公式:即可解答。
【详解】(1)圆柱体积:3.14×(10÷2)×18
=3.14×25×18
=1413(立方米)
(2)圆锥体积:×3.14×1×3
=3.14×1
=3.14(立方厘米)
(3)底面半径:2÷2=1(厘米)
圆柱体积:3.14×(2÷2)×4
=3.14×4
=12.56(立方厘米)
圆锥体积:×3.14×1×3
=3.14×1
=3.14(立方厘米)
组合体体积:12.56+3.14=15.7(立方厘米)
此题考查了学生对圆柱和圆锥体积公式的综合应用。
48.1884cm3
【分析】圆锥的体积=πr2h,把数值代入公式即可求解。
【详解】×3.14×102×18
=×3.14×100×18
=1884(cm3)
49.197.82立方厘米;127.17立方厘米
【分析】圆柱的体积=底面积×高,圆锥的体积=×底面积×高,据此解答即可。
【详解】3.14×32×7=197.82(立方厘米)
×3.14×(28.26÷3.14÷2)²×6
=×3.14×4.5²×6
=127.17(立方厘米)
故答案为:197.82立方厘米;127.17立方厘米
本题重点考查了圆锥和圆柱的体积公式,注意在图形中准确找到数据,带入公式计算。
50.18.84立方分米;282.6立方厘米.
【详解】试题分析:(1)根据圆锥的体积公式V=sh进行计算即可得到答案;
(2)根据圆柱的体积公式V=sh进行计算即可得到答案.
解:圆锥的体积为:3.14×22×4.5×
=3.14×4×1.5
=18.84(立方分米);
答:圆锥的体积是18.84立方分米.
圆柱的体积为:3.14×32×10
=3.14×9×10
=282.6(立方厘米);
答:圆柱的体积是282.6立方厘米.
【点评】此题主要考查的是圆柱和圆锥体体积公式的应用.
51.5.2656平方米;0.314立方米
【分析】观察图形可知,半个圆柱木料的表面积包含一个圆柱底面积、半个圆柱侧面积以及一个长为5m,宽为4dm的长方形面积;半个圆柱木料的体积正好是圆柱体积的一半,据此解答即可。
【详解】4分米=0.4米
表面积:0.4×5+3.14×(0.4÷2)2+3.14×0.4×5÷2
=2+0.1256+3.14
=5.2656(平方米)
体积:3.14×(0.4÷2)2×5÷2
=3.14×0.04×5÷2
=0.618÷2
=0.314(立方米)
本题主要考查了圆柱体积和面积的实际应用问题。
52.150.72立方米.
【详解】试题分析:根据圆锥的体积公式:v=sh,圆柱的体积公式:v=sh,把数据分别代入公式求出它们的体积和即可.
解:如图:
3.14×(6÷2)2×4+3.14×(6÷2)2×4
=3.14×9×4+3.14×9×4
=37.68+113.04
=150.72(立方米),
答:它的体积是150.72立方米.
【点评】此题主要考查圆锥、圆柱的体积公式的灵活运用,关键是熟记公式.
53.120平方厘米;207.24平方厘米
【分析】(1)长方体的表面积S=(ab+ah+bh)×2,据此代入数据即可求解;
(2)圆柱的表面积=侧面积+底面积×2,侧面积=底面周长×高,据此代入数据即可求解。
【详解】(1)6×6×2+6×2×4
=72+48
=120(平方厘米)
(2)3.14×6×8+3.14×(6÷2)2×2
=150.72+56.52
=207.24(平方厘米)
此题主要考查长方体和圆柱的表面积的计算方法的灵活应用。
54.25.12平方厘米
【分析】把该图形旋转一周后得到一个底面半径是1厘米,高是3厘米的圆柱体,再可求出这个圆柱体的表面积,据此解答。
【详解】3.14×12×2+3.14×1×2×3
=3.14×2+3.14×2×3
=6.28+6.28×3
=6.28+18.84
=25.12(平方厘米)
如图所示的图形绕轴旋转一周后形成的物体的表面积时25.12平方厘米。
55.249平方厘米
【分析】根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数值即可解答。
【详解】(8×5+8×6.5+6.5×5)×2
=(40+52+32.5)×2
=124.5×2
=249(平方厘米)
此题主要考查学生利用长方体表面积公式解答问题的能力,牢记公式是解题的关键。
56.(1)29.4375立方厘米;(2)35.325立方厘米
【分析】(1)利用圆锥体积公式进行解答即可;
(2)利用圆锥体积公式:和圆柱体积公式:即可求出组合图形体积。
【详解】(1)3.14×(5÷2)×4.5×
=3.14×6.25×4.5×
=19.625×4.5×
=29.4375(立方厘米)
(2)3.14×(3÷2)×3×+3.14×(3÷2)×4
=3.14×2.25×3×+3.14×2.25×4
=7.065+28.26
=35.325(立方厘米)
此题主要考查了学生对圆锥和圆柱体积公式的应用,熟练运用公式是解题的关键。
57.244.92平方分米;56.52立方厘米.
【详解】试题分析:(1)本题利用圆柱的底面圆的周长先求出半径,在运用圆柱的表面积=2个圆的面积+一个侧面的面积,即可求出圆柱的表面积;
(2)根据圆锥的体积=πr2h,代入数据即可解答.
解:(1)18.84÷3.14÷2,
=6÷2
=3(分米)
表面积=2个圆的面积+一个侧面的面积,
3.14×32×2+18.84×10
=56.52+188.4
=244.92(平方分米).
答:圆柱的表面积是244.92平方分米.
(2)×3.14×(6÷2)2×6
=3.14×9×2
=56.52(立方厘米)
答:圆锥的体积是56.52立方厘米.
【点评】本题主要考查了圆柱的表面积公式的运用,圆柱的表面积等于2个底面的面积加上一个侧面的面积.
(期中典型真题)专题7作图题-江苏省苏州市2023-2024学年六年级下册数学期中高频易错核心考点(苏教版): 这是一份(期中典型真题)专题7作图题-江苏省苏州市2023-2024学年六年级下册数学期中高频易错核心考点(苏教版),共45页。试卷主要包含了按要求画图,把如图的图形按2等内容,欢迎下载使用。
(期中典型真题)专题7综合计算-江苏省苏州市2023-2024学年四年级下册数学期中高频易错核心考点(苏教版): 这是一份(期中典型真题)专题7综合计算-江苏省苏州市2023-2024学年四年级下册数学期中高频易错核心考点(苏教版),共34页。试卷主要包含了口算,直接写出得数,估算等内容,欢迎下载使用。
(期中典型真题)专题6+综合计算-江苏省苏州市2023-2024学年六年级下册数学期中高频易错核心考点(苏教版): 这是一份(期中典型真题)专题6+综合计算-江苏省苏州市2023-2024学年六年级下册数学期中高频易错核心考点(苏教版),共47页。试卷主要包含了求的值,解方程,解方程或解比例,解比例,求未知数,求未知数x等内容,欢迎下载使用。













