综合解析-京改版八年级数学上册期末综合复习试题 卷（Ⅱ）（详解版）

这是一份综合解析-京改版八年级数学上册期末综合复习试题 卷（Ⅱ）（详解版），共19页。试卷主要包含了如图，∠1，化简的结果是等内容，欢迎下载使用。

考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 35分）
一、单选题（5小题，每小题3分，共计15分）
1、 （ ）
A．B．4C．D．
2、实数2021的相反数是（ ）
A．2021B．C．D．
3、给出下列命题，正确的有（ ）个①等腰三角形的角平分线、中线和高重合； ②等腰三角形两腰上的高相等； ③等腰三角形最小边是底边；④等边三角形的高、中线、角平分线都相等；⑤等腰三角形都是锐角三角形
A．1个B．2个C．3个D．4个
4、如图，∠1、∠2、∠3中是△ABC外角的是（ ）
A．∠1、∠2B．∠2、∠3C．∠1、∠3D．∠1、∠2、∠3
5、化简的结果是（ ）
A．B．C．D．
二、多选题（5小题，每小题4分，共计20分）
1、以下各式不是最简二次根式的是（ ）
A．B．C．D．
2、下列说法不正确的是（ ）
A．无理数就是开方开不尽的数B．无理数是无限不循环小数
C．带根号的数都是无理数D．无限小数都是无理数
3、如图，在△ABC中，AB=AC，∠BAD=∠CAD，则下列结论，正确的有（ ）
A．△ABD≌△ACDB．∠B=∠CC．BD=CDD．AD⊥BC．
4、下列计算正确的是（ ）
A．B．
C．D．
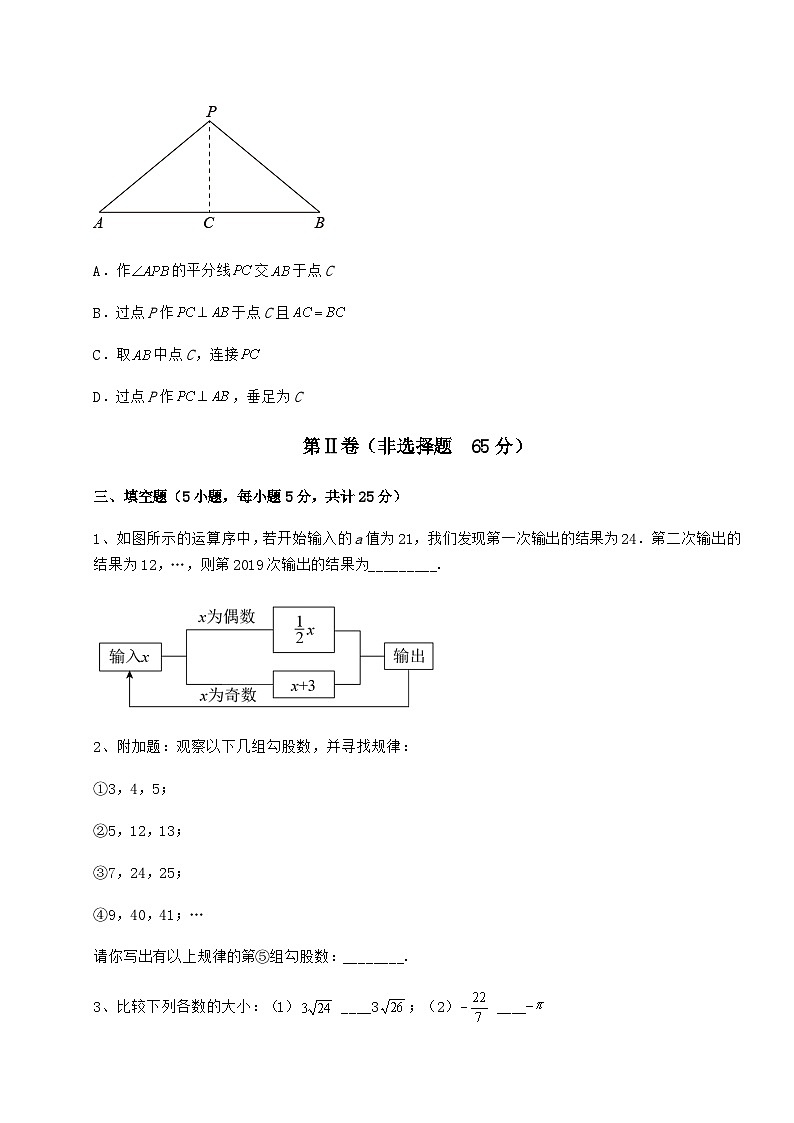
5、知：如图，点P在线段外，且，求证：点P在线段的垂直平分线上．在证明该结论时，需添加辅助线，则作法正确的是（ ）
A．作的平分线交于点C
B．过点P作于点C且
C．取中点C，连接
D．过点P作，垂足为C
第Ⅱ卷（非选择题 65分）
三、填空题（5小题，每小题5分，共计25分）
1、如图所示的运算序中，若开始输入的a值为21，我们发现第一次输出的结果为24．第二次输出的结果为12，…，则第2019次输出的结果为_________．
2、附加题：观察以下几组勾股数，并寻找规律：
①3，4，5；
②5，12，13；
③7，24，25；
④9，40，41；…
请你写出有以上规律的第⑤组勾股数：________．
3、比较下列各数的大小：（1） ____3；（2） ____-
4、在继承和发扬红色学校光荣传统，与时俱进，把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上，如图所示，一根旗杆的升旗的绳垂直落地后还剩余1米，若将绳子拉直，则绳端离旗杆底端的距离有5米．则旗杆的高度______．
5、计算：______．
四、解答题（5小题，每小题8分，共计40分）
1、2020年春季“新冠肺炎”在武汉全面爆发，蔓延全国，危及到人民生命安全，为了积极响应国家防控政策，双流区某镇政府采用了移动宣讲的形式进行宣传防控措施，如图，笔直公路的一侧点处有一村庄，村庄到公路的距离为600米，假设宣讲车周围1000米以内能听到广播宣传，宣讲车在公路上沿方向行驶时：
（1）请问村庄能否听到宣传，请说明理由；
（2）如果能听到，已知宣讲车的速度是200米/分钟，那么村庄总共能听到多长时间的宣传？
2、解分式方程：．
3、根据已学知识，我们已经能比较有理数的大小，下面介绍一种新的比较大小的方法：
①∵3－2＝1＞0，∴3＞2；②∵（－2）－1＝－3＜0，∴－2＜1；③∵（－2）－（－2）＝0，∴－2＝－2
像上面这样，根据两数之差是正数、负数或0，判断两数大小关系的方法叫做作差法比较大小．
(1)请将上述比较大小的方法用字母表示出来：
若，则_________；若，则_________；若，则_________；
(2)请用上述方法比较下列代数式的大小（直接在空格中填写答案）﹒
①______________；
②当时，____________；
(3)试比较与的大小，并说明理由．
4、计算：
（1）．
（2）．
5、如图，在△ABC中，∠ACB＝90°，用直尺和圆规在斜边AB上作一点P，使得点P到点B的距离与点P到边AC的距离相等．（保留作图痕迹，不写作法）
-参考答案-
一、单选题
1、B
【解析】
【分析】
直接利用二次根式的乘法运算法则计算得出答案．
【详解】
解：．
故选B．
【考点】
此题主要考查了二次根式的乘法运算，正确掌握运算法则是解题关键．
2、B
【解析】
【分析】
直接利用相反数的定义：只有符号不同的两个数互为相反数，即可得出答案．
【详解】
解：2021的相反数是：．
故选：B．
【考点】
本题主要考查相反数的定义，正确掌握其概念是解题关键．
3、B
【解析】
【详解】
解：①等腰三角形的顶角角平分线、底边上的中线和底边上的高重合，故本选项错误；
②等腰三角形两腰上的高相等，本选项正确；
③等腰三角形最小边不一定底边，故本选项错误；
④等边三角形的高、中线、角平分线都相等，本选项正确；
⑤等腰三角形可以是钝角三角形，故本选项错误，
故选B
4、C
【解析】
【分析】
根据三角形外角的定义进行分析即可得到答案.
【详解】
解：属于△ABC外角的有∠1、∠3共2个．故选C．
【考点】
本题考查三角形外角的定义，解题的关键是掌握三角形的定义.
5、D
【解析】
【分析】
最简公分母为，通分后求和即可．
【详解】
解：的最简公分母为，
通分得
故选D．
【考点】
本题考查了分式加法运算．解题的关键与难点是找出通分时分式的最简公分母．
二、多选题
1、ABC
【解析】
【分析】
根据最简二次根式的定义逐个判断即可．
【详解】
解：A、，不是最简二次根式，故本选项符合题意；
B、，不是最简二次根式，故本选项符合题意；
C、，不是最简二次根式，故本选项符合题意；
D、，是最简二次根式，故本选项不符合题意；
故选ABC．
【考点】
本题主要考查了最简二次根式的定义，最简二次根式的条件：（1）被开方数的因数是整数或整式；（2）被开方数中不含有可化为平方数或平方式的因数或因式．
2、ACD
【解析】
【分析】
根据无理数的定义以及性质，对选项逐个判断即可．
【详解】
解：A、无理数包含开方开不尽的数，选项说法错误，符合题意；
B、无限不循环小数统称无理数，选项正确，不符合题意；
C、带根号的数都是无理数，说法错误，比如，为有理数，符合题意；
D、无限不循环小数是无理数，无限循环小数是有理数，选项错误，符合题意；
故选ACD
【考点】
此题考查了无理数的定义以及性质，无限不循环小数是无理数，熟练掌握无理数的有关性质是解题的关键．
3、ABCD
【解析】
【分析】
由于，利用等边对等角，等腰三角形三线合一定理，可知，，，从而．
【详解】
∵在中，，
，
∴，，，
∴．
故选ABCD．
【考点】
本题考查了等腰三角形的性质、三角形全等的判定，等腰三角形的角平分线，底边上的中线，底边的高相互重合．
4、CD
【解析】
【分析】
利用幂的运算法则可判断 利用平方差公式的特点可判断 利用同底数幂的除法判断 利用合并同类项可判断 从而可得答案.
【详解】
解：，故不符合题意；
故不符合题意；
故符合题意；
故符合题意；
故选：
【考点】
本题考查的是幂的运算，负整数指数幂的含义，平方差公式的应用，合并同类项，掌握以上运算的运算法则是解题的关键.
5、ACD
【解析】
【分析】
利用全等三角形的判定对各个选项逐个判断即可得出结论．
【详解】
解：A、利用判断出，，，点在线段的垂直平分线上，符合题意；
B、过线段外一点作已知线段的垂线，不能保证也平分此条线段，不符合题意；
C、利用判断出，，，点在线段的垂直平分线上，符合题意；
D、利用判断出，，点在线段的垂直平分线上，符合题意；
故选：ACD．
【考点】
此题主要考查了全等三角形的判定，线段垂直平分线的判定，熟练掌握全等三角形的判定方法是解本题的关键．
三、填空题
1、6
【解析】
【分析】
根据程序图进行计算发现数字的变化规律，从而分析求解．
【详解】
解：当输入a=21时，
第一次输出的结果为，
第二次输出结果为，
第三次输出结果为，
第四次输出结果为，
第五次输出结果为，
第六次输出结果为，
…
自第三次开始，奇数次的输出结果为6，偶数次的输出结果为3，
∴第2019次输出的结果是6．
故答案为：6．
【考点】
本题考查代数式求值，准确识图，理解程序图，通过计算发现数字变化规律是解题关键．
2、11，60，61
【解析】
【分析】
由所给勾股数发现第一个数是奇数，且逐步递增2，知第5组第一个数是11，第二、第三个数相差为1，设第二个数为x，则第三个数为，由勾股定理得：，计算求解即可．
【详解】
解：由所给勾股数发现第一个数是奇数，且逐步递增2，
∴知第5组第一个数是11，
第二、第三个数相差为1，
设第二个数为x，则第三个数为，
由勾股定理得：，
解得x＝60，
∴第5组数是：11、60、61
故答案为：11、60、61．
【考点】
本题考查了数字类规律，勾股定理等知识．解题的关键在于推导规律．
3、 ＜； ＜
【解析】
【分析】
（1）根据数轴上表示的两个实数，右边的总比左边的大进行比较；（2）根据两个负数，绝对值大的反而小进行比较．
【详解】
解：（1）∵ ＜，
∴3＜；
（2） ≈-3.143，-π≈-3.141，
∵3.143＞3.141
∴ ＜-π．
故答案为＜，＜．
【考点】
本题考查了实数的大小比较，解题的关键是注意：正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小．
4、12米
【解析】
【分析】
设旗杆的高度是x米，绳子长为（x+1）米，旗杆，拉直的绳子和BC构成直角三角形，根据勾股定理可求出x的值，从而求出旗杆的高度．
【详解】
解：设旗杆的高度为米，根据题意可得：
，
解得：，
答：旗杆的高度为12米．
故答案为：12米．
【考点】
本题考查勾股定理的应用，关键看到旗杆，拉直的绳子和BC构成直角三角形，根据勾股定理可求解．
5、
【解析】
【分析】
根据实数的性质即可化简求解．
【详解】
解：
故答案为：．
【考点】
本题主要考查了实数的运算，解题的关键是掌握负指数幂的运算．
四、解答题
1、（1）村庄能听到宣传，理由见解析；（2）村庄总共能听到8分钟的宣传．
【解析】
【分析】
（1）直接比较村庄到公路的距离和广播宣传距离即可；
（2）过点作于点，利用勾股定理运算出广播影响村庄的路程，再除以速度即可得到时间．
【详解】
解：（1）村庄能听到宣传，
理由：∵村庄到公路的距离为600米1000米，
∴村庄能听到宣传；
（2）如图：过点作于点，
假设当宣讲车行驶到点开始影响村庄，行驶点结束对村庄的影响，
则米，米，
∴（米），
∴米，
∴影响村庄的时间为：（分钟），
∴村庄总共能听到8分钟的宣传．
【考点】
本题主要考查了垂线的性质，勾股定理，仔细审题获取相关信息合理作出图形是解题的关键．
2、
【解析】
【分析】
分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
【详解】
方程，
，
，
，
经检验是分式方程的解，
∴原分式方程的解为．
【考点】
本题考查了解分式方程．利用了转化的思想，解分式方程要注意检验．
3、 (1)＞，=，＜
(2)＜，＞
(3)，理由见详解
【解析】
【分析】
（1）根据作差法可作答；
（2）利用作差法即可作答；
（3）结合整式的加减混合运算法则，利用作差法即可作答；
(1)
∵，
∴；
∵，
∴；
∵，
∴，
故答案为：＞、=、＜；
(2)
①∵，
∴；
②∵，
又∵，
∴，
∴，
故答案为：＜、＞；
(3)
，
理由如下：
∵，
又∵，
∴，
∴．
【考点】
本题考查了实数比较大小、二次根式的加减混合运算、整式的加减混合运算等知识，掌握相关的加减混合运算法则是解答本题的关键．
4、（1）27；（2）
【解析】
【分析】
（1）首先计算乘方、除法和负指数幂，然后进行加减计算即可；
（2）按照幂的运算法则计算，再合并同类项．
【详解】
解：（1）
=
=
=27；
（2）
=
=
=
【考点】
本题主要考查了有理数的混合运算，整式的混合运算，熟练掌握实数以内的各种运算法则，是解题的关键．
5、详见解析
【解析】
【分析】
先作∠ABC的角平分线BD，再过点D作AC的垂线交AB于P，则利用PD∥BC得到∠PDB＝∠CBD，于是可证明∠PDB＝∠CBD，所以PB＝PD．
【详解】
解：如图，点P为所作．
【考点】
此题主要考查尺规作图，解题的关键是熟知角平分线的作法与平行线的性质.