2023年初中数学中考专项分类强化训练（含答案）：06 一次函数（通用版）

这是一份2023年初中数学中考专项分类强化训练（含答案）：06 一次函数（通用版），共19页。试卷主要包含了中国象棋是中华名族，之间对应关系的大致图象是等内容，欢迎下载使用。
考点1 平面直角坐标系及点的坐标特征
1.（•株洲）在平面直角坐标系中，点A（2，3）位于哪个象限？ （ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
2.（•甘肃）已知点P（m+2，2m4）在x轴上，则点P的坐标是 （ ）
A．（4，0） B．（0，4）
C．（4，0） D．（0，4）
3.（•济宁）已知点P（x，y）位于第四象限，并且xy+4（x，y为整数），写出一个符合上述条件的点P的坐标_______．
4.（•白银）中国象棋是中华名族
的文化瑰宝，因趣味性强，深受大众喜爱．如
图，若在象棋棋盘上建立平面直角坐标系，
使“帅”位于点（0，2），“马”位于点（4，
2），则“兵”位于点_________．
考点2 函数的基础知识
1.（•淄博）从某容器口以均匀地速度注入酒精，若液面高度h随时间t的变化情况如图所示，则对应容器的形状为（ ）

A． B．
C． D．
2.（•广元）函数的自变量x的取值范围是 （ ）
A．x1 B．x1 C．x1 D．x1

3.（•岳阳）函数中，自变量x的取值范围是（ ）
A．x≠0 B．x2
C．x0 D．x2且x≠0
4.（•无锡）函数中的自变量x的取值范围是 （ ）
A．x≠ B．x1
C．x D．x
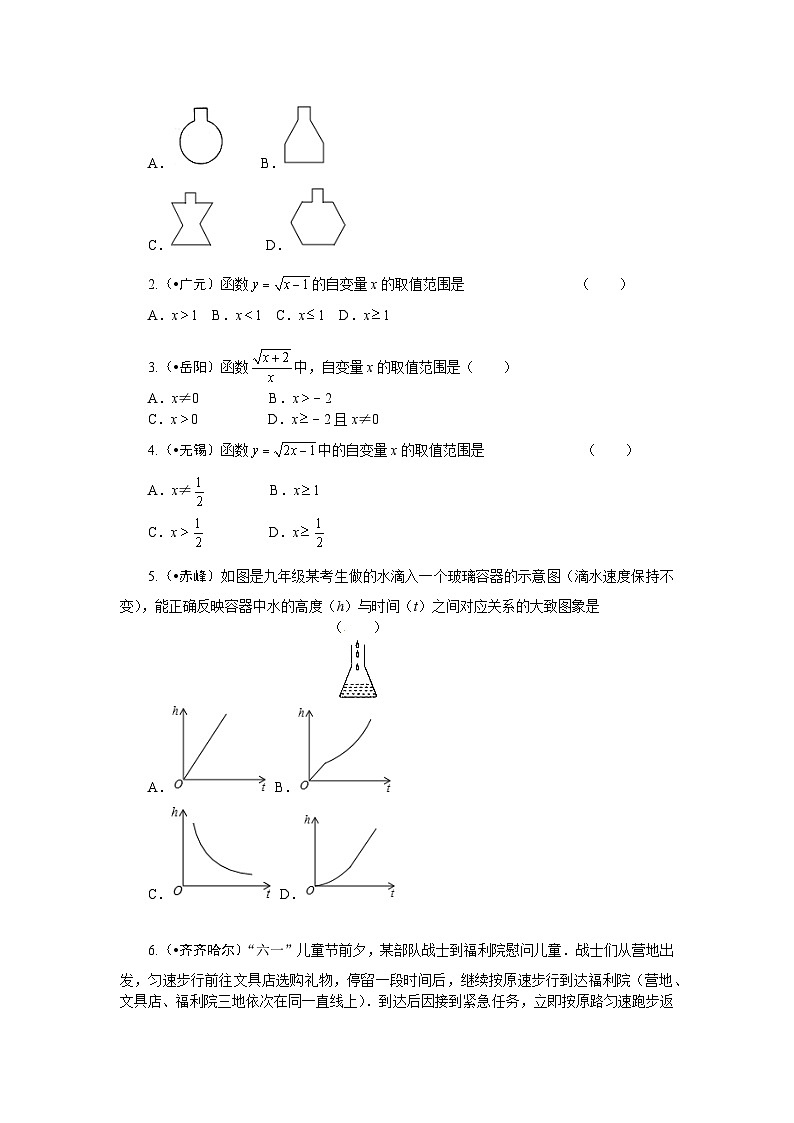
5.（•赤峰）如图是九年级某考生做的水滴入一个玻璃容器的示意图（滴水速度保持不变），能正确反映容器中水的高度（h）与时间（t）之间对应关系的大致图象是
（ ）

A． B．
C． D．
6.（•齐齐哈尔）“六一”儿童节前夕，某部队战士到福利院慰问儿童．战士们从营地出发，匀速步行前往文具店选购礼物，停留一段时间后，继续按原速步行到达福利院（营地、文具店、福利院三地依次在同一直线上）．到达后因接到紧急任务，立即按原路匀速跑步返回营地（赠送礼物的时间忽略不计），下列图象能大致反映战士们离营地的距离S与时间t之间函数关系的（ ）
A．B．
C．D．
7.（•孝感）一个装有进水管和出水管的空容器，从某时刻开始4min内只进水不出水，容器内存水8L；在随后的8min内既进水又出水，容器内存水12L；接着关闭进水管直到容器内的水放完．若每分钟进水量和出水量是两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的函数关系的图象大致的是 （ ）
A． B．
C． D．
8.（•随州）第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢．结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是 （ ）
A． B．
C． D．
9.（•黄冈）已知林茂的家、体育场、文具店在同一直线上，图中的信息反映的过程是：林茂从家跑步去体育场，在体育场锻炼了一阵后又走到文具店买笔，然后再走回家．图中x表示时间，y表示林茂离家的距离．依据图中的信息，下列说法错误的是
（ ）

A．体育场离林茂家2.5km
B．体育场离文具店1km
C．林茂从体育场出发到文具店的平均速度是50m/min
D．林茂从文具店回家的平均速度是60m/min
10.（•武汉）“漏壶”是一种古代计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度．人们根据壶中水面的位置计算时间，用t表示漏水时间，y表示壶底到水面的高度，下列图象适合表示y与x的对应关系的是 （ ）

A． B．
C． D．
考点3 一次函数的图象与性质
1.（•杭州）已知一次函数和，函数y1和y2的图象可能是 （ ）
A．B．C． D．
2.（•辽阳）若ab0且ab，则函数的图象可能是 （ ）
A． B．
C． D．
3.（•河池）函数的图象不经过 （ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
4.（•临沂）下列关于一次函数（k0，b0）的说法，错误的是
（ ）
A．图象经过第一、二、四象限
B．y随x的增大而减小
C．图象与y轴交于点（0，b）
D．当时，y0
5.（•大庆）正比例函数（k≠0）的函数值y随着x增大而减小，则一次函数的图象大致是 （ ）
A． B．
C． D．
6.（•杭州）某函数满足当自变量x=1时，函数值y=0，当自变量x=0时，函数值y=1，写出一个满足条件的函数表达式__________________．
7.（•乐山）如图，已知过点B（1，0）的直线l1与直线l2：相交于点P（1，a）．
（1）求直线l1的解析式；
（2）求四边形PAOC的面积．

考点4 一次函数的实际应用
1.（•聊城）某快递公司每天上午9：0010：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为
（ ）

A．9：15 B．9：20
C．9：25 D．9：30
2.（•东营）甲、乙两队参加了“端午情，龙舟韵”赛龙舟比赛，两队在比赛时的路程s（米）与时间t（秒）之间的函数图象如图所示，请你根据图象判断，下列说法正确的是 （ ）

A．乙队率先到达终点
B．甲队比乙队多走了126米
C．在47.8秒时，两队所走路程相等
D．从出发到13.7秒的时间段内，乙队的速度慢
3.（•威海）甲、乙施工队分别从两端修一段长度为380米的公路．在施工过程中，乙队曾因技术改进而停工一天，之后加快了施工进度并与甲队共同按期完成了修路任务．下表是根据每天工程进度绘制而成的．
下列说法错误的是 （ ）
A．甲队每天修路20米
B．乙队第一天修路15米
C．乙队技术改进后每天修路35米
D．前七天甲，乙两队修路长度相等
4.（•鄂尔多斯）在“加油向未来”电视节目中，王清和李北进行无人驾驶汽车运送货物表演，王清操控的快车和李北操控的慢车分别从A，B两地同时出发，相向而行．快车到达B地后，停留3秒卸货，然后原路返回A地，慢车到达A地即停运休息，如图表示的是两车之间的距离y（米）与行驶时间x（秒）的函数图象，根据图象信息，计算a、b的值分别为 （ ）

A．39，26 B．39，26.4
C．38，26 D．38，26.4
5.（•台湾）小涵与阿嘉一起去咖啡店购买同款咖啡豆，咖啡豆每公克的价钱固定，购买时自备容器则结帐金额再减5元．若小涵购买咖啡豆250公克且自备容器，需支付295元；阿嘉购买咖啡豆x公克但没有自备容器，需支付y元，则y与x的关系式为下列何者？ （ ）
A． B．
C． D．
6.（•郴州）某商店今年6月初销售纯净水的数量如下表所示：
观察此表，利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为______瓶．
7.（•重庆）某公司快递员甲匀速骑车前往某小区送物件，出发几分钟后，快递员乙发现甲的手机落在公司，无法联系，于是乙匀速骑车去追赶甲．乙刚出发2分钟时，甲也发现自己手机落在公司，立刻按原路原速骑车回公司，2分钟后甲遇到乙，乙把手机给甲后立即原路原速返回公司，甲继续原路原速赶往某小区送物件，甲乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示（乙给甲手机的时间忽略不计）．则乙回到公司时，甲距公司的路程是________米．

8.（•济宁）小王骑车从甲地到乙地，小李骑车从乙地到甲地，小王的速度小于小李的速度，两人同时出发，沿同一条公路匀速前进．图中的折线表示两人之间的距离y（km）与小王的行驶时间x（h）之间的函数关系．
请你根据图象进行探究：
（1）小王和小李的速度分别是多少？
（2）求线段BC所表示的y与x之间的函数解析式，并写出自变量x的取值范围．

9.（•德州）下表中给出A，B，C三种手机通话的收费方式．
（1）设月通话时间为x小时，则方案A，B，C的收费金额y1，y2，y3都是x的函数，请分别求出这三个函数解析式．
（2）填空：
若选择方式A最省钱，则月通话时间x的取值范围为________________；
若选择方式B最省钱，则月通话时间x的取值范围为_________________；
若选择方式C最省钱，则月通话时间x的取值范围为__________________；
（3）小王、小张今年5月份通话费均为80元，但小王比小张通话时间长，求小王该月的通话时间．
10.（•陕西）根据记录，从地面向上11km以内，每升高1km，气温降低6℃；又知在距离地面11km以上高空，气温几乎不变．若地面气温为m（℃），设距地面的高度为x（km）处的气温为y（℃）
（1）写出距地面的高度在11km以内的y与x之间的函数表达式；
（2）上周日，小敏在乘飞机从上海飞回西安途中，某一时刻，她从机舱内屏幕显示的相关数据得知，飞机外气温为26℃时，飞机距离地面的高度为7km，求当时这架飞机下方地面的气温；小敏想，假如飞机当时在距离地面12km的高空，飞机外的气温是多少度呢？请求出假如当时飞机距离地面12km时，飞机外的气温．
综合考点
一、选择题
1.（•娄底）如图，直线和与x轴分别交于点A（2，0），点B（3，0），则解集为（ ）

A． B．
C．或 D．
2.（•通辽）如图，直线经过点（1，3），则不等式的解集为 （ ）

A． B．
C． D．
3.（•苏州）若一次函数的图象经过点A（0，1），B（1，1），则不等式的解为 （ ）
A． B．
C． D．
4.（•辽阳）一条公路旁依次有A，B，C三个村庄，甲乙两人骑自行车分别从A村、B村同时出发前往C村，甲乙之间的距离s（km）与骑行时间t（h）之间的函数关系如图所示，下列结论：
①A，B两村相距10km；
②出发1.25h后两人相遇；
③甲每小时比乙多骑行8km；
④相遇后，乙又骑行了15min或65min时两人相距2km．
其中正确的个数是 （ ）

A．1个 B．2个 C．3个 D．4个
二、填空题
5.（•烟台）如图，直线与直线相交于点P（m，3），则关于x的不等式的解为__________．

6.（•黔东南州）如图所示，一次函数的图象经过点A（4，1），则不等式的解集为_____________．

7.（•无锡）已知一次函数的图象如图所示，则关于x的不等式的解集为___________．

8.（•滨州）如图，直线
经过点A（3，1），当时，x的取值范围为___________．

9.（•贵阳）在平面直角坐标系内，一次函数与的图象如图所示，则关于x，y的方程组的解是____________．

三、解答题
10.（•南京）已知一次函数（k为常数，k0）和．
（1）当k=2时，若y1y2，求x的取值范围．
（2）当x1时，y1y2．结合图象，直接写出k的取值范围．
参考答案
基础考点
考点1 平面直角坐标系及点的坐标特征
1.D 【解析】四个象限的符号特点分别是：
第一象限（+，+）；第二象限（，+）；
第三象限（，）；第四象限（+，）．点
A坐标为（2，3），则它位于第四象
限，故选D．
2.A 【解析】∵点P（m+2，2m4）在x轴上，∴2m4=0，解得m=2，∴m+2=4，
则点P的坐标是（4，0），故选A．
3.（1，2）（答案不唯一）
【解析】∵点P（x，y）位于第四象限，并且xy+4（x，y为整数），∴x0，y0，∴当x=1时，1y+4，解得0y3，∴y可以为2，故写一个符合上述条件的点P的坐标可以为（1，2）（答案不唯一），故答案为（1，2）（答案不唯一）．
4.（1,1） 【解析】如图所示：可得原点
位置，则“兵”位于（1，1）．

故答案为（1，1）．
考点2 函数的基础知识
1.C 【解析】根据图象可知，容器大致为：
容器底部比较粗，然后逐渐变细，然后
又逐渐变粗，最后又变得细小，并且最
后非常细，推断可能是C容器．故选C．
2.D 【解析】根据题意得x10，解得x1，
故选D．
3.D 【解析】根据题意得，解得
x2且x≠0，故选D．
4.D 【解析】根据题意得2x10，解得
x，故选D．
5.D 【解析】由于容器的形状是下宽上窄，
所以水的深度上升是先慢后快．表现出
的函数图形为先缓，后陡．故选D．
6.B 【解析】由题意可得，战士们从营地出
发到文具店这段过程中，S随t的增加
而增大，A项错误；战士们在文具店选
购文具的过程中，S随着t的增加不变，
战士们从文具店去福利院的过程中，S
随着t的增加而增大，C项错误；战士
们从福利院跑回营地的过程中，S随着
t的增大而减小，且在单位时间内距离
的变化比战士们从营地出发到文具店
这段过程中快，B项正确，D项错误，
故选B．[来源:学&科&网]
7.A 【解析】∵从某时刻开始4min内只进
水不出水，容器内存水8L；∴此时容
器内的水量随时间的增加而增加，∵随
后的8min内既进水又出水，容器内存
水12L，∴此时水量继续增加，只是增
速放缓，∵接着关闭进水管直到容器内
的水放完，∴水量逐渐减少为0，综上，
A项符合，故选A．
8.B 【解析】由于乌龟比兔子早出发，而早
到终点，B项正确，故选B．
9.C 【解析】从图中可知：体育场离文具店
的距离是，所用
时间是(4530)=15分钟，∴体育场出
发到文具店的平均m/min，
故选C．
10.A 【解析】∵不考虑水量变化对压力的
影响，水从壶底小孔均匀漏出，t表
示漏水时间，y表示壶底到水面的高
度，∴y随t的增大而减小，符合一
次函数图象，故选A．
考点3 一次函数的图象与性质
1.A 【解析】由①可知：a0，b0．∴直
线②经过一、二、三象限，A项正确；
由①可知：a0，b0．∴直线②经过
一、二、三象限，B项错误；由①可知：
a0，b0．∴直线②经过一、二、四
象限，交点不对，C项错误；由①可知：
a0，b＜0，∴直线②经过二、三、四
象限，D项错误．故选A．
2.A 【解析】∵ab0，且ab，∴a0，b
0，∴函数的图象经过第一、
三、四象限．故选A．
3.B 【解析】一次函数，∵k=10，
∴函数图象经过第一三象限，
∵b=20，∴函数图象与y轴负半轴
相交，∴函数图象经过第一三四象限，
不经过第二象限．故选B．
4.D 【解析】∵（k0，b0），
∴图象经过第一、二、四象限，A项正
确；∵k0，∴y随x的增大而减小，
B项正确；x=0时，y=b，∴图象与y
轴的交点为（0，b），C项正确；令y=0
时，当时，y0；D项
不正确，故选D．[来源:学&科&网]
5.A 【解析】∵正比例函数（k≠0）
的函数值y随x的增大而减小，∴k0，
∵一次函数的一次项系数大
于0，常数项小于0，∴一次函数
的图象经过第一、三象限，且
与y轴的负半轴相交．故选A．
6. 【解析】设该函数的解析式为
，∵函数满足当自
变量x=1时，函数值y=0，当
自变量x=0时，函数值y=1，
∴，解得，
所以函数的解析式为
，故答案为
．
7.【参考答案】（1）∵点P（1，a）在直线l2：y=2x+4上，∴2×(1)+4=a，即a=2，
则P的坐标为（1，2），
设直线l1的解析式为（k≠0），
那么，解得．
∴l1的解析式为．
（2）∵直线l1与y轴相交于点C，
∴C的坐标为（0，1），
又∵直线l2与x轴相交于点A，
∴A点的坐标为（2，0），则AB=3，
而S四边形PAOC=S△PABS△BOC，
∴S四边形PAOC=×3×2×1×1＝．
考点4 一次函数的实际应用
1.B 【解析】设甲仓库的快件数量y（件）
与时间x（分）之间的函数关系式为
，根据题意得
，解得k1=6，∴
；设乙仓库的快件数量y
（件）与时间x（分）之间的函数关系
式为，根据题意得
，解得k2=4，∴
，联立，
解得，∴此刻的时间为9：20，故
选B．
2.C 【解析】A项、由函数图象可知，甲走
完全程需要82.3秒，乙走完全程需要
90.2秒，甲队率先到达终点，错误；B
项、由函数图象可知，甲、乙两队都走
了300米，路程相同，错误；C项、由
函数图象可知，在47.8秒时，两队所走
路程相等，均无174米，正确；D项、
由函数图象可知，从出发到13.7秒的时
间段内，甲队的速度慢，错误，故选C．
3.D 【解析】由题意可得，甲队每天修路：
160140=20（米），A项正确；乙队第
一天修路3520=15（米），B项正确；
乙队技术改进后每天修路
21516020=35（米），C项正确；前
7天，甲队修路20×7=140米，乙队修
路270140=130米，D项错误，故选
D．
4.B 【解析】速度和为
24÷(3018)=2米/秒，由题意得
，解得b=26.4，因此慢车
速度为米/秒，快车速度为
20.8=1.2米/秒，快车返回追至两车距
离为24米的时间：
(26.424)÷(1.20.8)=6秒，因此
a=33+6=39秒．故选B．
5.B 【解析】根据题意可得咖啡豆每公克的
价钱为(295+5)÷250=（元），∴y
与x的关系式为，故选B.
6.150 【解析】这是一个一次函数模型，设
，则有，解得
，∴，当x=7时，
y=150，∴预测今年6月7日该商店
销售纯净水的数量约为150瓶，故答
案为150．
7.6000 【解析】由题意可得，甲的速度为
4000÷（1222）=500米/分，乙
的速度为
米/分，
乙从与甲相遇到返回公司用的时间
为4分钟，则乙回到公司时，甲距公
司的路程是
（米）,故答案为6000．
8.【参考答案】（1）由图可得，
小王的速度为km/h，
小李的速度为km/h，
答：小王和小李的速度分别是10km/h、20km/h.
（2）小李从乙地到甲地用的时间为
h，
当小李到达甲地时，两人之间的距离为
km，
∴点C的坐标为（1.5，15），
设线段BC所表示的y与x之间的函数解析式为，则，
得，
即线段BC所表示的y与x之间的函数解析式是．
9.【参考答案】（1）∵0.1元/min=6元/h，
∴由题意可得，，
，；
（2）；；
【解析】作出函数图象如图：
结合图象可得：
若选择方式A最省钱，则月通话时间x的取值范围为，
若选择方式B最省钱，则月通话时间x的取值范围为，
若选择方式C最省钱，则月通话时间x的取值范围为.
故答案为，，．
（3）∵小王、小张今年5月份通话费均为80元，但小王比小张通话时间长，
∴结合图象可得：小张选择的是方式A，小王选择的是方式B，
将y=80分别代入，
可得，解得x=55，
∴小王该月的通话时间为55小时．
10.【参考答案】（1）根据题意得；
（2）将x=7，y=26代入，
得，∴m=16
∴当时地面气温为16℃
∵x=1211，∴y=166×11=50（℃）
答：假如当时飞机距地面12km时，飞机外的气温为50℃．
综合考点
一、选择题
1.D 【解析】∵直线和与
x轴分别交于点A（2，0），
点B（3，0），则解集为
，故选D.
2.D 【解析】观察图象知：当时，
，故选D．
3.D 【解析】如图所示：不等式的
解为．故选D．

4.D 【解析】由图象可知A村、B村相离
10km，故①正确；当1.25h时，甲、乙
相距为0km，故在此时相遇，故②正确；
当0t1.25时，易得一次函数的解析
式为，故甲的速度比乙的速
度快8km/h．故③正确；当1.25t2
时，函数图象经过点（1.25，0）（2，6）
设一次函数的解析式为，代入
得，解得，∴
.当s=2时．得，解
得t=1.5h∴同
理当2t2.5时，设函数解析式为
，将点（2，6）（2.5，0）代入
得，解得，∴
.当s=2时，得
，解得t=，
，故相遇后，乙
又骑行了15min或65min时两人相距
2km，④正确．故选D．
二、填空题
5. 【解析】点P（m，3）代入，
∴m=1，∴P（1，3），结合图象可知
的解为，故答案为
.
6. 【解析】函数的图象如图
所示，图象经过点A（4，1），且
函数值y随x的增大而增大，故不
等式的解集是．故
答案为．
7. 【解析】∵图象过（6，0），则
，则，故
，∵k0，∴
，解得x2，答案为x2．
8. 【解析】∵正比例函数也经
过点A，∴的解集为
，故答案为．
9. 【解析】∵一次函数与
的图象的交点坐标为
（2，1），∴关于x，y的方程组
的解是．故答案
为．
三、解答题
10.【参考答案】（1）k=2时，
根据题意得，解得；
（2）4k1且k0日期
1
2
3
4
数量（瓶）
120
125
130
135
收费方式
月通话费/元
包时通话时间/h
超时费/元/min
A
30
25
0.1
B
50
50
0.1
C
100
不限时
/