




高中数学人教A版 (2019)必修 第一册4.1 指数评课课件ppt
展开1.学会根式与分数指数幂之间的相互转化;2.理解实数指数幂的运算性质;3.能用实数指数幂运算性质化简、求值.
知识点一 实数指数幂的运算性质思考1 在实数指数幂ax中,为什么要规定a>0?答案 把指数扩大为全体实数后,若a<0,ax有时没有意义,如 为运算方便,规定a>0.一般地,在研究实数指数幂的运算性质时,约定底数为大于零的实数.
问题导学 新知探究 点点落实
思考2 初中,我们知道a≠0,m
一般地,当a>0,b>0时,有:(1)am·an=am+n;(2)(am)n=amn;(3)(ab)n=anbn.其中m,n∈R.
知识点二 实数指数幂的化简思考 如何化简 ?答案
一般地,实数指数幂的化简中,先把根式、公式都化为实数指数幂的形式,再利用指数幂运算性质化简.
题型探究 重点难点 个个击破
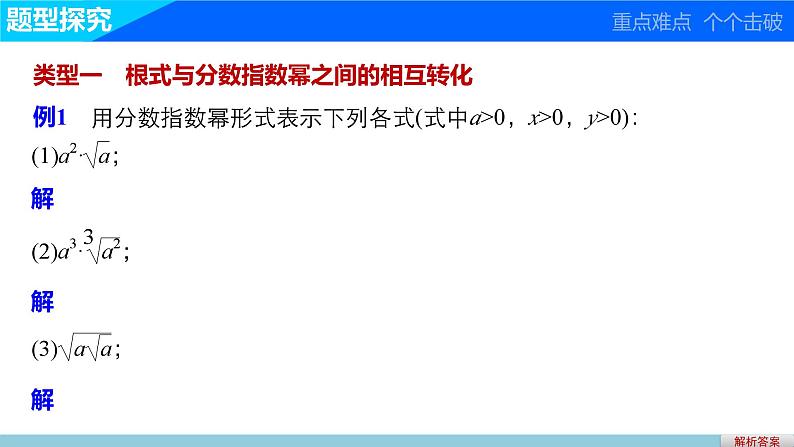
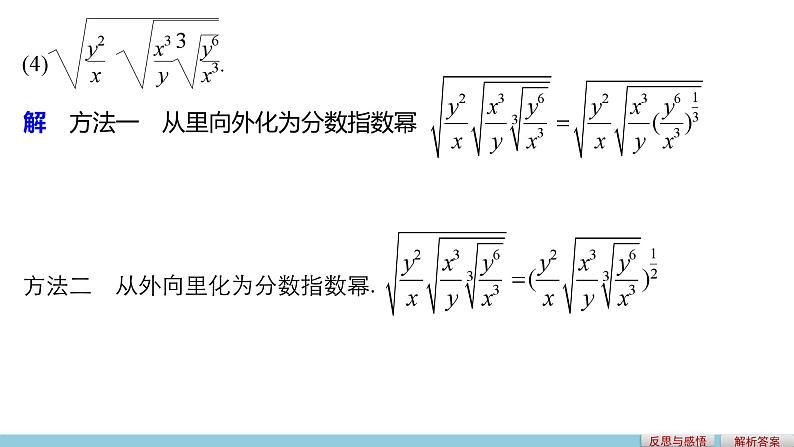
类型一 根式与分数指数幂之间的相互转化例1 用分数指数幂形式表示下列各式(式中a>0,x>0,y>0):
解 方法一 从里向外化为分数指数幂
方法二 从外向里化为分数指数幂.
(1)根式直观,分数指数幂易运算.(2)运算化简时要注意公式的前提条件,保持式子运算前后恒等.
跟踪训练1 把下列根式化成分数指数幂:
类型二 用指数幂运算公式化简求值例2 计算下列各式(式中字母都是正数):
一般地,进行指数幂运算时,可按系数、同类字母归在一起,分别计算;化负指数为正指数,化小数为分数进行运算,便于进行乘除、乘方、开方运算,可以达到化繁为简的目的.
跟踪训练2 (1)化简:
解 由 两边同时平方得x+2+x-1=25,
类型三 运用指数幂运算公式解方程例3 已知a>0,b>0,且ab=ba,b=9a,求a的值.解 方法一 ∵a>0,b>0,又ab=ba,
方法二 因为ab=ba,b=9a,所以a9a=(9a)a,即(a9)a=(9a)a,
指数取值范围由整数扩展到有理数乃至实数,给运算带来了方便,我们可以借助指数运算法则轻松对指数变形,以达到我们代入、消元等目的.
解 由67x=33,得 603y=81得
1.化简 的值为( )A.2 B.4 C.6 D.8
A. B. C. D.
5.计算 的结果是( )A.32 B.16 C.64 D.128
1.指数幂的一般运算步骤是:有括号先算括号里的;无括号先做指数运算.负指数幂化为正指数幂的倒数.底数是负数,先确定符号,底数是小数,先要化成分数,底数是带分数,先要化成假分数,然后要尽可能用幂的形式表示,便于用指数运算性质.2.根据一般先转化成分数指数幂,然后再利用有理数指数幂的运算性质进行运算.在将根式化为分数指数幂的过程中,一般采用由内到外逐层变换为指数的方法,然后运用运算性质准确求解.
高中数学北师大版必修12.1指数概念的扩充示范课课件ppt: 这是一份高中数学北师大版必修12.1指数概念的扩充示范课课件ppt,共31页。PPT课件主要包含了复习回顾,函数定义,是函数吗,3yx与,是同一函数吗等内容,欢迎下载使用。
高中数学北师大版必修12.1指数概念的扩充多媒体教学课件ppt: 这是一份高中数学北师大版必修12.1指数概念的扩充多媒体教学课件ppt,共17页。PPT课件主要包含了学习目标,基督与奸妇,引入,指数幂,新课探究,正整数指数幂,零指数幂,负整数指数幂,分数指数幂,概念形成等内容,欢迎下载使用。
北师大版必修12.1指数概念的扩充教课ppt课件: 这是一份北师大版必修12.1指数概念的扩充教课ppt课件,共25页。PPT课件主要包含了复习回顾,实例分析,请思考,函数的概念,是不是函数,函数定义,一对一,多对一,是函数吗,3yx与等内容,欢迎下载使用。













