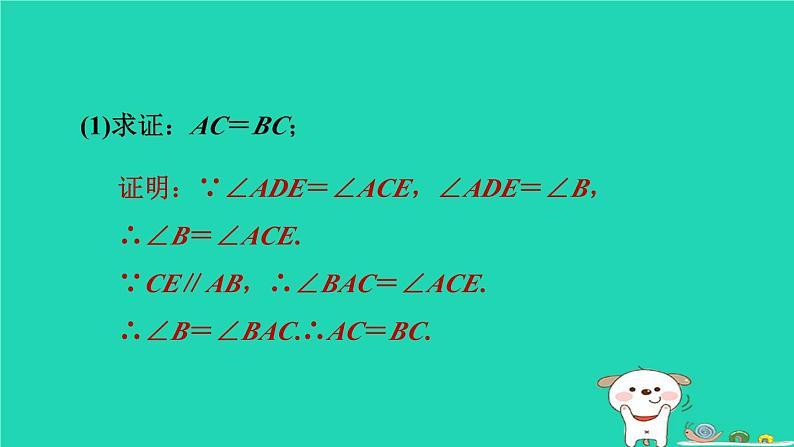
2024九年级数学下册提练第3招圆中常用的作辅助线的八种方法习题课件新版冀教版

这是一份2024九年级数学下册提练第3招圆中常用的作辅助线的八种方法习题课件新版冀教版，共37页。
第3招 圆中常用的作辅助线的八种方法冀教版 九年级下册1. 如图，两个正方形彼此相邻，且大正方形ABCD的顶点A，D在半圆O上，顶点B，C在半圆O的直径上；小正方形BEFG的顶点F在半圆O上，点E在半圆O的直径上，点G在大正方形的边AB上．若小正方形的边长为4 cm，求该半圆的半径．【点方法】在有关圆的计算题中，求角度或边长时，常连接半径构造等腰三角形或直角三角形，利用特殊三角形的性质来解决问题．2. [2023·成都]如图，以△ABC的边AC为直径作⊙O，交BC边于点D，过点C作CE∥AB交⊙O于点E，连接AD，DE，∠B＝∠ADE.(1)求证：AC＝BC；证明：∵∠ADE＝∠ACE，∠ADE＝∠B，∴∠B＝∠ACE.∵CE∥AB，∴∠BAC＝∠ACE.∴∠B＝∠BAC.∴AC＝BC.(2)若tan B＝2，CD＝3，求AB和DE的长．3. [2023·陕西] [新考法·相似比法]如图，△ABC内接于⊙O，∠BAC＝45°，过点B作BC的垂线，交⊙O于点D，并与CA的延长线交于点E，作BF⊥AC，垂足为M，交⊙O于点F.(1)求证：BD＝BC；证明：如图，连接DC，则∠BDC＝∠BAC＝45°.∵BD⊥BC，∴∠DBC＝90°，∴∠BCD＝90°－∠BDC＝ 45°，∴∠BCD＝∠BDC. ∴BD＝BC.(2)若⊙O的半径r＝3，BE＝6，求线段BF的长．4. [2023·福州第十八中学模拟]如图，四边形ABCD中，AB＝AD＝CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E，连接BC.(1)求证：OD∥BC；∵AD＝CD，∴DE⊥AC.∵AB为⊙O的直径，∴∠ACB＝90°，即BC⊥AC.∴OD∥BC.(2)若tan∠ABC＝2，求证：DA与⊙O相切．∴AO2＋AD2＝OD2，∴∠OAD＝90°，即OA⊥AD.∵OA是⊙O的半径，∴DA与⊙O相切．5.如图，△ABC为⊙O的内接三角形，AB＝AC，连接AO并延长交BC于点M.证明：∵△ABC为⊙O的内接三角形，∴点O在线段BC的垂直平分线上，∵AB＝AC，∴点A在线段BC的垂直平分线上，∴OA是线段BC的垂直平分线，∴AM⊥BC；(1)求证：AM⊥BC；6. 如图，在△ABC中，AB＝BC＝2，以AB为直径的⊙O分别交BC，AC于点D，E，且点D是BC的中点．证明：如图，连接AD，∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BD.∵点D是BC的中点，∴AD是线段BC的垂直平分线．∴AB＝AC. 又∵AB＝BC，∴AB＝BC＝AC.∴△ABC为等边三角形．(1)求证：△ABC为等边三角形．解：如图，连接BE.∵AB是⊙O的直径，∴∠AEB＝90°，即BE⊥AC.∵△ABC是等边三角形，∴AE＝EC，即E为AC的中点．(2)求DE的长．7.如图，⊙O是Rt△ABC的外接圆，∠ABC＝90°，点P是圆外一点，PA切⊙O于点A，且PA＝PB.证明：如图，连接OB，∵OA＝OB，∴∠OAB＝∠OBA.　∵PA＝PB，∴∠PAB＝∠PBA.∴∠OAB＋∠PAB＝∠OBA＋∠PBA，即∠PAO＝∠PBO.(1)求证：PB是⊙O的切线；∵PA是⊙O的切线，∴∠PAO＝90°.∴∠PBO＝90°，即OB⊥PB.又∵OB是⊙O的半径，∴PB是⊙O的切线．解：如图，连接OP，∵PA＝PB，∴点P在线段AB的垂直平分线上．∵OA＝OB，∴点O在线段AB的垂直平分线上．∴OP为线段AB的垂直平分线．∵∠ABC＝90°，∴BC⊥AB.∴PO∥BC.∴∠AOP＝∠ACB＝60°.由(1)知∠PAO＝90°.∴∠APO＝30°.∴PO＝2AO.∵在Rt△APO中，AO2＋PA2＝PO2，∴AO2＋3＝(2AO)2.∴AO2＝1.又∵AO＞0，∴AO＝1.即⊙O的半径为1.8. [2023·十堰模拟]如图，在△ABC中，AB＝AC，AD平分∠BAC，∠ACB的平分线交AD于点F，E为AC上一点，以CE为直径的⊙O经过点F，交BC于另一点G.证明：如图，连接OF，∵CF平分∠ACD，∴∠OCF＝∠FCD，∵OF＝OC，∴∠OFC＝∠OCF，∴∠FCD＝∠OFC，∴OF∥CD，∴∠AFO＝∠ADC，(1)求证：AD是⊙O的切线．∵AB＝AC，AD平分∠BAC，∴AD⊥BC，∴∠ADC＝90°，∴∠AFO＝∠ADC＝90°，∴OF⊥AD.又∵OF为⊙O的半径，∴AD是⊙O的切线；(2)若BC＝4，CF＝2DF，求阴影部分的面积．