专题25 几何压轴题（共51题）-学易金卷：5年（2019-2023）中考1年模拟数学真题分项汇编（北京专用）

这是一份专题25 几何压轴题（共51题）-学易金卷：5年（2019-2023）中考1年模拟数学真题分项汇编（北京专用），文件包含专题25几何压轴题共51题原卷版docx、专题25几何压轴题共51题解析版docx等2份试卷配套教学资源，其中试卷共140页， 欢迎下载使用。

1．（2023·北京·统考中考真题）在中、，于点M，D是线段上的动点（不与点M，C重合），将线段绕点D顺时针旋转得到线段．

(1)如图1，当点E在线段上时，求证：D是的中点；
(2)如图2，若在线段上存在点F（不与点B，M重合）满足，连接，，直接写出的大小，并证明．
2．（2022·北京·统考中考真题）在中，，D为内一点，连接，，延长到点，使得
(1)如图1，延长到点，使得，连接，，若，求证：；
(2)连接，交的延长线于点，连接，依题意补全图2，若，用等式表示线段与的数量关系，并证明．
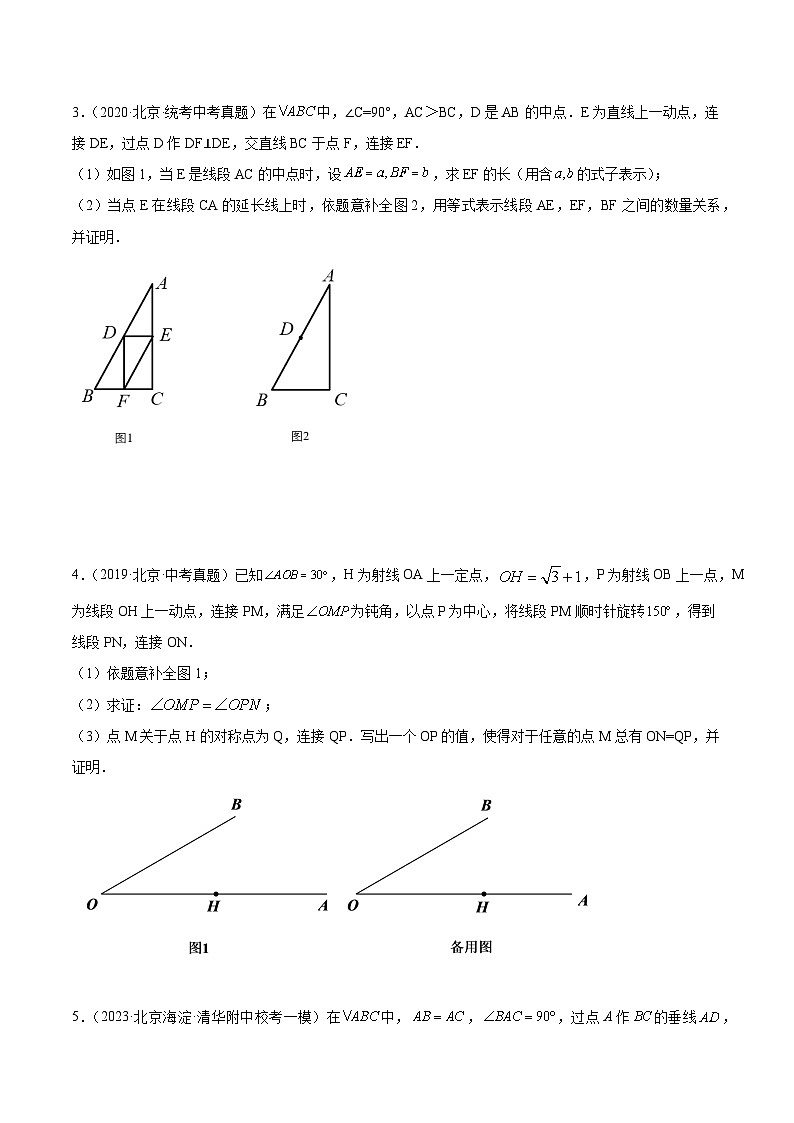
3．（2020·北京·统考中考真题）在中，∠C=90°，AC＞BC，D是AB的中点．E为直线上一动点，连接DE，过点D作DF⊥DE，交直线BC于点F，连接EF．
（1）如图1，当E是线段AC的中点时，设，求EF的长（用含的式子表示）；
（2）当点E在线段CA的延长线上时，依题意补全图2，用等式表示线段AE，EF，BF之间的数量关系，并证明．
4．（2019·北京·中考真题）已知，H为射线OA上一定点，，P为射线OB上一点，M为线段OH上一动点，连接PM，满足为钝角，以点P为中心，将线段PM顺时针旋转，得到线段PN，连接ON．
（1）依题意补全图1；
（2）求证：；
（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON=QP，并证明．
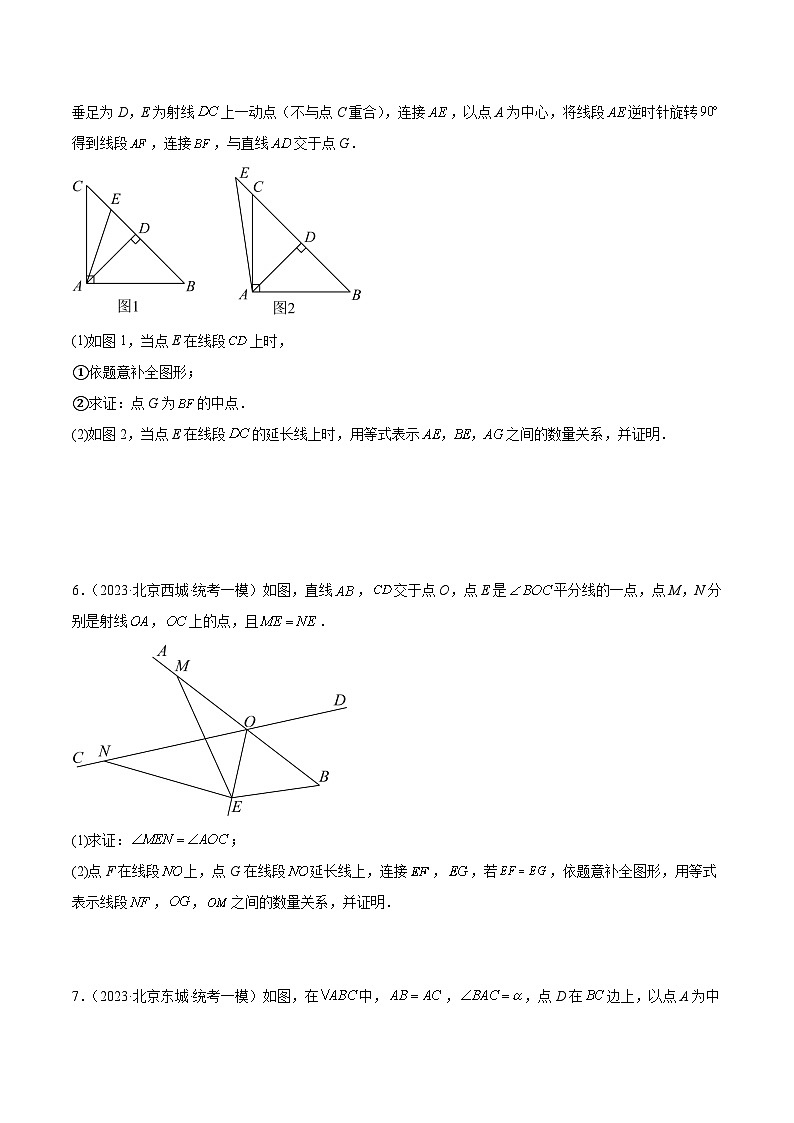
5．（2023·北京海淀·清华附中校考一模）在中，，，过点A作的垂线，垂足为D，E为射线上一动点（不与点C重合），连接，以点A为中心，将线段逆时针旋转得到线段，连接，与直线交于点G．
(1)如图1，当点E在线段上时，
①依题意补全图形；
②求证：点G为的中点．
(2)如图2，当点E在线段的延长线上时，用等式表示之间的数量关系，并证明．
6．（2023·北京西城·统考一模）如图，直线，交于点O，点E是平分线的一点，点M，N分别是射线，上的点，且．
(1)求证：；
(2)点F在线段上，点G在线段延长线上，连接，，若，依题意补全图形，用等式表示线段，，之间的数量关系，并证明．
7．（2023·北京东城·统考一模）如图，在中，，，点D在边上，以点A为中心，将线段顺时针旋转得到线段，连接．
(1)求证：平分；
(2)连接交于点F，过点C作，交的延长线于点G．补全图形，用等式表示线段与之间的数量关系，并证明．
8．（2023·北京朝阳·统考一模）如图，，点A在上，过点A作的平行线，与的平分线交于点B，点C在上（不与点O，B重合），连接，将线段绕点A顺时针旋转，得到线段，连接．
(1)直接写出线段与之间的数量关系，并证明；
(2)连接并延长，分别交，于点E，F．若，用等式表示线段与之间的数量关系，并证明．
9．（2023·北京海淀·统考二模）如图，在中，，，是的中点，是的中点，连接．将射线绕点逆时针旋转得到射线，过点作交射线于点．

(1)①依题意补全图形；
②求证：；
(2)连接，，用等式表示线段，之间的数量关系，并证明．
10．（2023·北京海淀·统考一模）如图，正方形中，点E，F分别在上，交于点G．
(1)求的度数；
(2)在线段上截取，连接的角平分线交于点N．
①依题意补全图形；
②用等式表示线段与的数量关系，并证明．
11．（2023·北京房山·统考二模）如图，，，点D是延长线上一点，连接，点E和点B关于直线对称，连接交于点F，连接．

(1)依题意补全图形，并求的度数；
(2)用等式表示线段和之间的数量关系，并证明．
12．（2023·北京西城·统考二模）如图，在中，边绕点B顺时针旋转（）得到线段，边绕点C逆时针旋转得到线段，连接，点F是的中点．

(1)以点F为对称中心，作点C关于点F的对称点G，连接．
①依题意补全图形，并证明；
②求证：；
(2)若，且于H，直接写出用等式表示的与的数量关系．
13．（2023·北京海淀·校考二模）已知等边，其中点D、E是过顶点B的一条直线l上两点
(1)如图1，，求证：
(2)如图2，，，，求AD的长．
14．（2023·北京丰台·统考一模）在正方形中，点O为对角线的中点，点E在对角线上，连接，点F在直线上（点F与点D不重合），且．
(1)如图1，当点E在线段上（不与端点重合）时．
①求证：；
②用等式表示线段，，的数量关系并证明；
(2)如图2，当点E在线段上（不与端点重合）时，补全图形，并直接写出线段，，的数量关系．
15．（2023·北京石景山·统考一模）在中，，，点为射线上一点，过点作且（点在点的右侧），射线交射线于点，点是的中点，连接，．
(1)如图，当点在线段上时，判断线段与的数量关系及位置关系；
(2)当点在线段的延长线上时，依题意补全图．用等式表示线段，，之间的数量关系，并证明．
16．（2023·北京东城·统考二模）如图，在菱形中，，E是边上一点（不与A，B重合），点F与点A关于直线对称，连接．作射线，交直线于点P，设．

(1)用含的代数式表示；
(2)连接．求证：是等边三角形；
(3)过点B作于点G，过点G作的平行线，交于点H．补全图形，猜想线段CH与PH之间的数量关系，并加以证明．
17．（2023·北京门头沟·统考一模）已知正方形和一动点E，连接，将线段绕点C顺时针旋转得到线段，连接，．
(1)如图1，当点E在正方形内部时，
①依题意补全图1；
②求证：；
(2)如图2，当点E在正方形外部时，连接，取中点M，连接，，用等式表示线段与的数量关系，并证明．
18．（2023·北京通州·统考一模）直线是线段的垂直平分线，垂足为点O，点C是直线上一点，连接．以为斜边作等腰直角，连接．
(1)如图1，若，求的度数；
(2)如图2所示，点E是直线上一点，且，连接，延长至点F，使得，连接．根据题意补全图2，写出线段之间的关系，并证明．
19．（2023·北京昌平·统考二模）在等边中，点是中点，点是线段上一点，连接，将射线绕点顺时针旋转，得到射线，点是射线上一点，且，连接.

(1)补全图形；
(2)求度数；
(3)用等式表示的数量关系，并证明.
20．（2023·北京平谷·统考一模）在中，，为边中点，连接，与相交于点，过作，交于点，连接．
(1)依题意补全图形；
(2)求证：；
(3)判断的数量关系，并证明．
21．（2023·北京朝阳·统考二模）在中，，，点D在边上（不与点B，C重合），将线段绕点A顺时针旋转，得到线段，连接．

(1)根据题意补全图形，并证明：；
(2)过点C作的平行线，交于点F，用等式表示线段与之间的数量关系，并证明．
22．（2023·北京·统考一模）如图，中，，，为边上一点（不与点，重合），连接，过点作于点，过点作，交直线于点．
(1)依题意补全图形；用等式表示线段与的数量关系，并证明；
(2)点为中点，连接，用等式表示线段，，之间的数量关系，并证明．
23．（2023·北京房山·统考一模）如图，正方形中，点是边上的一点，连接，将射线绕点逆时针旋转交的延长线于点，连接，取中点，连接．
(1)依题意补全图形；用等式表示与的数量关系，并证明；
(2)若，用等式表示线段与的数量关系，并证明．
24．（2023·北京朝阳·清华附中校考模拟预测）如图，中，，将线段绕点 A逆时针旋转得到点 D， 点 E 与点 D 关于直线对称，连接．
(1)依题意补全图形；
(2)判断的形状，并证明；
(3)请问在直线上是否存在点 P，使得 成立？若存在，请用文字描述出点 P 的准确位置，并画图证明；若不存在，请说明理由．
25．（2023·北京大兴·统考一模）在中，，，点为射线上一动点（不与点，重合），连接，点为延长线上一点，且，作点关于射线的对称点，连接，.
(1)如图1，当点在线段上时，
①依题意补全图形，求证：；
②用等式表示线段，，之间的数量关系，并证明；
(2)如图2，当点在线段的延长线上时，直接用等式表示线段，，之间的数量关系.
26．（2023·北京东城·北京市广渠门中学校考二模）如图，在中，，．是边上一点，交的延长线于点．
(1)用等式表示与的数量关系，并证明；
(2)连接，延长至，使．连接，，．
①依题意补全图形；
②判断的形状，并证明．
27．（2023·北京顺义·统考一模）已知：如图，中，，，点D在边上，点A关于直线的对称点为E，射线交直线于点F，连接．
(1)设，用含的代数式表示的大小，并求的度数；
(2)用等式表示线段，，之间的数量关系，并证明．
28．（2023·北京丰台·二模）如图，在等边中，点D，E分别在，的延长线上，且，的延长线交于点F．
(1)求的度数；
(2)延长至点G，使，连接交于点H．依题意补全图形，猜想线段与的数量关系，并证明．
29．（2023·北京海淀·校考一模）在中，，过点作射线，使（点与点在直线的异侧）点是射线上一动点（不与点重合），点在线段上，且．
(1)如图1，当点与点重合时，与的位置关系是________，若，则的长为________；（用含a的式子表示）
(2)如图2，当点与点不重合时，连接．
①用等式表示与之间的数量关系，并证明；
②用等式表示线段，，之间的数量关系，并证明．
30．（2023·北京延庆·统考一模）如图，在中，，，是边上的高，点E是边上的一动点（不与点A，B重合），连接交于点F，将线段绕点C顺时针旋转得到线段，连接．
(1)如图1，当是的角平分线时，
①求证：；
②直接写出_______°．
(2)依题意补全图2，用等式表示线段，，之间的数量关系，并证明．
31．（2023·北京门头沟·二模）如图，在中，，点在延长线上，且，将延方向平移，使点移动到点，点移动到点，点移动到点，得到，连接，过点作于．

(1)依题意补全图形；
(2)求证：；
(3)连接，用等式表示线段，的数量关系，并证明．
32．（2023·北京平谷·统考二模）在中，，点为边上一点，为延长线上的一点，，为边上一点，射线于点，过点作直线于，交于点，作的角平分线交于，过点作的平行线，交于点，交于点，交于点，．

(1)找出图中和相等的一个角，并证明；
(2)判断、、的数量关系，并证明．
33．（2023·北京石景山·统考二模）如图，在中，，，平分交于点，点是上一点且．
(1)求的大小（用含的式子表示）；
(2)连接，用等式表示线段与的数量关系，并证明．
34．（2023·北京顺义·统考二模）已知：，，分别是射线，上的点，连接，以点为旋转中心，将线段绕着点逆时针旋转，得到线段，连接，．
(1)如图1，当时，求证：；

(2)当时，依题意补全图2，用等式表示线段，，之间的数量关系，并证明．

35．（2023·北京大兴·统考二模）如图，在中，，将线段绕点A逆时针旋转得到线段，且点D落在的延长线上，过点D作于点E，延长交于点F．

(1)依题意补全图形．求证：；
(2)用等式表示线段与之间的数量关系，并证明．
36．（2023·北京西城·北京市第十三中学校考模拟预测）如图，在△ABC中，AB＝AC，∠BAC＝120°，D是BC中点，连接AD．点M在线段AD上（不与点A，D重合），连接MB，点E在CA的延长线上且ME＝MB，连接EB．
(1)比较∠ABM与∠AEM的大小，并证明；
(2)用等式表示线段AM，AB，AE之间的数量关系，并证明．
37．（2023·北京海淀·北理工附中校考模拟预测）如图，在四边形中，，，，作，使得点和点在直线异侧，连接，将射线绕点逆时针旋转90°交射线于点．
(1)①依题意，补全图形；
②证明：．
(2)连接，若为线段的中点，连接，请用等式表示线段与之间的数量关系，并证明．
38．（2023·北京海淀·首都师范大学附属中学校考一模）在等边中，点D为的中点，点E为上一点（不与A、D重合），连接．

将线段绕点E顺时针旋转至，使点F落在的延长线上，在图1中补全图形：
(1)求的度数；
(2)探究线段之间的数量关系，并加以证明；
(3)将线段绕点E旋转，在旋转过程中与边交于点H，连接，若，当时，请写出的最小值．
39．（2023·北京海淀·北京交通大学附属中学校考模拟预测）已知：在中，，，以为斜边作等腰，使得，两点在直线的同侧，过点作于点．
(1)如图1，当时，
①直接写出的度数；
②判断线段与的数量关系，并证明；
(2)当时，依题意补全图2，请直接写出线段与的数量关系（用含的式子表示）．
40．（2023·北京东城·北京市广渠门中学校考一模）如图，在中，，，点D在边上，将射线绕点B逆时针旋转得到射线，过点D作于E，延长到F，使，连接．
(1)依题意，补全图形，判断线段与的位置关系与数量关系，并证明；
(2)若H为线段的中点，连接，请用等式表示线段与之间的数量关系，并证明．
41．（2023·北京西城·北师大实验中学校考模拟预测）在中，，，过点作的垂线，垂足为，为射线上一动点（不与点重合），连接，以点为中心，将线段逆时针旋转得到线段，连接，与直线交于点．
(1)如图1，当点在线段上时，
①依题意补全图形；
②求证：点为的中点．
(2)如图2，当点在线段的延长线上时，用等式表示，，之间的数量关系，并证明．
42．（2023·北京东城·北京市广渠门中学校考模拟预测）如图，在中，，，点D在边上，将射线绕点逆时针旋转得到射线，过点作于，延长到，使，连接．
(1)依题意，补全图形，判断线段与的位置关系与数量关系，并证明；
(2)若为线段的中点，连接，请用等式表示线段与之间的数量关系，并证明．
43．（2023·北京·校考模拟预测）已知如图所示中，线段AC绕点A顺时针旋转，得到线段，过D作的垂线l，直线l上取一点E使得，连接．

(1)直接写出与大小关系 ；
(2)求与的面积比；
(3)延长使，连接，补全图形，并探究线段与线段的位置关系和数量关系，并证明．
44．（2023·北京·统考二模）中，，，点D为边的中点，点E在线段上，连接，将线段绕点A逆时针旋转得到线段，连接．
(1)如图1，当点E与点D重合时，求证：；
(2)当点E在线段上(与点C，D不重合)时，依题意补全图2；用等式表示线段，，之间的数量关系，并证明．
45．（2023·北京海淀·校考模拟预测）已知AB = BC，∠ABC = 90°，直线l是过点B的一条动直线（不与直线AB，BC重合），分别过点A，C作直线l的垂线，垂足为D，E．
(1)如图1，当45°＜∠ABD＜90°时，
①求证：CE +DE =AD；
②连接AE，过点D作DH⊥AE于H，过点A作AF∥BC交DH的延长线于点F．依题意补全图形，用等式表示线段DF，BE，DE的数量关系，并证明；
(2)在直线l运动的过程中，若DE的最大值为3，直接写出AB的长．
46．（2023·北京·校联考模拟预测）如图1，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC＝2，点M为BC中点．点P为AB边上一动点，点D为BC边上一动点，连接DP，以点P为旋转中心，将线段PD逆时针旋转90°，得到线段PE，连接EC．
（1）当点P与点A重合时，如图2．
①根据题意在图2中完成作图；
②判断EC与BC的位置关系并证明．
（2）连接EM，写出一个BP的值，使得对于任意的点D总有EM＝EC，并证明．
47．（2023·北京西城·北京市第十三中学分校校考模拟预测）如图，在等边中，点，分别在，的延长线上，且，的延长线交于点．

(1)求的度数；
(2)延长至点，使，连接交于点，依题意补全图形，猜想线段与的数量关系，并证明．
48．（2023·北京海淀·北京市十一学校校考模拟预测）如图，，，过点C作直线，点D，E是直线上的动点（D在E的右侧）且满足，连接，的平分线与射线交于点F，与射线交于点G．

(1)如图1，当点C在线段上，且时，若，求线段的长；
(2)如图2，当点D在点C左侧时，
①依题意补全图形；
②用等式表示线段，，的数量关系，并证明．
49．（2023·北京石景山·校考一模）如图，在中，，于点D，于点E，连接.
(1)依题意补全图形，猜想与之间的数量关系并证明；
(2)用等式表示线段，，的数量关系；并证明.
50．（2023·北京·校考模拟预测）如图，已知中，，D为斜边的中点，连接．过C点做的垂线，并在这条线上（C的下方）截取，连接．
(1)根据题目条件补全图形；
(2)证明：；
(3)用等式表示、和的数量关系，并证明．
51．（2023·北京海淀·北京市师达中学校考模拟预测）如图，在中，，，点是边上一个动点（不与，重合），连接，将线段绕点逆时针旋转，得到线段，连接．

(1)求的度数；
(2)过点作，交于点，交的延长线于点，连接，交于点；
①依据题意，补全图形；
②用等式表示线段，的数量关系，并证明．