专题15 矩形菱形正方形（共40题）-学易金卷：5年（2019-2023）中考1年模拟数学真题分项汇编（北京专用）

这是一份专题15 矩形菱形正方形（共40题）-学易金卷：5年（2019-2023）中考1年模拟数学真题分项汇编（北京专用），文件包含专题15矩形菱形正方形共40题原卷版docx、专题15矩形菱形正方形共40题解析版docx等2份试卷配套教学资源，其中试卷共74页， 欢迎下载使用。

1．（2023·北京·统考中考真题）如图，在中，点E，F分别在，上，，．

(1)求证：四边形是矩形；
(2)，，，求的长．
【答案】(1)见解析
(2)
【分析】（1）利用平行四边形的性质求出，证明四边形是平行四边形，然后根据对角线相等的平行四边形是矩形得出结论；
（2）证明是等腰直角三角形，可得，然后再解直角三角形求出即可．
【详解】（1）证明：∵四边形是平行四边形，
∴，，
∵，
∴，
∴四边形是平行四边形，
∵，
∴平行四边形是矩形；
（2）解：由（1）知四边形是矩形，
∴，
∵，，
∴是等腰直角三角形，
∴，
又∵，
∴，
∴，
∴．
【点睛】本题考查了平行四边形的判定和性质，矩形的判定和性质以及解直角三角形，熟练掌握相关判定定理和性质定理是解题的关键．
2．（2022·北京·统考中考真题）如图，在中，交于点，点在上，．

(1)求证：四边形是平行四边形；
(2)若求证：四边形是菱形．
【答案】见解析
【分析】（1）先根据四边形ABCD为平行四边形，得出，，再根据，得出，即可证明结论；
（2）先证明，得出，证明四边形ABCD为菱形，得出，即可证明结论．
【详解】（1）证明：∵四边形ABCD为平行四边形，
∴，，
∵，
∴，
即，
∴四边形是平行四边形．
（2）∵四边形ABCD为平行四边形，
∴，
∴，
∵
∴，
∴，
∴四边形ABCD为菱形，
∴，
即，
∵四边形是平行四边形，
∴四边形是菱形．
【点睛】本题主要考查了平行四边形的判定和性质，菱形的判定和性质，平行线的性质，熟练掌握菱形和平行四边形的判定方法，是解题的关键．
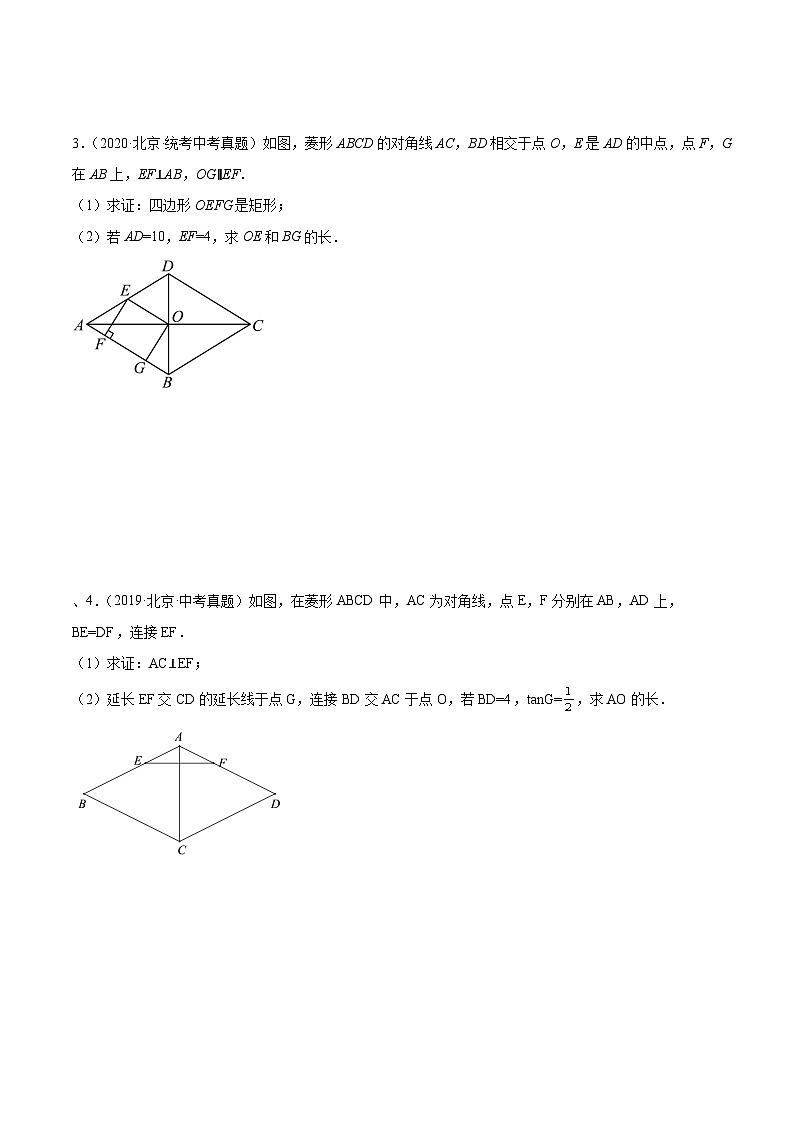
3．（2020·北京·统考中考真题）如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．
（1）求证：四边形OEFG是矩形；
（2）若AD=10，EF=4，求OE和BG的长．

【答案】(1)见解析；(2)OE=5，BG=2.
【分析】(1)先证明EO是△DAB的中位线，再结合已知条件OG∥EF，得到四边形OEFG是平行四边形，再由条件EF⊥AB，得到四边形OEFG是矩形；
(2)先求出AE=5，由勾股定理进而得到AF=3，再由中位线定理得到OE=AB=AD=5，得到FG=5，最后BG=AB-AF-FG=2．
【详解】解：(1)证明:∵四边形ABCD为菱形，
∴点O为BD的中点，
∵点E为AD中点，
∴OE为△ABD的中位线，
∴OE∥FG，
∵OG∥EF，∴四边形OEFG为平行四边形
∵EF⊥AB，∴平行四边形OEFG为矩形．
(2)∵点E为AD的中点，AD=10，
∴AE=
∵∠EFA=90°，EF=4，
∴在Rt△AEF中，．
∵四边形ABCD为菱形，
∴AB=AD=10，
∴OE=AB=5，
∵四边形OEFG为矩形，
∴FG=OE=5，
∴BG=AB-AF-FG=10-3-5=2．
故答案为：OE=5，BG=2．
【点睛】本题考查了矩形的性质和判定，菱形的性质、勾股定理等知识点，解题的关键是掌握特殊四边形的性质和判定属于中考常考题型，需要重点掌握．
4．（2019·北京·中考真题）如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE=DF，连接EF．
（1）求证：AC⊥EF；
（2）延长EF交CD的延长线于点G，连接BD交AC于点O，若BD=4，tanG=，求AO的长．
【答案】（1）证明见解析；（2）AO=1．
【分析】（1）由菱形的性质得出AB=AD，AC平分∠BAD，再根据等腰三角形的三线合一即可；
（2）根据菱形的性质和已知条件得出四边形EBDG为平行四边形，得出∠G=∠ABD，再根据tanG=即可求出AO的长．
【详解】（1）证明：∵四边形ABCD为菱形 ∴AB=AD，AC平分∠BAD
∵BE=DF， ∴ ， ∴AE=AF
∴△AEF是等腰三角形， ∵AC平分∠BAD， ∴AC⊥EF
（2）解：如图2所示：
∵四边形ABCD为菱形，∴CG∥AB，BO=BD=2，∵EF∥BD
∴四边形EBDG为平行四边形，∴∠G=∠ABD，∴tan∠ABD=tan∠G=
∴tan∠ABD=，∴AO=1
【点睛】本题考查了菱形的性质、平行线的判定与性质、解直角三角形，等腰三角形的性质等知识；熟练掌握菱形的性质是解题的关键．
5．（2023·北京西城·统考一模）在中，是边上的中线，点E在线段上，点F在线段的延长线上，，连接，．
(1)如图1，求证：四边形是平行四边形．
(2)若，
①依题意补全图2；
②求证：四边形为菱形.
【答案】见解析
【分析】（1）证明，可得，再根据，即可得出结论；
（2）由，可得，再由等腰三角形的性质可证，再利用菱形的判定即可得出结论．
【详解】（1）证明：∵ ，
∴ ，
∵ 是边上的中线，
∴ ，
∵，
∴，
∴ ，
∴四边形是平行四边形．
（2）解：①依题意补全图2，如图；
②证明：∵ ，
∴ ，
∵ 是边上的中线，
∴ ，
由（1）证明方法可得 四边形是平行四边形，
∴ 四边形为菱形．
【点睛】本题考查平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、平行线的性质及菱形的判定，熟练掌握平行四边形的判定与性质及菱形的判定是解题的关键．
6．（2023·北京东城·统考一模）如图，在平行四边形中，平分．
(1)求证：四边形是菱形；
(2)连接交于点O，延长到点E，在的内部作射线，使得，过点D作于点F．若，，求的度数及的长．
【答案】(1)见解析
(2)，
【分析】（1）由平行四边形的性质和角平分线的定义证明，得到，即可证明平行四边形是菱形；
（2）由菱形的性质可得，进而得到，；进一步求出，则由角平分线的性质得到，则．
【详解】（1）证明：∵四边形是平行四边形，
∴，
∴，
∵平分，
∴，
∴，
∴，
∴平行四边形是菱形；
（2）解：∵四边形是菱形，
∴，
∴，；
∵，
∴；
∵四边形是菱形，
∴，
∴，
又∵，
∴，
∴．
【点睛】本题主要考查了菱形的性质与判定，角平分线的性质和定义，平行四边形的性质，证明四边形是菱形是解题的关键．
7．（2023·北京朝阳·统考一模）如图，在平行四边形中，对角线相交于点O，点E，F在上，，连接．
(1)求证：四边形为平行四边形；
(2)若，求证：四边形是矩形．
【答案】见解析
【分析】（1）证明，得到，利用对角线互相平分的四边形是平行四边形，即可得证；
（2）证明，进而得到，即可得证．
【详解】（1）证明：∵四边形是平行四边形，
∴．
∵，
∴．
∵，
∴．
∴．
∴四边形为平行四边形．
（2）∵，
∴．
∵，
∴．
∴．
∴．
∴四边形是矩形．
【点睛】本题考查平行四边形的判定和性质，全等三角形的判定和性质，矩形的判定．熟练掌握相关知识点并灵活运用，是解题的关键．
8．（2023·北京海淀·统考二模）如图，平行四边形的对角线，交于点，为的中点．连接并延长至点，使得．连接，．

(1)求证：四边形为平行四边形；
(2)若，求证：四边形为矩形．
【答案】见解析
【分析】（1）证明为的中位线，则，且，又，则，即可得证；
（2）根据平行四边形的性质得出，则，根据已知的，可得，则四边形是菱形，可得，结合（1）的结论，即可得证．
【详解】（1）证明：∵平行四边形的对角线，交于点，
∴，
又，
∴为的中位线，
∴，且，
又为的中点，
∴，
∴，
∴四边形为平行四边形；
（2）∵平行四边形，
∴，
∴，
∵，
∴，
∴，
∴平行四边形是菱形，
∴，
∴，
∴平行四边形是矩形．
【点睛】本题考查了中位线的性质与判定，平行四边形的性质，菱形的性质与判定，矩形的判定，熟练掌握特殊四边形的判定定理是解题的关键．
9．（2023·北京海淀·统考一模）如图，在四边形中，，过点B作交于点E，点F为边上一点，，连接．
(1)求证：四边形为矩形；
(2)若，求的长．
【答案】(1)见解析
(2)10
【分析】（1）由题意易证四边形为平行四边形，再根据有一个角是直角的平行四边形是矩形即可判定；
（2）由题意易证，即得出，代入数据，即可求出的长，最后由勾股定理即可求解．
【详解】（1）证明：∵，即，，
∴四边形为平行四边形．
∵，
∴四边形为矩形；
（2）解：∵，
∴．
∵四边形为矩形，
∴，，
∴，
∴，即，
解得：，
∴．
【点睛】本题考查矩形的判定和性质，平行线的性质，相似三角形的判定和性质，勾股定理．熟练掌握上述知识是解题关键．
10．（2023·北京房山·统考二模）如图，点O为的对角线的中点，直线l绕点O旋转，当时，与边分别交于点E，F，连接．

(1)求证：四边形是菱形；
(2)若，求的面积．
【答案】(1)见解析
(2)3
【分析】（1）根据证明得再证明四边形是平行四边形，最后根据对角线互相垂直的平行四边形是菱形进行证明即可；
（2）过点C作交延长线于点H，求出，再根据菱形的面积计算公式求解即可．
【详解】（1）∵四边形是平行四边形，
∴，
∴
∵O为的中点，
∴
在和中，
，
∴
∴
∴四边形是平行四边形，
∵
∴四边形是菱形，
（2）过点C作交于点H，

∴°，
∵四边形是菱形，
∵，
∴，
∴，
∵，
∴，
∴的面积
【点睛】此题考查了平行四边形的性质，菱形的判定与性质和以及菱形面积求法等知识，熟练掌握相关知识是解题的关键．
11．（2023·北京西城·统考二模）如图，矩形的对角线相交于点O，过点D作的平行线交的延长线于点E．

(1)求证：；
(2)连接，若，，求的长．
【答案】(1)见解析
(2)
【分析】（1）根据矩形的对角线相等可得，对边平行可得，再证明出四边形是平行四边形，根据平行四边形的对边相等可得，从而得证；
（2）如图，过点O作于点F，欲求，只需在直角中求得的值即可．结合三角形中位线求得，结合矩形、平行四边形的性质以及勾股定理求得即可．
【详解】（1）∵四边形是矩形，
∴，
又∵，
∴四边形是平行四边形，
∴，
∴；
（2）如图，过点O作于点F，

∵四边形是矩形，
∴点O是的中点，
∴
∴
∴，
∴点是的中点，
∴是的中位线，
∴
又∵四边形是平行四边形，
∴．
∴．
在中，由勾股定理可得：．
【点睛】本题考查了矩形的性质，平行四边形的判定与性质，熟记各性质并求出四边形是平行四边形是解题的关键．
12．（2023·北京丰台·统考一模）如图，在平行四边形 中，，过点 作 交 的延长线于点 ．
(1)求证：四边形 是矩形；
(2)连接 交 于点 ，连接 ．若 ，，求 的长．
【答案】(1)见解析
(2)
【分析】（1）根据三个角是直角的四边形是矩形判断即可；
（2）先证明是等边三角形，再根据30°的直角三角形的三边关系，利用勾股定理即可计算．
【详解】（1）证明：∵四边形是平行四边形，
∴，
∴，
又∵，
∴，
∴四边形是矩形．
（2）如图所示：
∵四边形是矩形，
∴，
∵四边形是平行四边形，
∴，，
∴，
又∵，
∴是等边三角形，
∴，，，
∴，
在中，
【点睛】本题考查平行四边形的性质，矩形的性质和判定，等边三角形的性质和判定，灵活运用相关性质是解题的关键．
13．（2023·北京海淀·校考二模）如图，在矩形中，，相交于点O，，．
(1)求证：四边形是菱形；
(2)若，求四边形的面积．
【答案】(1)见解析
(2)
【分析】(1)根据矩形的性质得出OA=OB，进而利用菱形的判定解答即可；
(2)根据菱形的性质及面积公式，解直角三角形即可求得．
【详解】（1）证明：，
四边形AEBO是平行四边形
又四边形ABCD是矩形
，，

四边形AEBO是菱形
（2）解：如图：连接EO，交AB于点F
四边形ABCD是矩形
，，

又
是等边三角形，
四边形AEBO是菱形
，

四边形的面积为：
【点睛】本题考查了矩形的性质，菱形的判定与性质，等边三角形的判定与性质，解直角三角形，作出辅助线是解决本题的关键．
14．（2023·北京石景山·统考一模）如图，在中，，，分别为，的中点，过点作交的延长线于点．
(1)求证：四边形是菱形；
(2)若，，求的长．
【答案】(1)见解析
(2)
【分析】（1）根据已知条件得出，，，可得四边形是平行四边形．进而根据已知条件得出，即可得出结论；
（2）连接，得出是等边三角形．在中，解直角三角形即可求解．
【详解】（1）证明：∵，分别为，的中点，
∴，，．
又∵，
∴四边形是平行四边形．
∵，
∴．
∴．
∴四边形是菱形．
（2）解：连接，如图．
∵四边形是菱形，
∴，．
∴是等边三角形．
∵，
∴．
∴．
在中，，，
∴．
【点睛】本题考查了中位线的性质，菱形的性质与判定，解直角三角形，熟练掌握菱形的性质与判定是解题的关键．
15．（2023·北京东城·统考二模）如图，在中，，点为中点，过点分别作的平行线，相交于点．
(1)求证：四边形为矩形；
(2)连接，若，求的长．
【答案】(1)见详解
(2)
【分析】（1）先根据平行四边形的判定，证明四边形是平行四边形，再根据矩形的判定，证明即可；
（2）根据矩形的性质，三角函数，及勾股定理即可得出结果．
【详解】（1）证明：由题意得，
四边形是平行四边形，
，点为中点，
，即，
四边形为矩形；
（2）解：∵四边形为矩形，
，
∵点为中点，
在中，，
解得：
在中，，
故的长为．
【点睛】本题考查了矩形的判定与性质，平行四边形的判定与性质，等腰三角形的性质，平行线的性质，熟练掌握定理与性质是解题的关键．
16．（2023·北京门头沟·统考一模）如图，在菱形中，于E，于F．

(1)求证：四边形是矩形；
(2)连接，如果，，求的长．
【答案】(1)见解析
(2)的长为．
【分析】（1）根据有三个角是直角的四边形是矩形即可得到结论；
（2）设的长为x，由，求得，在中，利用勾股定理列式计算即可求解.
【详解】（1）证明：∵四边形是菱形，
∴，
∵，
∴，
∵，
∴，
∴四边形是矩形；
（2）解：设的长为x，
∵四边形是菱形，
∴，
∵四边形是矩形，
∴，
∵，
∴，
∴，
在中，，，，
由勾股定理得，
解得，
∴的长为．
【点睛】本题考查了菱形的性质，矩形的判定，勾股定理，正切函数，解题的关键是灵活运用所学知识解决问题．
17．（2023·北京通州·统考一模）已知在中，，点D，E分别是边中点，连接，延长到点F，使得，连接．
(1)求证：四边形是菱形
(2)如果，且，求的长．
【答案】(1)见解析
(2)的长为10
【分析】（1）先根据对角线互相平分证明四边形是平行四边形，再根据三角线中位线的性质证明，进而得出，即可证明四边形是菱形；
（2）根据菱形的性质可得，再利用三角函数、勾股定理解即可．
【详解】（1）证明：点E是边中点，
，
又，
四边形是平行四边形
在中，点D，E分别是边中点，
，，
，
，．
四边形是菱形；
（2）解：由（1）知，四边形是菱形，
，
，
，
，
在中，，
，
解得或（舍），
的长为10．
【点睛】本题考查三角形中位线的性质，菱形的判定和性质，利用三角函数、勾股定理解直角三角形等，解题的关键是掌握菱形的判定方法及性质，牢记三角函数的定义．
18．（2023·北京昌平·统考二模）如图，在菱形中，对角线交于点，点是过点作的平行线与过点作的垂线（垂足为）的交点.
(1)求证：四边形是平行四边形；
(2)连接，求证：四边形是矩形.
【答案】(1)见解析
(2)见解析
【分析】（1）根据菱形的性质可得，进而可得，根据两组对边平行的四边形是平行四边形即可证明；
（2）先证四边形是平行四边形，再根据可证四边形是矩形．
【详解】（1）证明：四边形是菱形，
，
又，
，即，
又，
四边形是平行四边形；
（2）证明：四边形是菱形，
，
由（1）得四边形是平行四边形，
，
，
又，
四边形是平行四边形，
，
，
四边形是矩形．
【点睛】本题考查菱形的性质，平行四边形的判定和性质，矩形的判定，解题的关键是掌握菱形的对角线互相平分且垂直．
19．（2023·北京平谷·统考一模）如图，在中，点E是中点．点F是中点．连接平分．
(1)求证：四边形是菱形：
(2)连接，与交于点O，连接．若，，求的长．
【答案】(1)见解析
(2)
【分析】（1）根据四边形ABCD是平行四边形及F是AD中点，E是BC中点，可得四边形AECF是平行四边形，再根据EF平分∠AEC，易证得，则可得，继而证得结论；
（2）过点O作于点G，由三角形面积公式可求的长，勾股定理可求，的长，的长即可求解.
【详解】（1）证明：∵四边形ABCD是平行四边形
∴，
∵F是AD中点，E是BC中点
∴，
∴四边形AECF是平行四边形
∵EF平分∠AEC
∴
∵
∴
∴
∴四边形AECF是菱形
（2）解：∵四边形AECF是菱形
∴，，
∵，，
∴
∴，
过点O作于点G，
∵，
即
∴，
∵
∴，
∴
【点睛】本题考查了平行四边形的性质，菱形的判定和性质，勾股定理的应用，解直角三角形，三角形面积公式的应用，解题的关键是熟练掌握各知识点，作出辅助线，用好数形结合的思想.
20．（2023·北京朝阳·统考二模）如图，在四边形中，，．

(1)求证：四边形为菱形；
(2)若，，求的长．
【答案】(1)见解析
(2)6
【分析】（1）先根据一组对边平行且相等的四边形是平行四边形证明四边形为平行四边形，再由，即可证明平行四边形为菱形；
（2）先证明，进而得到，，利用三角形内角和定理推出，由平行线的性质得到，解，即可得到．
【详解】（1）证明：∵，
∴，
∵，
∴四边形为平行四边形，
又∵，
∴平行四边形为菱形；
（2）解：∵，
∴，
∴，，
∵，
∴，
∴，
∵，
∴，
∴，
在中，，
∴．
【点睛】本题主要考查了菱形的判定，平行线的性质，解直角三角形，等边对等角，三角形内角和定理等等，灵活运用所学知识是解题的关键．
21．（2023·北京·统考一模）如图，四边形中，对角线与相交于点，，，点在上，且．
(1)求证：四边形是菱形；
(2)若，，，求的长．
【答案】(1)见解析
(2)
【分析】（1）先证明，得到，再根据内错角相等，两直线平行，得到，进而证明四边形是平行四边形，然后根据对角线互相垂直，即可证明四边形是菱形；
（2）根据菱形的性质，得到，，再利用勾股定理，求得，然后根据正切值，求得，最后利用勾股定理，得到，即可求出的长．
【详解】（1）证明：在和中，
，
，
，
，
，
四边形是平行四边形，
，，
是等腰三角形，为中点，
，即，
平行四边形是菱形；
（2）解：四边形是菱形，，
，，，
在中，，
，
，
，
，
在中，，
．
【点睛】本题考查了菱形的判定和性质，全等三角形的判定和性质，勾股定理，锐角三角函数等知识，熟练掌握菱形的判定和性质是解题关键．
22．（2023·北京房山·统考一模）如图，中，对角线、交于点，在上截取．
(1)求证：四边形是矩形；
(2)若，求证：平分．
【答案】见解析
【分析】（1）先根据平行四边形的性质得到，进而证明，由此即可证明四边形是矩形；
（2）先证明四边形是正方形，得到，即可证明四边形是菱形，则由菱形的性质可得平分．
【详解】（1）证明：∵四边形是平行四边形，
∴，
∵，
∴，
∴四边形是平行四边形，；
∴四边形是矩形；
（2）证明：∵四边形是矩形，，
∴四边形是正方形，
∴，
又∵四边形是平行四边形，
∴四边形是菱形，
∴平分．
【点睛】本题主要考查了正方形的性质与判定，矩形的判定，菱形的性质与判定，平行四边形的性质，熟知特殊平行四边形的判定定理是解题的关键．
23．（2023·北京朝阳·清华附中校考模拟预测）如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．
（1）求证：四边形BEDF为菱形；
（2）如果∠A=90°，∠C=30°，BD=12，求菱形BEDF的面积．
【答案】(1)见解析
(2)24
【分析】（1）根据平行四边形的和菱形的判定证明即可；
（2）根据含30°的直角三角形的性质和勾股定理以及菱形的面积解答即可．
【详解】证明：（1）∵DE∥BC，DF∥AB，
∴四边形BFDE是平行四边形，
∵BD是△ABC的角平分线，
∴∠EBD=∠DBF，
∵DE∥BC，
∴∠EDB=∠DBF，
∴∠EBD=∠EDB，
∴BE=ED，
∴平行四边形BFDE是菱形；
（2）连接EF，交BD于O，
∵∠BAC=90°，∠C=30°，
∴∠ABC=60°，
∵BD平分∠ABC，
∴∠DBC=30°，
∴BD=DC=12，
∵DF∥AB，
∴∠FDC=∠A=90°，
∴DF=，
在Rt△DOF中，OF=，
∴菱形BFDE的面积=×EF•BD＝×12×4=24．
【点评】此题考查了菱形的判定和性质，熟练掌握菱形的判定和性质是解题的关键．
24．（2023·北京大兴·统考一模）如图，在菱形中，对角线，交于点，延长到点，使得.连接.过点作，交于点，连接
(1)求证：四边形是矩形；
(2)若，，求的长
【答案】(1)见解析
(2)2
【分析】（1）由菱形的性质可知，为的中点，根据，可得为的中位线，可得，进而证得四边形是平行四边形，即可证得四边形是矩形；
（2）结合（1）可知，可证四边形是平行四边形，可得，由，可证得是等边三角形，进而可得答案．
【详解】（1）证明：∵四边形是菱形，
∴，，即：，为的中点，
∵，即为的中点，
∴为的中位线，
∴，
又∵，
∴四边形是平行四边形，
又∵，
∴四边形是矩形；
（2）解：由（1）可知，，四边形是矩形，
∴，则，
∵，
∴四边形是平行四边形，
∴，
∵四边形是菱形，
∴，
∵，
∴是等边三角形，
∴，
∴．
【点睛】本题考查菱形的性质，三角形的中位线定理，矩形的判定及性质，等边三角形的判定及性质，熟练掌握相关性质定理是解决问题的关键．
25．（2023·北京东城·北京市广渠门中学校考二模）如图，的对角线，相交于点，，．
(1)求证：四边形是平行四边形；
(2)当是________（填“矩形”或“菱形”）时，四边形是菱形，并写出证明过程．
【答案】(1)见解析
(2)矩形，证明见解析
【分析】（1）根据平行四边形的性质得到，结合可得，即可证明；
（2）根据矩形的性质得到，再根据有一组邻边相等的平行四边形是菱形判定即可．
【详解】（1）解：在中，，
∵，
∴，
∵，
∴四边形是平行四边形；
（2）矩形，
当是矩形时，，
∴，
∴四边形是菱形．
【点睛】本题考查了平行四边形的判定和性质，矩形的性质，菱形的判定，解题的关键是掌握特殊四边形的判定和性质定理．
26．（2023·北京西城·北师大实验中学校考模拟预测）如图，在▱ABCD中，AC，BD交于点O，且AO＝BO．
（1）求证：四边形ABCD是矩形；
（2）∠ADB的角平分线DE交AB于点E，当AD＝3，tan∠CAB＝时，求AE的长．
【答案】（1）见解析
（2）
【分析】(1)由平行四边形性质和已知条件得出AC＝BD，即可得出结论；
(2)过点E作EG⊥BD于点G，由角平分线的性质得出EG＝EA．由三角函数定义得出AB＝4，sin∠CAB＝sin∠ABD＝，设AE＝EG＝x，则BE＝4﹣x，在Rt△BEG中，由三角函数定义得出，即可得出答案．
【详解】(1)证明：∵四边形ABCD是平行四边形，
∴AC＝2AO，BD＝2BO．
∵AO＝BO，
∴AC＝BD．
∴平行四边形ABCD为矩形．
(2)过点E作EG⊥BD于点G，如图所示：
∵四边形ABCD是矩形，
∴∠DAB＝90°，
∴EA⊥AD，
∵DE为∠ADB的角平分线，
∴EG＝EA．
∵AO＝BO，
∴∠CAB＝∠ABD．
∵AD＝3，tan∠CAB＝，
∴tan∠CAB＝tan∠ABD＝＝．
∴AB＝4．
∴BD＝，sin∠CAB＝sin∠ABD＝．
设AE＝EG＝x，则BE＝4﹣x，
在△BEG中，∠BGE＝90°，
∴sin∠ABD＝．
解得：x＝，
∴AE＝．
故答案为：.
【点睛】本题考查了矩形的判定与性质、角平分线的性质、勾股定理、三角函数定义等知识；熟练掌握矩形的判定与性质和三角函数定义是解题的关键．
27．（2023·北京顺义·统考一模）如图，的对角线，相交于点O，将对角线向两个方向延长，分别至点E和点F，且使．
(1)求证：四边形是平行四边形；
(2)若，求证：四边形是矩形．
【答案】见解析
【分析】（1）由四边形是平行四边形易知，，再证得，即可得出结论．
（2）根据四边形是平行四边形，得，，再根据，得，即可得出结论．
【详解】（1）证明：连接，设与交于点．如图所示：
四边形是平行四边形，
，，
又，
．
四边形是平行四边形．
（2）证明：由(1）知：四边形是平行四边形，
，，
∵
∴
∴四边形是矩形．
【点睛】此题考查了平行四边形的性质，矩形的判定，解题时要注意选择适宜的判定方法．
28．（2023·北京丰台·二模）如图，在中，，点D为的中点，连接，过点C作，且，连接，．

(1)求证：四边形是菱形；
(2)连接，当，时，求的长．
【答案】(1)见解析
(2)
【分析】（1）先证明四边形是平行四边形，再利用直角三角形斜边中线等于斜边一半，得到，即可证明四边形是菱形；
（2）根据菱形的性质，证明四边形是平行四边形，再根据30度角所对的直角边等于斜边一半，推出，进而证明四边形是菱形，然后利用勾股定理，求得的长，即可求出的长．
【详解】（1）证明：，，
四边形是平行四边形，
在中，，点D为的中点，
，
四边形是菱形；
（2）解：四边形是菱形，
，，
，
，
，
四边形是平行四边形，
，，
，
，
，
四边形是菱形，
，，，
在中，，
．

【点睛】本题考查了菱形的判定和性质，直角三角形的特征，勾股定理等知识，熟练掌握菱形的判定和性质是解题关键．
29．（2023·北京延庆·统考一模）如图，在平行四边形中，连接，，点M为边的中点，连接并延长，交的延长线于点E，连接．
(1)求证：四边形是矩形；
(2)若，，求四边形的面积．
【答案】(1)见解析
(2)90
【分析】（1）先根据平行四边形的性质得，．从百得，，再证明．得，从而得四边形是平行四边形．即可由矩形判定定理得出结论，
（2）先由矩形与三角形面积公式求得，．再由求解即可．
【详解】（1）证明：∵四边形是平行四边形，
∴，．
∴，．
∵点M为边的中点，
∴．
∴．
∴．
∴四边形是平行四边形．
∵，
∴．
∴平行四边形是矩形．
（2）解：∵四边形是矩形，
∴，．
∴．
∵，
∴．
∵，
∴．
∴，
．
∴．
【点睛】本题考查平行四边形的性质，矩形的判定和性质，全等三角形的判定与性质，矩形与三角形的面积，熟练掌握平行四边形的性质定理，矩形的判定定理，全等三角形的判定与性质是解题的关键．
30．（2023·北京海淀·北理工附中校考三模）如图，在四边形ABCD中，BD为一条对角线，，，，E为AD的中点，连接BE．
(1)求证：四边形BCDE为菱形；
(2)连接AC，若AC平分，，求AC的长．
【答案】(1)见解析
(2)
【分析】（1）先证明四边形BCDE是平行四边形，再证明一组邻边相等即可；
（2）连接AC，根据平行线的性质及等角对等边证明AB=1，AD=2，可知，再根据菱形的性质即可得出是含的特殊三角形，最后根据勾股定理即可求AC的长．
【详解】（1），E为AD的中点，
，
，
∴四边形BCDE是平行四边形，
，，
，
∴四边形BCDE是菱形．
（2）解：连接AC．
，AC平分，
，
，
，
，
，
四边形BCDE是菱形
，
在中，，
，
．
【点睛】本题考查了菱形的性质与判定，勾股定理等，解题的关键是连接AC构造．
31．（2023·北京门头沟·二模）如图，在中，于E，于F，且．

(1)求证：是菱形；
(2)连接，交于点O，当，时，求的面积．
【答案】(1)见详解
(2)24
【分析】（1）证明，得即可；
（2）在中，根据三角函数求出，再根据勾股定理得的长，然后根据菱形的面积等于对角线乘积的一半即可．
【详解】（1）证明：在中，，
于E，于F，且，
，
∴，
，
∴是菱形；
（2）解：

是菱形，，
，，
，
在中，，
，
的面积为．
【点睛】本题考查了平行四边形的性质，菱形的性质和判定，勾股定理以及解直角三角形等知识，掌握菱形的面积等于对角线乘积的一半是本题的关键．
32．（2023·北京石景山·统考二模）如图，菱形的对角线相交于点，过点作，过点C作交于点．

(1)求证：四边形是矩形；
(2)连接，若，，求的长．
【答案】(1)证明见解析
(2)
【分析】（1）根据菱形的性质可得，再根据，可得四边形是平行四边形，进而证明四边形是矩形；
（2）根据题意可得是等边三角形，勾股定理求得的长，进而求得的长，在中，勾股定理即可求解．
【详解】（1）证明：四边形是菱形，
，
，
四边形是平行四边形，
，
平行四边形是矩形；
（2）解：四边形是菱形，
，
，
是等边三角形，
∴
，
在中，，
∴
，
，
四边形是矩形，
，，
在中，．

【点睛】本题考查了菱形的性质，矩形的性质与判定，含30度角的直角三角形的性质，等边三角形的性质与判定，勾股定理，掌握以上知识是解题的关键．
33．（2023·北京顺义·统考二模）如图，在中，，点关于的对称点为，连接，．

(1)求证：四边形是菱形；
(2)过点A作于E，且交于点F，若，，求的长．
【答案】(1)见解析
(2)
【分析】（1）根据关于的对称点为，可得，，结合已知条件，可得，即可得证；
（2）根据勾股定理求得，根据菱形的性质得出，，即可证明，根据相似三角形的性质即可求解．
【详解】（1）证明：∵关于的对称点为，
∴，，
∵，
∴，
∴四边形是菱形；
（2）解：∵，，
∴，
∴，
∵四边形是菱形，
∴，，
∴，
∴，
∴，
设，，有，
∴，
∴．

【点睛】本题考查了菱形的性质与判定，相似三角形的性质与判定，勾股定理，熟练掌握是菱形的性质与判定解题的关键．
34．（2023·北京西城·北京市第十三中学校考模拟预测）如图，在平行四边形中，过点作于点，的延长线交于点．过点作交于点．交于点．过点作于点．
(1)求证：四边形为矩形；
(2)若，，，求线段的长．
【答案】(1)见解析
(2)40
【分析】（1）根据垂直的定义可得，根据平行线的性质可得，即可证明四边形是矩形；
（2）根据可求出得长，利用勾股定理可求出的长，根据平行四边形的性质可得，利用可证明，可得，根据矩形的性质可得，根据线段的和差关系即可得答案．
【详解】（1）证明：∵，，
∴，
∵，
∴，
∴，
∴四边形是矩形．
（2）解：∵四边形是矩形，，
∴，，
∵，，
∴，
∴，
∵四边形是平行四边形，
∴//，，
∴，
在和中，
，
∴，
∴，
∴．
【点睛】本题考查矩形的判定与性质、平行四边形的性质、全等三角形的判定与性质及解直角三角形，熟练掌握相关性质及判定定理是解题关键．
35．（2023·北京海淀·首都师范大学附属中学校考一模）如图，四边形是平行四边形，相交于点O，点E是的中点，连接，过点E作于点F，过点O作于点G．
(1)求证：四边形是矩形；
(2)若四边形是菱形，，求的长．
【答案】(1)见解析
(2)
【分析】（1）根据平行四边形的性质可知，进而证明是的中位线，得到，再由，，得到，即可证明四边形是矩形；
（2）根据菱形的性质和勾股定理在中求出，然后利用等面积法求出即可．
【详解】（1）证明：∵四边形是平行四边形，
∴，
∵点E是的中点，
∴是的中位线，
∴，
∵，，
∴，
∴四边形是矩形；
（2）解：∵四边形是菱形，
∴，
∵，
∴，
在中，由勾股定理得，
∵，
∴，
∴．
【点睛】本题主要考查了菱形的性质，矩形的判定，三角形中位线定理，勾股定理等等，灵活运用所学知识是解题的关键．
36．（2023·北京海淀·北京交通大学附属中学校考模拟预测）如图，在平行四边形ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．
(1)求证：四边形ABEF是菱形；
(2)若AB＝4，AD＝6，∠ABC＝60°，求tan∠ADP的值．
【答案】(1)见解析
(2)
【分析】（1）根据平行四边形和角平分线的性质可得AB=BE，AB=AF，AF=BE，从而证明四边形ABEF是菱形；
（2）作PH⊥AD于H，由菱形的性质得到AB=AF=4，∠ABF=∠ADB==30°，AP⊥BF，得PH=，AH=1，则DH=5，然后由锐角三角函数的定义求解即可．
【详解】（1）证明：∵四边形ABCD是平行四边形，
∴AD//BC．
∴∠DAE=∠AEB．
∵AE平分∠BAD，
∴∠DAE=∠BAE．
∴∠BAE=∠AEB．
∴AB=BE．
同理：AB=AF．
∴AF=BE．
∴四边形ABEF是平行四边形．
∵AB=BE，
∴四边形ABEF是菱形．
（2）作PH⊥AD于H，如图所示：
∵四边形ABEF是菱形，∠ABC=60°，AB=4，
∴AB=AF=4，∠ABF=∠AFB==30°，AP⊥BF，
∴AP=AB=2，
∴AH=AP=1，PH=，
∴DH=AD-AH=5，
∴tan∠ADP=
【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质、等腰三角形的判定．勾股定理以及三角函数定义等知识；熟练掌握菱形的判定与性质是解题的关键．
37．（2023·北京海淀·校联考模拟预测）如图，在菱形ABCD中，O为AC，BD的交点，P，M，N分别为CD，OD，OC的中点．
(1)求证：四边形OMPN是矩形；
(2)连接AP，若，，求AP的长．
【答案】(1)见解析
(2)
【分析】（1）由三角形中位线定理可得四边形OMPN是平行四边形，再由菱形的性质即可证得结论；
（2）由菱形的性质及已知可得△ABD是等边三角形，进而可得OA的长度，由中位线的性质可得PN及ON，从而可得AN，由矩形的性质及勾股定理即可求得AP的长．
【详解】（1）∵P，M，N分别为CD，OD，OC的中点．
∴，．
∴四边形OMPN是平行四边形．
∵在菱形ABCD中，AC，BD相交于点O，
∴．
∴四边形ONPN是矩形．
（2）∵四边形OMPN是矩形，
∴．
∵四边形ABCD是菱形，
∴，，AC平分∠BAD．
∵，，
∴△ABD是等边三角形．
∴BD=4．
∴，由勾股定理得：．
∴，．
∴．
∴在中,由勾股定理得:．
【点睛】本题考查了菱形的性质，等边三角形的性质，三角形中位线定理，矩形的判定与性质，勾股定理等知识，涉及的知识点较多，灵活运用它们是解题的关键．
38．（2023·北京·校联考一模）如图，四边形的对角线，相交于点O，，为矩形对角线，，．
(1)求证：四边形是菱形；
(2)连接，若，，求的值．
【答案】(1)见解析
(2)
【分析】（1）由矩形的性质可得，，结合可得，结合，可证四边形是平行四边形，再根据可证四边形是菱形；
（2）先根据已知条件和（1）中结论证明是等边三角形，进而求出，，再利用勾股定理解即可．
【详解】（1）证明：四边形是矩形，
，，
，
，
，
四边形是平行四边形．
，
平行四边形是菱形．
（2）解：如图，连接，
四边形是菱形，
，，，
，
，
，
是等边三角形，
，，
，
，
，
四边形是矩形，
，，
．
【点睛】本题考查菱形的判定和性质，等边三角形的判定和性质，矩形的性质，勾股定理解直角三角形等，难度一般，解题的关键是掌握菱形的判定方法．
39．（2023·北京·校考模拟预测）如图，在中，，过点的直线，为边上一点，过点作，交直线于，垂足为，连接，．
(1)求证：．
(2)当，且为中点时，四边形是什么特殊四边形？说明理由．
(3)求∶∶，时，求的长．
【答案】(1)见解析
(2)四边形是正方形，理由见解析
(3)
【分析】（1）证明四边形是平行四边形即可得证；
（2）根据题意证明四边形是平行四边形，根据直角三角形斜边上的中线等于斜边的一半得出，则四边形是菱形，根据已知条件证明，即可得出结论；
（3）根据勾股定理求得，根据平行线分线段成比例得出，根据勾股定理即可求解．
【详解】（1）证明：∵在中，，，
∴，
∵，
∴，
∴四边形是平行四边形，
∴；
（2）四边形是正方形，理由如下，
∵在中，， ，
∴是等腰直角三角形，
∵为的中点，
∴，
∵
∴，
又∵，
∴四边形是平行四边形，
∵，
∴四边形是菱形，
∵，
∴四边形是正方形；
（3）解：∵四边形是平行四边形，
∴，
∵∶∶，，
∴
∴中
∴
∵，
∴
∴，
在中，．
【点睛】本题考查了平行四边形的性质与判定，正方形的性质与判定，平行线分线段成比例，勾股定理，熟练掌握特殊四边形的性质与判定是解题的关键．
40．（2023·北京·校考模拟预测）如图，四边形是矩形，延长至E，使得，连接，过点D作交的延长线于F，连接，．

(1)求证：四边形是菱形；
(2)连接，若，，求的长．
【答案】(1)见详解
(2)
【分析】（1）先证明，即可得、互相垂直平分，问题即可得证；
（2）利用，，可得，即有，根据四边形是菱形，可得，即，再利用勾股定理即可求解．
【详解】（1）∵四边形是矩形，
∴，
∴，
∵，
∴，
∵，，
∴，
∴，
∵，，
∴、互相垂直平分，
∴四边形是菱形；
（2）如图，

∵，，
∴在中，，
∴，
∵四边形是矩形，
∴，，
∵四边形是菱形，
∴，
∴，
∴在中，，
即．
【点睛】本题考查了解直角三角形、菱形的判定与性质，矩形的性质以及勾股定理等知识，掌握菱形的判定与性质，矩形的性质是解答本题的关键．