2024春七下数学第7章一元一次不等式和不等式组7.4综合与实践_排队问题上课课件（沪科版）

这是一份2024春七下数学第7章一元一次不等式和不等式组7.4综合与实践_排队问题上课课件（沪科版），共18页。

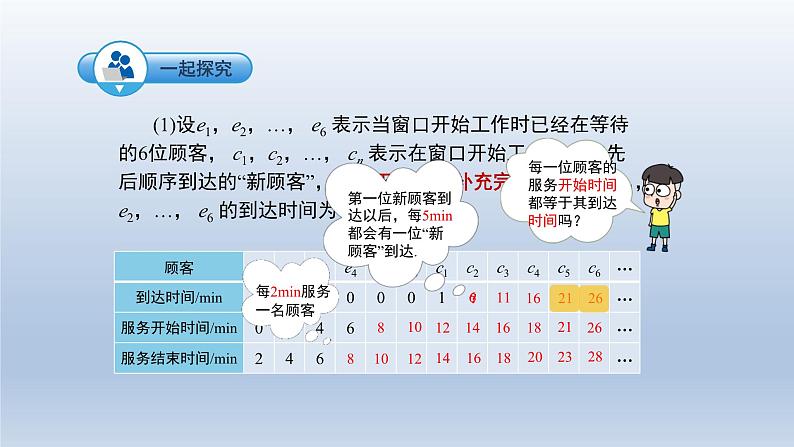
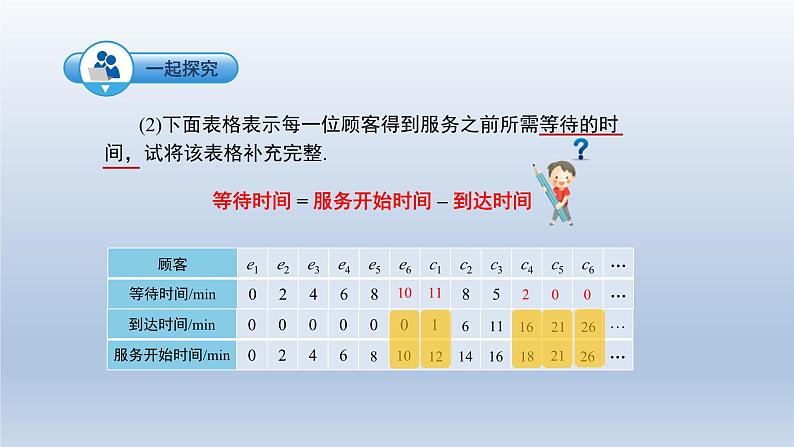
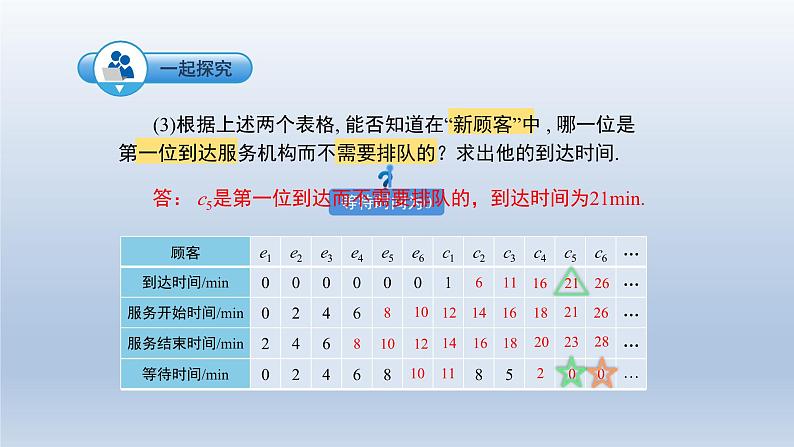
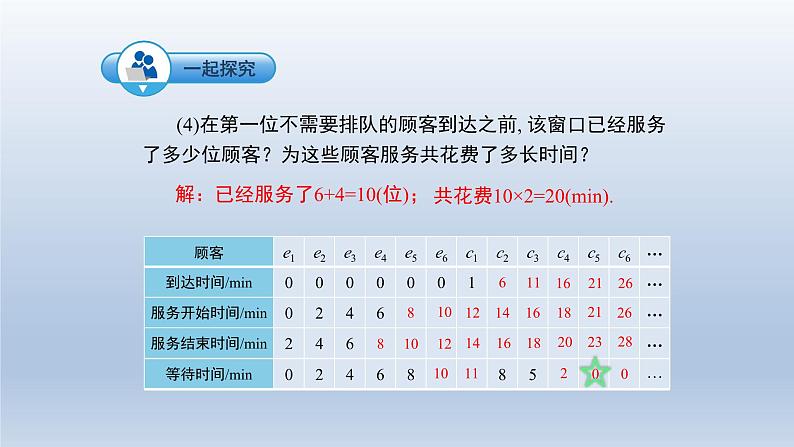
7.3 综合与实践排队问题1.学会运用不等式的相关知识解决实际问题.2.正确地进行分析，建立相应的数学模型，从而培养推理能力.3.初步学会在排队问题中从数学的角度发现问题和提出问题，并综合运用不等式的相关知识和方法解决问题，增强应用意识，提高实践能力.4.培养探索精神以及互相协作的态度，体验数学的应用价值，培养用数学眼光看世界的意识. 在日常生活和生产实践中经常遇到排队等待的现象，如医院挂号付费、银行办理业务、车站购票等. 有时由于排队的人很多，人们将花费很多的时间在等，给他们带来很大影响；如果开设太多窗口又会造成浪费。如何使投入资源较少，而顾客对服务又比较满意，这就需要研究排队问题，下面我们一块来研究最简单的排队问题. (1)设e1，e2，…， e6 表示当窗口开始工作时已经在等待的6位顾客， c1，c2，…， cn 表示在窗口开始工作后，按先后顺序到达的“新顾客”，请将下面表格补充完整(这里假设e1，e2，…， e6 的到达时间为0).881010121214？61416111621261618182021232628 (2)下面表格表示每一位顾客得到服务之前所需等待的时间，试将该表格补充完整.1011200 (3)根据上述两个表格, 能否知道在“新顾客”中 , 哪一位是第一位到达服务机构而不需要排队的？求出他的到达时间. 答： c5是第一位到达而不需要排队的，到达时间为21min. (4)在第一位不需要排队的顾客到达之前, 该窗口已经服务了多少位顾客？为这些顾客服务共花费了多长时间？ 解：已经服务了6+4=10(位)；共花费10×2=20(min).解：(0+2+4+6+8+10+11+8+5+2)÷10=56÷10=5.6(min) (5)平均等待现象是一个重要的服务质量指标，为考察服务质量，问排队现象消失之前，所有顾客的平均等待时间是多少？ 在上述问题中，如果问题的条件变复杂(例如，当窗口开始工作时已经在等待的顾客非常多），使用列表方法就很不方便，你能否用代数式表示出上面的数量，总结上面表格中的数量关系，并根据这个关系来解决问题.解：已经服务了(10+n)位；为这些顾客服务共花费2(10+n)min.解： cn+1的到达时间为(1+5n)min.解：2(10+n)≤1+5n 应用不等式解决排队问题的一般过程：排队问题数学化列不等式数学问题(不等式模型)解不等式检验实际问题的解答 1.2018年国内航空公司规定：旅客乘机时，免费携带行李箱的长、宽、高三者之和不超过115 cm.某厂家生产符合该规定的行李箱．已知行李箱的宽为20 cm，长与高的比为8∶11，则符合此规定的行李箱的高的最大值为________cm.设长为8xcm，则高为11xcm.由题意，得19x+20≤115，解得x≤5，故行李箱的高的最大值为：11x=5555 1. 某次知识竞赛共有20题，答对一题得10分，答错或不答扣5分，小华得分要超过120分，他至少要答对的题数为________．设小华要答对x道.10x5(20x)＞12010x100+5x＞12015x＞220 ∵x为正整数，∴x的最小值是15.即小华至少要答对的题的题数为15.15 2.把一些书分给几名同学，如果每人分3本，那么余8本；如果前面的每名同学分5本，那么最后一人就分不到3本，求这些书本数和人数.设有x名学生，那么共有图书(3x+8)本，则(3x+8)5(x1)≥0(3x+8)5(x1)＜3解得5＜x≤6.5，∴x6， (3x+8)=26答：这些书共有26本，一共有6名同学.列表法和列代数式法