北京市中国人民大学附属中学2023-2024学年七年级上学期期末数学试题（原卷版+解析版）

这是一份北京市中国人民大学附属中学2023-2024学年七年级上学期期末数学试题（原卷版+解析版），文件包含精品解析北京市中国人民大学附属中学2023-2024学年七年级上学期期末数学试题原卷版docx、精品解析北京市中国人民大学附属中学2023-2024学年七年级上学期期末数学试题解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

1. 的倒数是（ ）
A. B. C. D. 5
【答案】B
【解析】
【分析】此题主要考查了倒数的定义．直接利用倒数的定义“两个数乘积是1的数互为倒数”得出答案．
【详解】解：的倒数为．
故选：B．
2. “霜降见霜，谷米满仓”，2023年我国粮食再获丰收．据统计，去年秋粮的种植面积为亿亩，比前年增加了700多万亩，奠定了增产的基础．将1310000000用科学记数法表示应为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了科学记数法的表示方法，科学记数法的表现形式为的形式，其中，为整数，确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，是非负数，当原数绝对值小于1时，是负数，表示时关键是要正确确定的值以及的值．
【详解】解：将1310000000用科学记数法表示应为，
故选：B．
3. 下列各组有理数的大小关系中，正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题主要考查了有理数比较大小，熟知正数大于0，0大于负数，两个负数比较大小，绝对值越大其值越小是解题的关键．
详解】解：A、，原式错误，不符合题意；
B、，原式正确，符合题意；
C、∵，
∴原式错误，不符合题意；
D、，原式错误，不符合题意；
故选B．
4. 方程的解是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题主要考查解一元一次方程，方程两边同除以即可求得答案．
【详解】方程两边同除以，得
．
故选：B
5. 下列运算结果正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据合并同类项法则进行判断即可，此题考查了合并同类项，熟练掌握运算法则是解题的关键．
【详解】解：A．，故选项错误，不符合题意；
B．，故选项正确，符合题意；
C．与不是同类项，不能合并同类项，故选项错误，不符合题意；
D．与不是同类项，不能合并同类项，故选项错误，不符合题意．
故选：B．
6. 若，则下列等式不一定成立的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题主要考查等式基本性质，根据等式的基本性质逐项判断即可．
【详解】A．等式两边都减，得，故本选项不符合题意；
B．等式两边都加，得，故本选项不符合题意；
C．等式两边都乘，得，故本选项符合题意；
D．等式两边都除以，得，故本选项不符合题意．
故选：C．
7. 如图，是线段的中点，是线段的中点，若，则线段的长度为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】本题主要考查了与线段中点有关的计算、线段的和差，由是线段的中点，得出，由是线段的中点得出，最后有计算即可得出答案，找准线段之间的关系是解此题的关键．
【详解】解：是线段的中点，，
，
是线段的中点，
，
，
故选：C．
8. 已知有理数，在数轴上对应点的位置如图所示，那么下列结论正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了利用数轴比较数的大小，有理数绝对值的性质，乘法和加法计算，解题的关键是掌握相关法则并应用．
【详解】解：由数轴可知：，
∴，
故选：D．
9. 如图，在正方形网格中有，两点，点在点的南偏东方向上，且点在点的东北方向上，则点可能的位置是图中的（ ）
A. 点处B. 点处C. 点处D. 点处
【答案】B
【解析】
【分析】本题考查的是方位角的判定，理解方位角的含义是解本题的关键；先画出图形，结合网格特点可得：，，在的东北方向，在的南偏东的方向，再画等边三角形，从而可得答案．
【详解】解：如图，
由网格特点可得：，，在的东北方向，
在的南偏东的方向，
在网格中画等边三角形，，连接并延长，
∴，
∴点可能的位置是图中的，
故选B
10. 一副直角三角板如图1放置：直角三角板的边与直角三角板的边重合，点F在线段的延长线上．如图2，将图1的直角三角板绕点B以每秒的速度顺时针旋转（当射线与射线重合时停止），平分，当满足时，三角板的运动时间为（ ）
A. 31秒B. 秒C. 32秒D. 秒
【答案】B
【解析】
【分析】本题主要考查了几何图形中角度的计算，角平分线的定义，一元一次方程的应用，直角三角板中角度的计算，解题的关键是根据旋转的特点，利用角平分线的定义，列出关于t的方程，解方程即可．
【详解】解：由题意可得：，
∵，，
∴．
∵平分，
∴．
∵，
∴，
解得：．
故选：B．
二、填空题（本题共18分，每小题3分）
11. 如果单项式与是同类项，那么______．
【答案】
【解析】
【分析】本题主要考查了同类项的定义和代数式求值，所含字母相同，相同字母的指数也相同的单项式叫做同类项，据此可得，则．
【详解】解：∵单项式与是同类项，
∴，
∴，
故答案为：．
12. 若关于的一元一次方程的解为正数，则的一个取值可以为______．
【答案】（答案不唯一）
【解析】
【分析】本题主要考查了解一元一次方程，先解方程得到，再由方程的解为正数得到，据此可得答案．
【详解】解：解方程得，
∵关于的一元一次方程的解为正数，
∴，
∴，
∴的一个取值可以为，
故答案为：（答案不唯一）．
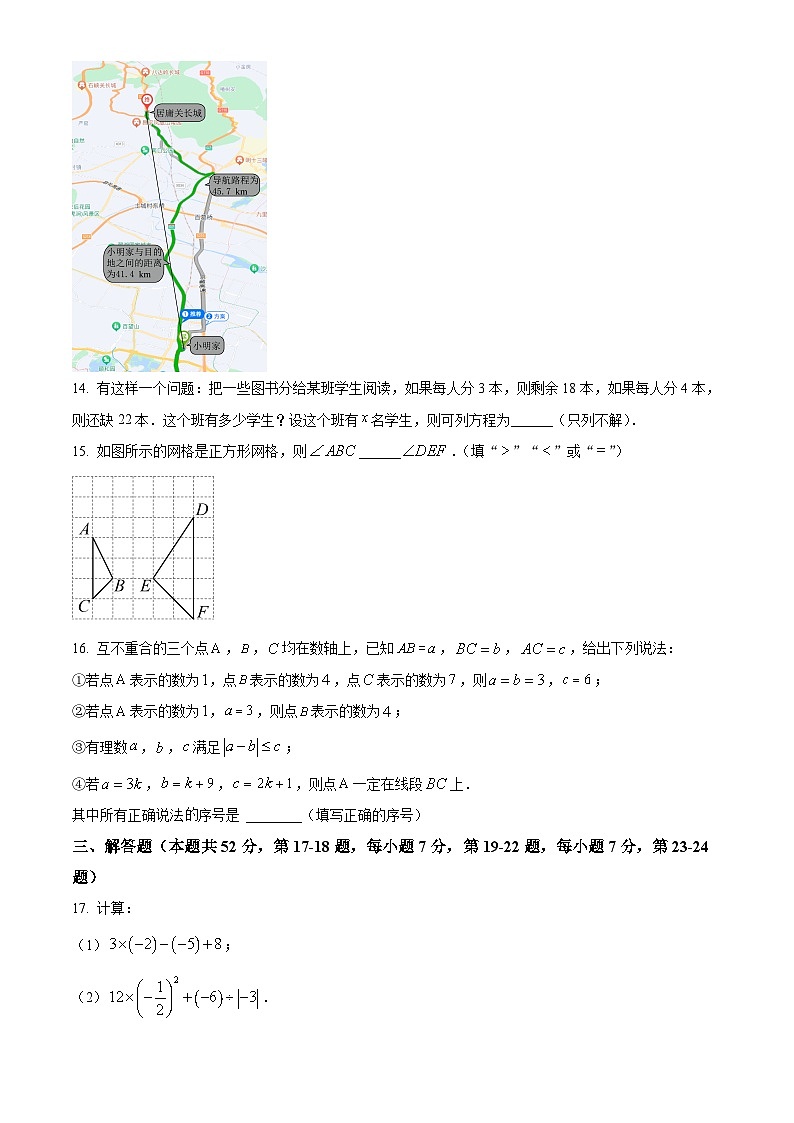
13. 小明一家准备自驾去居庸关长城游玩．出发前，爸爸用地图软件查到导航路程为，小明用地图软件中的测距功能测出他家和目的地之间的距离为，如图所示，小明发现他测得的距离比爸爸查到的导航路程少．请你用所学数学知识说明其中的道理：______．
【答案】两点之间，线段最短
【解析】
【分析】本题考查了线段的性质，根据两点之间，线段最短即可得出答案，熟练掌握线段的性质是解此题的关键．
【详解】解：由题意可得：其中的道理为两点之间，线段最短，
故答案为：两点之间，线段最短．
14. 有这样一个问题：把一些图书分给某班学生阅读，如果每人分3本，则剩余18本，如果每人分4本，则还缺22本．这个班有多少学生？设这个班有名学生，则可列方程为______（只列不解）．
【答案】
【解析】
【分析】本题考查了由实际问题抽象出一元一次方程，设这个班有名学生，根据图书数量不变，列出一元一次方程，即可得出答案，理解题意，找准等量关系是解此题的关键．
【详解】解：设这个班有名学生，
由题意得：，
故答案为：．
15. 如图所示的网格是正方形网格，则______．（填“”“”或“”）
【答案】
【解析】
【分析】本题主要考查了角的比较，根据，即可得到结论．
【详解】解：如图所示，，
∴，
故答案为：．
16. 互不重合的三个点，，均在数轴上，已知，，，给出下列说法：
①若点表示的数为，点表示的数为，点表示的数为，则，；
②若点表示的数为，，则点表示的数为；
③有理数，，满足；
④若，，，则点一定在线段上．
其中所有正确说法的序号是 ________（填写正确的序号）
【答案】①③④
【解析】
【分析】本题主要考查数轴、线段：
①可知，，，即可判断说法是否正确；
②可知，即可判断说法是否正确；
③，，的关系可能情形为：，，，分类讨论，即可判断说法是否正确；
④分三种情况讨论：当点在上时，当点在上时，当点在上时，即可判断说法是否正确．
【详解】①若表示数为，表示数为，表示数为，
则，，．
故①正确
②若表示数为，，则
，
∴．
∴或．
∴表示数为或．
故②错误，
③，，的关系可能情形为：，，．
当或时，，
当时，，
∴．
故③正确，
④若，，，且．
当点在上时，则有，即
．
化简得：，不成立．
当点在上时，则有，即
．
化简得，不成立．
当点在上时，则有，即
．
化简得，
解得．
∴点定在线段上．
故④正确．
故答案为：①③④．
三、解答题（本题共52分，第17-18题，每小题7分，第19-22题，每小题7分，第23-24题）
17. 计算：
（1）；
（2）．
【答案】（1）7 （2）1
【解析】
【分析】本题考查了有理数的混合运算，熟练掌握运算法则以及运算顺序是解此题的关键．
（1）根据有理数的混合运算法则计算即可得出答案；
（2）先计算乘方与绝对值，再计算乘除，最后计算加减即可．
【小问1详解】
解：；
【小问2详解】
解：．
18. 解下列方程：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题主要考查了解一元一次方程，熟知解一元一次方程的步骤是解题的关键．
（1）按照去括号，移项，合并同类项，系数化为1的步骤解方程即可；
（2）按照去分母，去括号，移项，合并同类项，系数化为1的步骤解方程即可．
【小问1详解】
解：
去括号得：，
移项得：，
合并同类项得：，
系数化为1得：；
【小问2详解】
解：
去分母得：，
去括号得：，
移项得：，
合并同类项得：
系数化为1得：．
19 先化简求值：，其中．
【答案】，
【解析】
【分析】本题考查整式的化简求值，熟练掌握相关运算法则是解题的关键，将原式去括号，合并同类项后代入数值计算即可．
【详解】解：原式
；
当时，
原式．
20. 如图，已知，点在射线上．
（1）请按照下列步骤画图(保留作图痕迹)：
①用圆规射线上取一点，使；
②在内部作射线，使；
③在射线上取一点(不与点重合)，连接，；
（2）由图可知， (填“”“”或“”)．
【答案】（1）见解析 （2）
【解析】
【分析】本题主要考查基本的几何图形：
（1）按要求作图即可；
（2）根据线段比较的方法，借助圆规，即可求得答案．
【小问1详解】
如图所示：
【小问2详解】
借助圆规可知，．
故答案为：
21. 如图，，是内部的两条射线，，，与互为补角，求的度数．
【答案】
【解析】
【分析】本题主要考查了几何图形中角度的计算，补角的定义，根据度数之和为180度的两个角互为补角得到，进而推出，则．
【详解】解：∵与互为补角，
∴，
∵，，
∴，
∵，，
∴，
∴．
22. 如图，点C，D在线段上，，，D为线段的中点．
（1）求线段的长；
（2）若E是直线上一点，且，求线段的长．
【答案】（1）5 （2）7或17
【解析】
【分析】本题考查线段中点的有关计算，线段的和差关系，注意分情况讨论是解题的关键．
（1）先计算出，再根据线段中点的定义求解；
（2）分E在A的左侧、右侧两种情况，利用线段的和差关系分别求解即可．
【小问1详解】
解：，
∵D为线段的中点，
∴；
【小问2详解】
解：∵，
∴，
若E在A的左侧，则，
若E在A的右侧，则，
∴线段的长为17或7．
23. 故宫文物医院（故宫博物院文保科技部）传承了历史悠久的传统文物修复技艺，掌握了先进的现代科学技术，拥有上百位从事各类文物保护修复与研究的优秀专业技术人才，是一所名副其实的、的现代科学理念和架构的“文物综合性医院”．半个多世纪以来，许多国宝在这里得以延年益寿．文物修复师们计划用30个月完成某件文物的修复工作．如果让一名文物修复师单独修复该文物．需要720个月完成．假设每名文物修复师的工作效率相同，先由16名文物修复师一起修复了10个月，还需要增加多少名文物修复师才能按时完成修复工作？

【答案】还需要增加12名文物修复师才能按时完成修复工作
【解析】
【分析】本题主要考查了一元一次方程的实际应用，设还需要增加名文物修复师才能按时完成修复工作，根据工作总量工作时间工作效率列出方程求解即可．
【详解】解：设还需要增加名文物修复师才能按时完成修复工作．
依题意列方程，得．
解得．
答：还需要增加12名文物修复师才能按时完成修复工作．
24. 定义一种新运算“&”：当时，；当时，；当时，．例如：．
（1）直接写出 ；
（2）已知，求的值；
（3）若关于方程的解为，则的值为 ．
【答案】（1）
（2）2或
（3）
【解析】
【分析】本题考查了有理数的加法、解一元一次方程，理解题意，采用分类讨论的思想，准确进行计算是解此题的关键．
（1）由得出，即可得解；
（2）分三种情况：当时，当时，当时，分别得出一元一次方程，解方程即可得出答案；
（3）由题意可得，从而得出，解方程即可得出答案．
【小问1详解】
解：，
，
故答案为：；
【小问2详解】
解：当时，，即，
解得：；
当时，，即，
解得：；
当时，，即，
解得：（不符合题意，舍去）；
综上所述，的值为2或；
【小问3详解】
解：，
，
，即，
解得：，
故答案为：．
25. 已知为直线上一点，射线，，位于直线的上方，，，在的左侧．
（1）如图1，若，则 ；
（2）已知，射线平分．
①如图2，当时，猜想与之间的数量关系，并证明；
②射线在直线的下方，且满足，射线平分，当与互余时，直接写出的度数为 ．
【答案】（1）
（2）①，理由见解析；②
【解析】
【分析】本题主要考查角平分线的定义、余角和补角:
（1）根据，即可求得答案；
（2）①根据，，，进而可求得；
②根据，可求得，，然后分两种情况：和．
【小问1详解】
∵，，，，
∴．
故答案为：
【小问2详解】
①由题可得射线平分，则，
又∵，，，，
∴．
∴．
②∵与互余，
∴．
∵射线平分，
∴．
又∵，，
∴．
∴．
∵射线在直线的下方，
∴．
∴．
当时，如图所示．
由（2）①得，
又∵，
∴．
∴．
当时，如图所示．
∵，
∴．
∴．
∴．
综上所述，的度数为．
故答案为：．
26. 在数轴上，把原点记作点，点和点分别表示的数为，，我们称关于的一元一次方程为线段的相关方程，将方程的解记为，在数轴上对应的点为，若点在线段上，则称线段为美好线段，为线段的美好点．
（1）若，，则线段的相关方程为 ；线段是否是美好线段 （填“是”或“否” ；
（2）已知，若线段的美好点恰好是线段的中点，求点表示的数；
（3）已知数组，，，，，，，，一共有4047个数，数组，，0，1，2，3，4，5，6，7，一共有10个数．有理数是数组中的一个数，有理数是数组中的一个数，若线段为美好线段，且线段的美好点在数轴的正半轴上，则这样的美好点一共有 个．
【答案】26. ，是
27.
28. 46
【解析】
【分析】本题考查了定义新运算，一元一次方程的解，数轴上的点
（1）由题意和美好线段的定义可得答案；
（2）由线段的美好点恰好是线段的中点，得，将代入计算可得，即可求出点表示的数；
（3）根据一元一次方程的定义求出，再解得，分两种情况或，当时，解得；当时，解得，即可得美好点数．
【小问1详解】
解：由题意可知线段的相关方程为
，
解得：，
，
线段是美好线段；
故答案为：；是．
【小问2详解】
解：由题意可知：，
，
解得：，
，
点表示的数是；
【小问3详解】
解：是关于的一元一次方程，
，
解方程，
解得：，
即，
点在线段上，
，即，
，
解得：，
，
，
或，
因为美好点在数轴的正半轴上，即，
所以，
当时，，
即，
解得：，所以，
，即，
解得：，
所以，
所以可取，，，，共8个；
当时，，所以，
解得：，
所以，
，
即，
解得：，
所以，
所以可取，，，，共38个，
，
美好点一共有46个；
故答案为：46．