数学七年级上册6.4 平行测试题

这是一份数学七年级上册6.4 平行测试题，共18页。

本试卷满分100分，考试时间40分钟，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
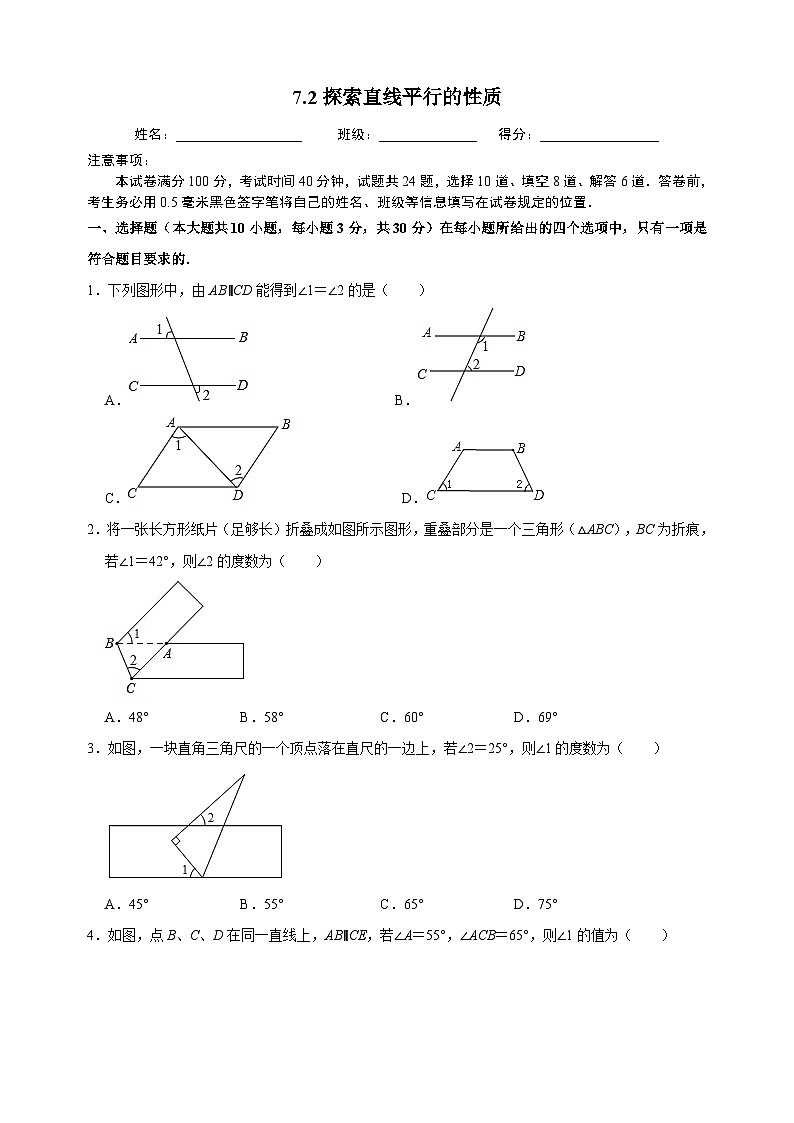
1．下列图形中，由AB∥CD能得到∠1＝∠2的是（ ）
A． B．
C． D．
2．将一张长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形（△ABC），BC为折痕，若∠1＝42°，则∠2的度数为（ ）
A．48°B．58°C．60°D．69°
3．如图，一块直角三角尺的一个顶点落在直尺的一边上，若∠2＝25°，则∠1的度数为（ ）
A．45°B．55°C．65°D．75°
4．如图，点B、C、D在同一直线上，AB∥CE，若∠A＝55°，∠ACB＝65°，则∠1的值为（ ）
A．80°B．65°C．60°D．55°
5．如图，直线a、b被直线c所截，a∥b，若∠1＝40°，则（ ）
A．∠2＝50°B．∠3＝50°C．∠4＝160°D．∠5＝40°
6．如图，点A在直线DE上，AB∥DC，量得∠D＝∠B＝70°，下列结论不正确的是（ ）
A．AD∥BCB．∠DAF＝70°C．∠C＝110°D．∠EAF＝2∠B
7．如图，给出下列条件：
①∠1＝∠2；
②∠3＝∠4；
③∠B＝∠DCE；
④AD∥BC且∠B＝∠D．
其中，能推出AB∥DC的条件共有（ ）
A．1个B．2个C．3个D．4个
8．如图，将长方形纸片ABCD沿EF折叠后，点D、C分别落在点D'、C'的位置，D'C'与
BF交于点G．若∠EFG＝68°，则∠1的度数为（ ）
A．44°B．46°C．60°D．68°
9．如图，a∥b，将直角三角尺的两个锐角顶点分别落在a、b上．若∠1＝70°，则∠2等于（ ）
A．10°B．15°C．20°D．30°
10．如图，直线a∥b，直线c与直线a、b分别交于点M、N，射线PN⊥c，则图中∠1与∠2一定满足的关系是（ ）
A．同位角B．相等C．互余D．互补
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
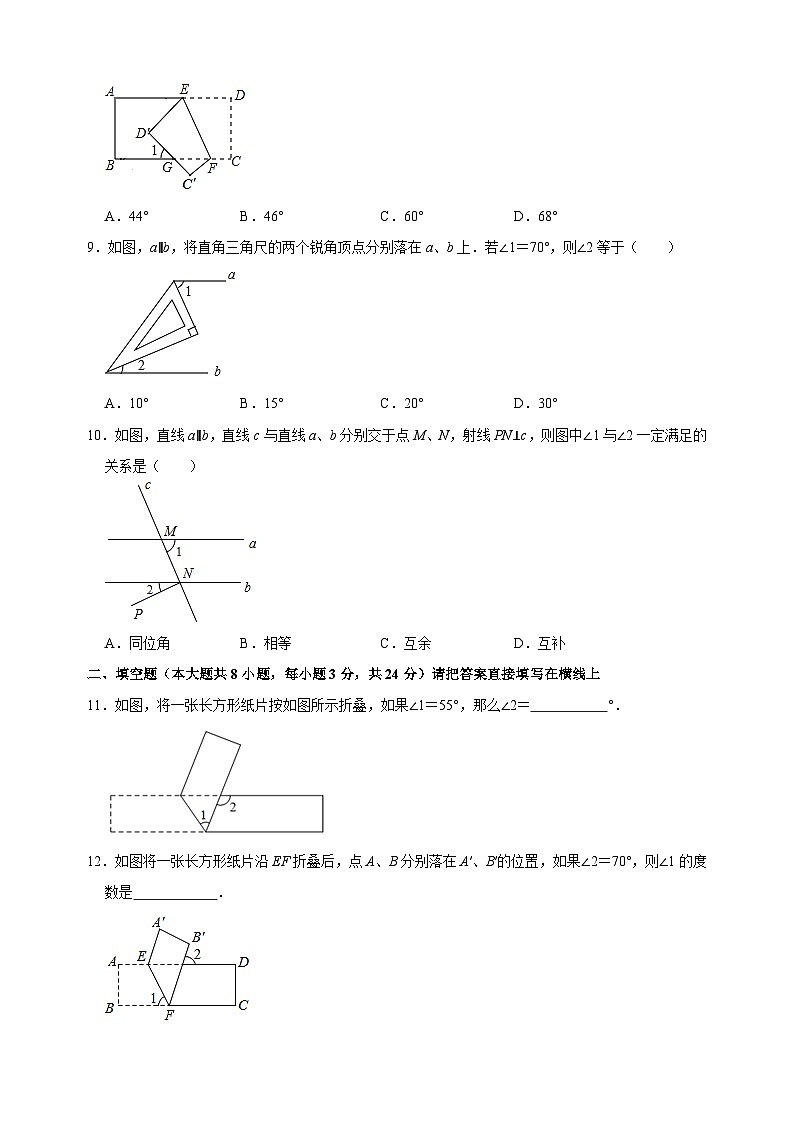
11．如图，将一张长方形纸片按如图所示折叠，如果∠1＝55°，那么∠2＝ °．
12．如图将一张长方形纸片沿EF折叠后，点A、B分别落在A′、B′的位置，如果∠2＝70°，则∠1的度数是 ．
13．如图，如果∠1＝∠3，∠2＝64°，那么∠4的度数为 ．
14．如图，已知：DE∥BC，∠A＝65°，∠C＝55°，则∠1＝ ．
15．如图，直线a，b被直线c所截，a∥b，若∠2＝40°，则∠1等于 ．
16．如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED＝90°，则∠BFD＝ ．
17．如图，AB∥CD，AD∥BC，过点D作DE⊥BC，交BC延长线于点E，若∠B＝48°，则∠1＝ °．
18．如图，l1∥l2，AB⊥l1，垂足为O，BC交l2于点E，若∠ABC＝125°，则∠1＝ °．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．填写下列推理中的空格：
已知：如图，点E在CD上，且BE平分∠ABC，∠1＝∠2．
求证：∠BAD+∠ADE＝180°．
证明：∵BE平分∠ABC（已知），
∴∠EBA＝∠ （ ）．
又∵∠1＝∠2（已知），
∴∠2＝∠ （ ），
∴AB∥ （ ），
∴∠BAD+∠ADE＝180°（ ）．
20．在下列解题过程的空白处填上适当的推理理由或数学表达式：
如图，在△ABC中，已知∠ADE＝∠B，∠1＝∠2，FG⊥AB于点G．
求证：CD⊥AB．
证明：∵∠ADE＝∠B（已知），
∴DE∥BC（ ），
∵DE∥BC（已证），
∴ ，（ ）
又∵∠1＝∠2（已知），
∴ ，（ ）
∴CD∥FG（同位角相等，两直线平行），
∴∠CDB＝∠FGB（两直线平行，同位角相等），
∵FG⊥AB（已知），
∴∠FGB＝90°（垂直的定义）．
∴∠CDB＝90°
∴CD⊥AB（垂直的定义）．
21．如图，点D、E、F分别是△ABC三边上的点，DF∥AC，∠BFD＝∠CED，请写出∠B与∠CDE之间的数量关系，并说明理由．
22．已知：如图，AB∥CD，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1＝∠A．
（1）求证：FE∥OC；
（2）若∠BFE＝110°，∠A＝60°，求∠B的度数．
23．如图，已知AB∥CD，∠1＝∠2，CF平分∠DCE．
（1）试判断直线AE与BF有怎样的位置关系？并说明理由；
（2）若∠1＝80°，求∠3的度数．
24．如图，在△ABC中，点D、E分别在BC、AB上，且EF∥AD，∠1+∠2＝180°．
（1）试猜想∠2与∠BAD的关系，并说明理由；
（2）若DG平分∠ADC，求证：DG∥AB．
参考答案
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．【分析】根据平行线的性质求解即可求得答案，注意掌握排除法在选择题中的应用．
【解析】A、∵AB∥CD，
∴∠1＝∠3，
∵∠2＝∠3，
∴∠1＝∠2，故A正确；
B、∵AB∥CD，
∴∠1+∠2＝180°，故A错误；
C、∵AB∥CD，
∴∠BAD＝∠CDA，
若AC∥BD，可得∠1＝∠2；故C错误；
D、若梯形ABCD是等腰梯形，可得∠1＝∠2，故D错误．
故选：A．
2． 【分析】根据平行线的性质，可以得到∠1＝∠4，∠4＝∠5，再根据∠1＝42°和折叠的性质，即可得到∠2的度数，本题得以解决．
【解析】如右图所示，
∵长方形的两条长边平行，∠1＝42°，
∴∠1＝∠4＝42°，∠4＝∠5，
∴∠5＝42°，
由折叠的性质可知，∠2＝∠3，
∵∠2+∠3+∠5＝180°，
∴∠2＝69°，
故选：D．
3． 【分析】根据平行线的性质和直角三角形的性质，可以得到∠1的度数，本题得以解决．
【解析】过直角顶点作直尺长边的平行线，如右图所示，
则∠2＝∠3，∠1＝∠4，
∵∠2＝25°，
∴∠3＝25°，
∵∠3+∠4＝90°，
∴∠4＝65°，
∴∠1＝65°，
故选：C．
4． 【分析】首先根据三角形内角和定理求得∠B的度数，然后根据平行线的性质解答．
【解析】如图，∵∠A＝55°，∠ACB＝65°，
∴∠B＝180°﹣55°﹣65°＝60°．
∵AB∥CE，
∴∠1＝∠B＝60°．
故选：C．
5． 【分析】根据两直线平行，同位角相等；对顶角相等；邻补角互补即可求解．
【解析】∵a∥b，
∴∠2＝∠1＝40°，
由对顶角相等得∠3＝∠1＝40°，
由邻补角互补得∠4＝180°﹣∠1＝140°，
由对顶角相等得∠5＝∠2＝40°，
故正确的是D选项．
故选：D．
6．【分析】由平行线的判定与性质分别对各个选项进行判断即可．
【解析】∵AB∥DC，
∴∠D＝∠BAE，∠DAF＝∠B＝70°，选项B不符合题意，
∵∠D＝∠B＝70°，
∴∠B＝∠BAE＝70°，
∴AD∥BC，选项A不符合题意；
∴∠C+∠D＝180°，
∴∠C＝110°，选项C不符合题意；
∵∠EAF＝180°﹣∠DAF＝110°，∠B＝70°，
∴∠EAF≠2∠B，选项D符合题意；
故选：D．
7．【分析】根据平行线的判定与性质进行逐一推理即可．
【解析】①∵∠1＝∠2，
∴AB∥CD（内错角相等，两直线平行），
所以①正确；
②∵∠3＝∠4，
∴AD∥BC，
所以②错误；
③∵∠B＝∠DCE，
∴AB∥CD（同位角相等，两直线平行），
所以③正确；
④∵AD∥BC，
∴∠B+∠BAD＝180°，
∵∠B＝∠D，
∴∠D+∠BAD＝180°，
∴AB∥CD（同旁内角互补，两直线平行），
所以④正确．
其中，能推出AB∥DC的条件共有①③④3个．
故选：C．
8．【分析】由平角的性质可得∠EFC＝112°，由折叠的性质可得∠EFC＝∠EFC'＝112°，∠C'＝∠C＝90°，由直角三角形的性质可求解．
【解析】∵∠EFG＝68°，
∴∠EFC＝112°，
∵将长方形纸片ABCD沿EF折叠，
∴∠EFC＝∠EFC'＝112°，∠C'＝∠C＝90°，
∴∠GFC'＝∠EFC'﹣∠EFG＝44°，
∴∠FGC'＝90°﹣∠FGC'＝46°，
故选：B．
9．【分析】根据平行线的性质和直角三角形的性质，可以得到∠2的度数，本题得以解决．
【解析】∵a∥b，
∴∠1+∠3+∠4+∠2＝180°，
∵∠3+∠4＝90°，∠1＝70°，
∴∠2＝20°，
故选：C．
10．【分析】根据平行线的性质得出∠1＝∠3，求出∠2+∠3＝90°，再得出选项即可．
【解析】∵射线PN⊥c，
∴∠MNP＝90°，
∵a∥b，
∴∠1＝∠3，
∴∠1+∠2＝∠3+∠2＝∠MNP＝90°，
即∠1与∠2互余，
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．【分析】根据平行线的性质和折叠的性质，可以得到∠2的度数，本题得以解决．
【解析】由折叠的性质可得，∠1＝∠3，
∵∠1＝55°，
∴∠1＝∠3＝55°，
∵长方形纸片的两条长边平行，
∴∠2＝∠1+∠3，
∴∠2＝110°，
故答案为：110．
12．【分析】根据平行线的性质，可以得到∠2＝∠CFB'，从而可以得到∠BFB′的度数，然后即可得到∠1的度数．
【解析】∵AD∥BC，∠2＝70°，
∴∠2＝∠CFB'＝70°，
∴∠BFB′＝110°，
由折叠知，∠1＝∠EFB'∠BFB'＝55°，
故答案为：55°．
13．【分析】根据∠1＝∠3，可以得到AB∥CD，从而可以得到∠2＝∠5，再根据∠5+∠4＝180°，即可得到∠4的度数．
【解析】∵∠1＝∠3，
∴AB∥CD，
∴∠2＝∠5，
∵∠2＝64°，
∴∠5＝64°，
∵∠5+∠4＝180°，
∴∠4＝116°，
故答案为：116°．
14．【分析】根据平行线的性质和三角形内角和，可以求得∠1的度数．
【解析】∵DE∥BC，∠C＝55°，
∴∠C＝∠AED＝55°，
∵∠A＝65°，
∴∠1＝180°﹣∠A﹣∠AED＝180°﹣65°﹣55°＝60°，
故答案为：60°．
15．【分析】根据平行线的性质，可以得到∠3的度数，再根据∠1+∠3＝180°，即可得到∠1的度数．
【解析】∵a∥b，∠2＝40°，
∴∠2＝∠3＝40°，
∵∠1+∠3＝180°，
∴∠1＝140°，
故答案为：140°．
16．【分析】根据平行线的性质和角平分线的性质，可以求得∠BFD的度数，本题得以解决．
【解析】∵AB∥CD，
∴∠ABE＝∠4，∠1＝∠2，
∵∠BED＝90°，∠BED＝∠4+∠EDC，
∴∠ABE+∠EDC＝90°，
∵BF平分∠ABE，DF平分∠CDE，
∴∠1+∠3＝45°，
∵∠5＝∠2+∠3，
∴∠5＝∠1+∠3＝45°，
即∠BFD＝45°，
故答案为：45°．
17．【分析】根据平行线的性质和垂线的定义即可求解．
【解析】∵AB∥CD，
∴∠DCE＝∠B＝48°，
∵DE⊥BC，
∴∠DEC＝90°，
∴∠1＝90°﹣48°＝42°．
故答案为：42．
18．【分析】过B作BF∥l2，利用平行线的性质可得∠1＝∠FBC，然后求出∠FBC的度数即可．
【解析】过B作BF∥l2，
∵l1∥l2，
∴BF∥l1∥l2，
∴∠ABF＝∠2，∠1＝∠FBC，
∵AB⊥l1，
∴∠2＝90°，
∴∠ABF＝90°，
∵∠ABC＝125°，
∴∠FBC＝35°，
∴∠1＝35°，
故答案为：35．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19． 证明：∵BE平分∠ABC（已知），
∴∠EBA＝∠ 1 （ 角平分线的定义 ）．
又∵∠1＝∠2（已知），
∴∠2＝∠ EBA （ 等量代换 ），
∴AB∥ CD （ 内错角相等，两直线平行 ），
∴∠BAD+∠ADE＝180°（ 两直线平行，同旁内角互补 ）．
【分析】利用角平分线的定义，平行线的性质定理和性质定理解答即可．
【解析】证明：∵BE平分∠ABC（已知），
∴∠EBA＝∠1（角平分线的定义）．
又∵∠1＝∠2（已知），
∴∠2＝∠EBA（等量代换），
∴AB∥CD（内错角相等，两直线平行），
∴∠BAD+∠ADE＝180°（两直线平行，同旁内角互补）．
故答案为：1；角平分线的定义；EBA；等量代换；CD；内错角相等，两直线平行；两直线平行，同旁内角互补．
20． 证明：∵∠ADE＝∠B（已知），
∴DE∥BC（ 同位角相等，两直线平行 ），
∵DE∥BC（已证），
∴ ∠1＝∠DCB ，（ 两直线平行，内错角相等 ）
又∵∠1＝∠2（已知），
∴ ∠DCB＝∠2 ，（ 等量代换 ）
∴CD∥FG（同位角相等，两直线平行），
∴∠CDB＝∠FGB（两直线平行，同位角相等），
∵FG⊥AB（已知），
∴∠FGB＝90°（垂直的定义）．
∴∠CDB＝90°
∴CD⊥AB（垂直的定义）．
【分析】根据平行线的判定和性质，结合证明过程求解即可．
【解析】证明：∵∠ADE＝∠B（已知），
∴DE∥BC（同位角相等，两直线平行），
∵DE∥BC（已证），
∴∠1＝∠DCB，（两直线平行，内错角相等）
又∵∠1＝∠2（已知），
∴∠DCB＝∠2，（等量代换）
∴CD∥FG（同位角相等，两直线平行），
∴∠CDB＝∠FGB（两直线平行，同位角相等），
∵FG⊥AB（已知），
∴∠FGB＝90°（垂直的定义）．
∴∠CDB＝90°
∴CD⊥AB（垂直的定义）．
故答案为：同位角相等，两直线平行；∠1＝∠DCB；两直线平行，内错角相等；∠DCB＝∠2；等量代换．
21．【分析】根据平行线的性质和判定，可以得到∠B与∠CDE之间的数量关系．
【解析】∠B＝∠CDE，
理由：∵DF∥AC，
∴∠DFB＝∠A，
∵∠BFD＝∠CED，
∴∠A＝∠CED，
∴AB∥DE，
∴∠B＝∠CDE．
22．【分析】（1）由平行线的性质得∠A＝∠C，由∠1＝∠A，得∠C＝∠1，即可得出结论；
（2）由平行线的性质得∠BFE+∠DOC＝180°，求出∠DOC＝70°，由对顶角相等得∠AOB＝∠DOC＝70°，由三角形内角和定理即可得出答案．
【解析】（1）证明：∵AB∥CD，
∴∠A＝∠C（两直线平行，内错角相等），
又∵∠1＝∠A，
∴∠C＝∠1，
∴FE∥OC（同位角相等，两直线平行）；
（2）解：∵FE∥OC，
∴∠BFE+∠DOC＝180°（两直线平行，同旁内角互补），
又∵∠BFE＝110°，
∴∠DOC＝70°，
∴∠AOB＝∠DOC＝70°，
∴∠B＝180°﹣∠A﹣∠AOB＝180°﹣60°﹣70°＝50°．
23．【分析】（1）由平行线的性质得∠2＝∠CDF．证出∠1＝∠CDF，即可得出AE∥BF；
（2）求出∠ECD＝100°，由角平分线定义得∠ECF＝50°，再由平行线的性质即可得出结论．
【解析】（1）AC∥BD．理由如下：
∵AB∥CD，
∴∠2＝∠CDF，
∵∠1＝∠2，
∴∠1＝∠CDF，
∴AE∥BF；
（2）∵∠1＝80°，
∴∠ECD＝180°﹣∠1＝180°﹣80°＝100°，
∵CF平分∠ECD，
∴∠ECF∠ECD＝50°．
∵AC∥BD，
∴∠3＝∠ECF＝50°．
24．【分析】（1）由平行线的性质和∠1+∠2＝180°，可推出∠2与∠BAD的关系；
（2）由（1）的结论和DG平分∠ADC，可得∠ADG与∠BAD的关系，利用平行线的判定得结论．
【解析】证明：（1）∠2与∠BAD相等．
理由：∵EF∥AD，
∴∠1+∠BAD＝180°．
∵∠1+∠2＝180°．
∴∠2＝∠BAD．
（2）∵DG平分∠ADC，
∴∠2＝∠ADG．
由（1）知∠2＝∠BAD，
∴∠ADG＝∠BAD．
∴DG∥AB．