



2024年中考数学压轴题专项练习—中点四边形模型
展开1、以专题复习为主。如选择题、填空题的专项练习,要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习,深化对常考题型的熟悉程度。在函数复习过程中,如果考生未能完全理解简单实例中的数量关系和变化规律,针对此类问题,在专项复习中,可以通过选择题、填空题的专项练习,进行突破,如“读懂图象信息问题”等,将复杂问题由浅入深,层层分解,提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法,要通过典型试题的训练,进一步渗透和深刻理解其内涵,重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度,培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来,通过一题多解,积极地探求解决问题的最优解法,这样,对于解决难度较大的压轴题会有很大的帮助。
中点四边形
1.(2022春•怀仁市期中)已知:如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形(即四边形的中点四边形).
(1)四边形的形状是 ,证明你的结论.
(2)当四边形的对角线满足 条件时,四边形是矩形.
(3)你学过的哪种特殊四边形的中点四边形是菱形? .
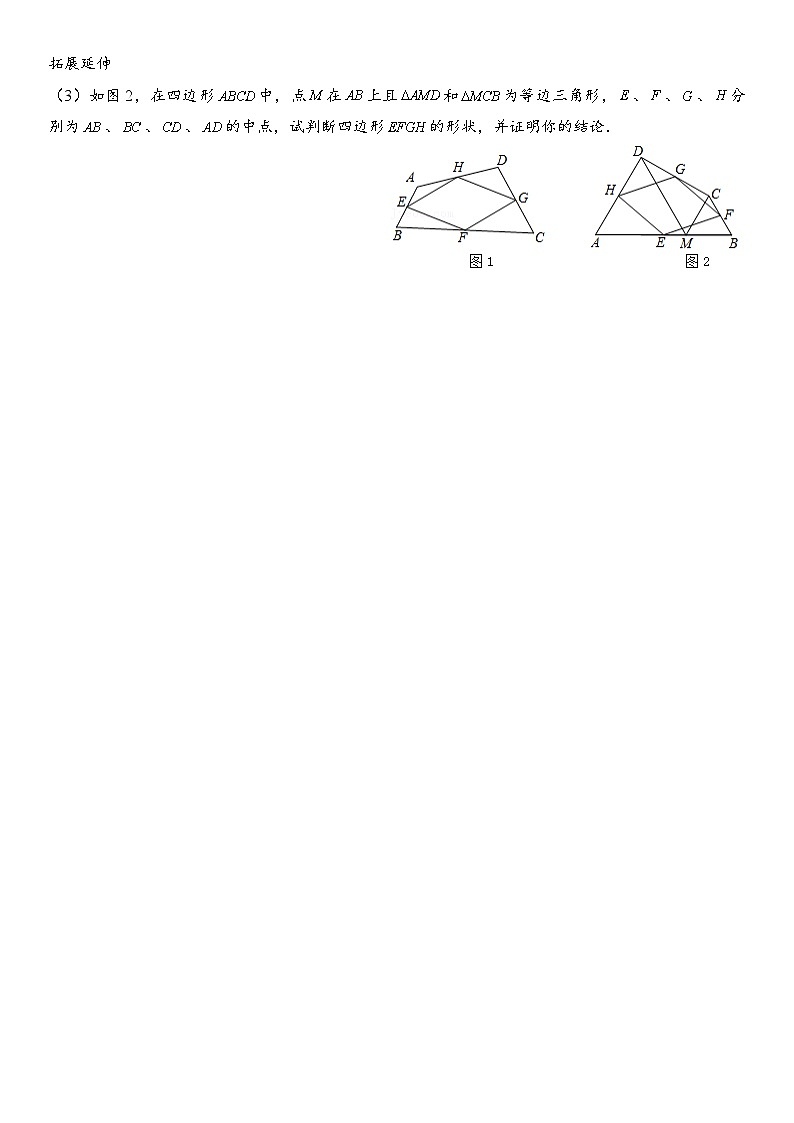
2.(2017春•建湖县期中)阅读理解我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形.如图1,在四边形中,,,,分别是边,,,的中点,依次连接各边中点得到中点四边形.
问题解决
(1)判断图1中的中点四边形的形状,并说明理由;
(2)当图1中的四边形的对角线添加条件 时,这个中点四边形是正方形.
拓展延伸
(3)如图2,在四边形中,点在上且和为等边三角形,、、、分别为、、、的中点,试判断四边形的形状,并证明你的结论.
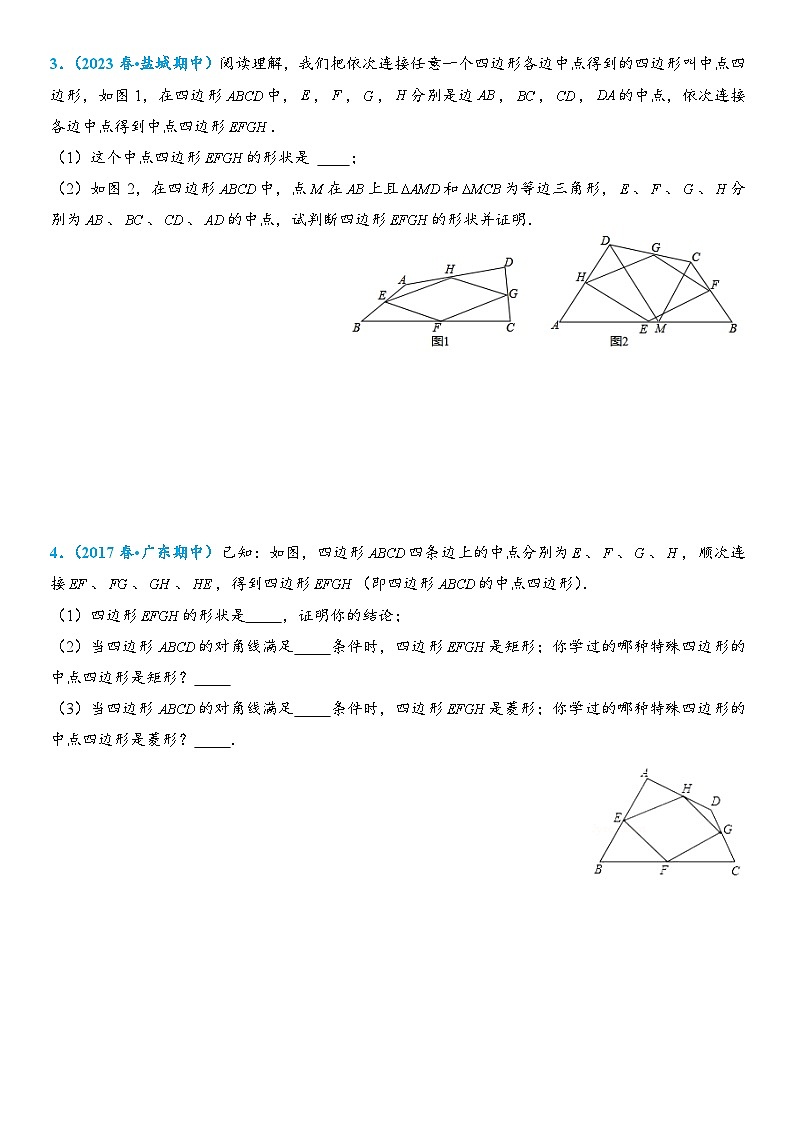
3.(2023春•盐城期中)阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形中,,,,分别是边,,,的中点,依次连接各边中点得到中点四边形.
(1)这个中点四边形的形状是 ;
(2)如图2,在四边形中,点在上且和为等边三角形,、、、分别为、、、的中点,试判断四边形的形状并证明.
4.(2017春•广东期中)已知:如图,四边形四条边上的中点分别为、、、,顺次连接、、、,得到四边形(即四边形的中点四边形).
(1)四边形的形状是 ,证明你的结论;
(2)当四边形的对角线满足 条件时,四边形是矩形;你学过的哪种特殊四边形的中点四边形是矩形?
(3)当四边形的对角线满足 条件时,四边形是菱形;你学过的哪种特殊四边形的中点四边形是菱形? .
5.(2015春•饶平县期末)我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,、、、分别是四边形各边的中点,可证中点四边形是平行四边形,如果我们对四边形的对角线与添加一定的条件,则可使中点四边形成为特殊的平行四边形,请你经过探究后回答下面问题?
(1)①当 时,四边形为菱形;
②当 时,四边形为矩形.
(2)当和满足什么条件时,四边形为正方形?请回答并证明你的结论.
6.(2014•龙岩)如图,我们把依次连接任意四边形各边中点所得四边形叫中点四边形.
(1)若四边形是菱形,则它的中点四边形一定是 ;
.菱形 .矩形 .正方形 .梯形
(2)若四边形的面积为,中点四边形的面积记为,则与的数量关系是 ;
(3)在四边形中,沿中点四边形的其中三边剪开,可得三个小三角形,将这三个小三角形与原图中未剪开的小三角形拼接成一个平行四边形,请画出一种拼接示意图,并写出对应全等的三角形.
7.(2023•乐清市模拟)如图,是的对角线的交点,,,分别是,,的中点.
(1)求证:四边形是平行四边形.
(2)当,,时,求四边形的周长.
8.(2023春•姜堰区期中)如图,在四边形中,点、、、分别是、、、的中点,连接、.
(1)求证:四边形是平行四边形;
(2)当对角线与满足什么关系时,四边形是菱形,并说明理由.
9.(2022春•工业园区校级期末)如图,四边形中,点、、、分别为、、、的中点,
(1)求证:中点四边形是平行四边形;
(2)如图2,点是四边形内一点,且满足,,,点、、、分别为、、、的中点,猜想中点四边形的形状,并证明你的猜想.
10.(2019秋•金水区校级月考)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图,点是四边形内一点,且满足,,,点,,,分别为边,,,的中点,猜想中点四边形的形状,并证明你的猜想;
(2)若改变(1)中的条件,使,其他条件不变,直接写出中点四边形的形状(不必证明).
2024年中考数学压轴题专项练习—四边形中的对角互补模型: 这是一份2024年中考数学压轴题专项练习—四边形中的对角互补模型,文件包含52四边形中的对角互补模型答案docx、52四边形中的对角互补模型docx等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。
2024年中考数学压轴题专项练习—风筝模型: 这是一份2024年中考数学压轴题专项练习—风筝模型,文件包含39风筝模型答案docx、39风筝模型docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
2024年中考数学压轴题专项练习—垂美四边形模型: 这是一份2024年中考数学压轴题专项练习—垂美四边形模型,文件包含49垂美四边形模型答案docx、49垂美四边形模型docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。












