



2024年中考数学压轴题专项练习—转化思想
展开1、以专题复习为主。如选择题、填空题的专项练习,要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习,深化对常考题型的熟悉程度。在函数复习过程中,如果考生未能完全理解简单实例中的数量关系和变化规律,针对此类问题,在专项复习中,可以通过选择题、填空题的专项练习,进行突破,如“读懂图象信息问题”等,将复杂问题由浅入深,层层分解,提高分析和判断能力。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法,要通过典型试题的训练,进一步渗透和深刻理解其内涵,重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度,培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来,通过一题多解,积极地探求解决问题的最优解法,这样,对于解决难度较大的压轴题会有很大的帮助。
转化思想
1.(2022秋•扶风县期末)二次函数的部分图象如图所示,其中图象与轴交于点,与轴交于点,且经过点.
(1)求此二次函数的解析式;
(2)将此二次函数的解析式写成的形式,并直接写出顶点坐标以及它与轴的另一个交点的坐标.
(3)利用以上信息解答下列问题:若关于的一元二次方程为实数)在的范围内有解,则的取值范围是 .
【解答】解:(1)根据题意得,
,
②分别代入①、③得,
④,
⑤,
④⑤得,,
解得,
把代入④得,,
解得,
方程组的解是
,
此二次函数的解析式为;
(2),
二次函数的解析式为,
顶点坐标为,
对称轴为,
设另一点坐标为,
则,
解得,
点的坐标是;
(3)由(1)可知二次函数解析式为,
即,
时,,
时,,
关于的一元二次方程为实数)在的范围内有解相当于与直线的交点的横坐标,
当时,在的范围内有解.
故答案为:.
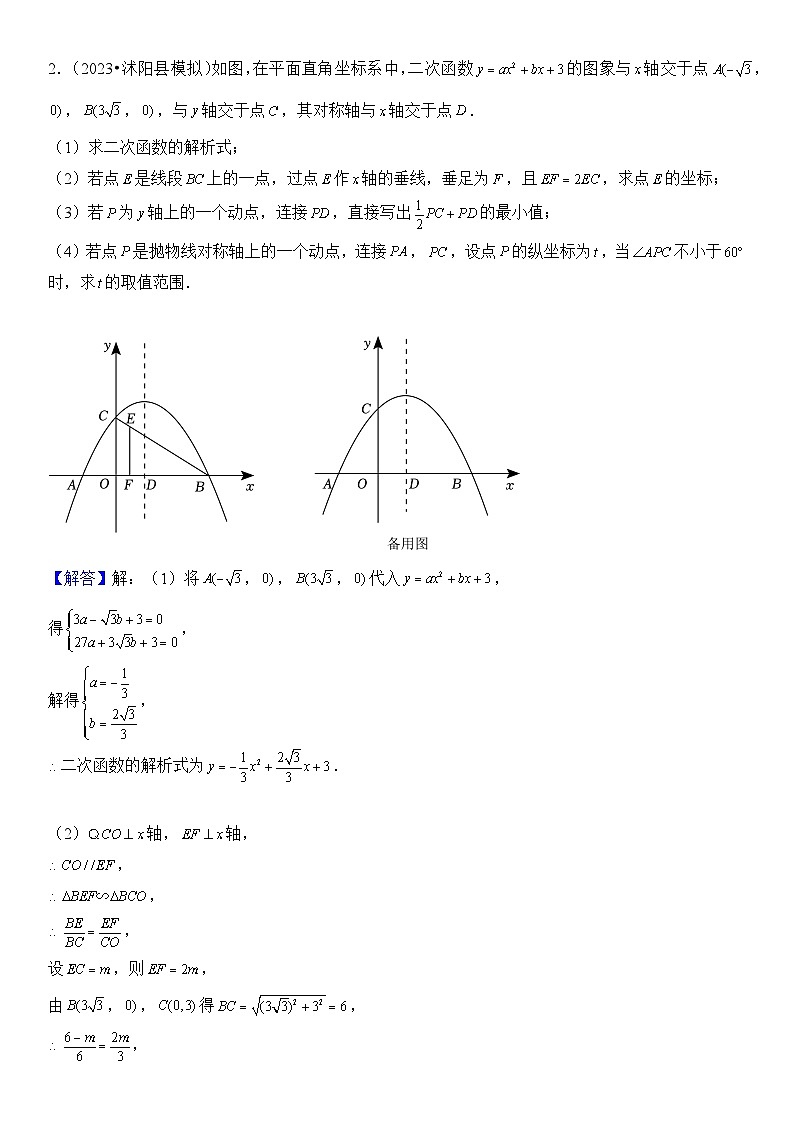
2.(2023•沭阳县模拟)如图,在平面直角坐标系中,二次函数的图象与轴交于点,,,,与轴交于点,其对称轴与轴交于点.
(1)求二次函数的解析式;
(2)若点是线段上的一点,过点作轴的垂线,垂足为,且,求点的坐标;
(3)若为轴上的一个动点,连接,直接写出的最小值;
(4)若点是抛物线对称轴上的一个动点,连接,,设点的纵坐标为,当不小于时,求的取值范围.
【解答】解:(1)将,,,代入,
得,
解得,
二次函数的解析式为.
(2)轴,轴,
,
,
,
设,则,
由,,得,
,
解得:,
,
又由得,
,
,;
(3)过点作直线直线,
再,直线,
则四边形是矩形,
,
,
,
,
当,,三点共线时,的值最小,
此时,直线,
又作则,
直线,直线,直线,
四边形是矩形,
,
,
的值最小值为3.
(4),,
则,
,
作的平分线,交轴于,
则,
,
以为圆心,为半径作圆,与抛物线对称轴交于点,,
当点在圆上时,则,
当点在圆内时,,
当点在圆外时,,
过作垂直于对称轴,
在中,,,则,
在△中,,
,,
.
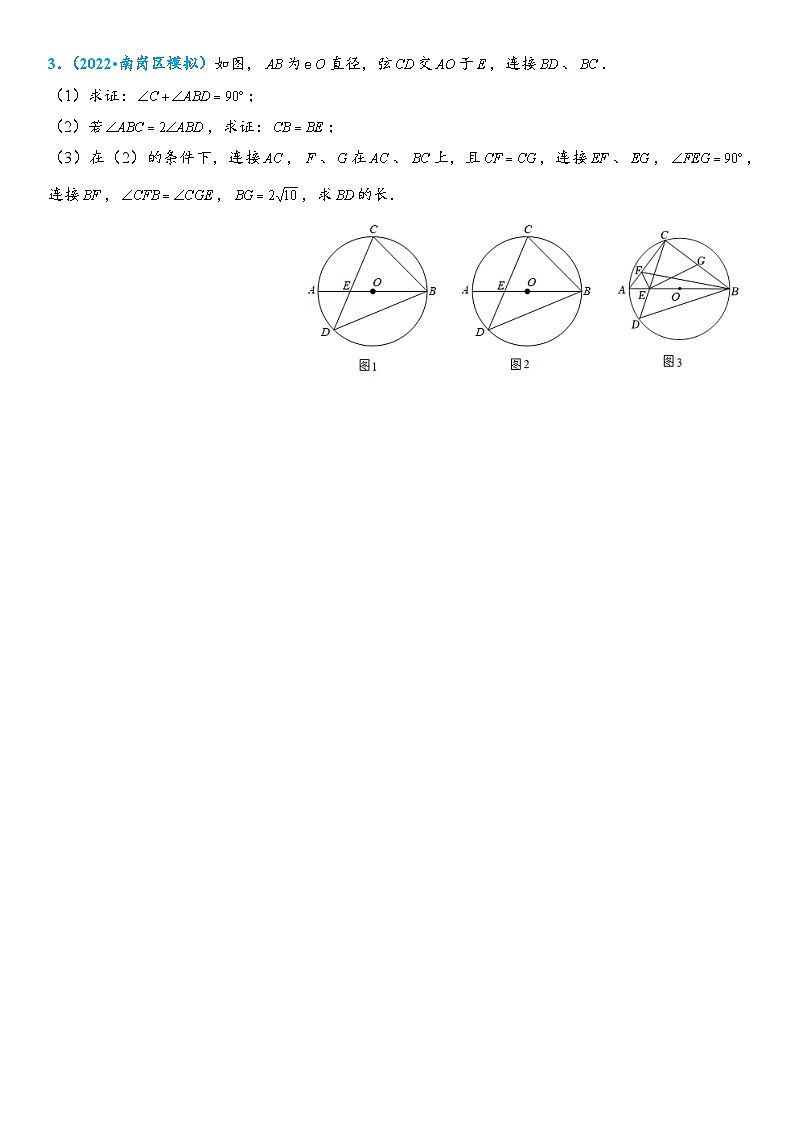
3.(2022•南岗区模拟)如图,为直径,弦交于,连接、.
(1)求证:;
(2)若,求证:;
(3)在(2)的条件下,连接,、在、上,且,连接、,,连接,,,求的长.
【解答】证明:(1)如图1,连接,
,
,
是直径,
,
,
.
(2),设,
,
,
,
,
,
,
.
(3)如图2,延长,使,连接,延长、交于点,
,,
四边形对角互补且邻边相等,
,
在中,,,
设,则
,
,
,
,
,
,
,
再设,则
,
,
,
,,
,
,,
,
,
,
,
点为中点,点为中点,
再设,则
,
,
,
,
,
,
,
,
,
再设,则
在中,有
,
解得,
,
,,
,
在中,如图3,过点作于点,
设,则
,,,,
,
,
.
4.(2021•罗平县模拟)如图,是的直径,是弦,点在圆外,于点,交于点,连接、、,.
(1)求证:是的切线;
(2)求证:;
(3)设的面积为,的面积为,若,求的值.
【解答】解:(1)证明:,
又,
,
于点,
,
,
,即,
,
是的切线;
(2),,
,
,
,
,
;
(3)为直径,
,
,
,
,
,
在中,,
设,则,
,
于点,
,
,
由(2)知,
,
而,
,
,
设,则,
的面积为,
而的面积为,
.
5.(2021•商河县校级模拟)(1)初步思考:
如图1,在中,已知,,为上一点且,试证明:
(2)问题提出:
如图2,已知正方形的边长为4,圆的半径为2,点是圆上的一个动点,求的最小值.
(3)推广运用:
如图3,已知菱形的边长为4,,圆的半径为2,点是圆上的一个动点,求的最大值.
【解答】(1)证明:如图1,
,,,
,.
.
.
又,
.
.
;
(2)如图2,在上取一点,使得,
(3)同(2)中证法,如图3,
当点在的延长线上时,的最大值,最大值为.
6.(2020•长安区校级模拟)如图所示,二次函数的图象与轴交于点、,与轴交于点,点的坐标为,是抛物线上一点(点与点、、不重合)
(1)则系数 ;点的坐标是 ;
(2)设直线与直线相交于点,是否存在这样的点,使得?若存在,求出点的横坐标;若不存在,请说明理由;
(3)连接、,判断和的数量关系,并说明理由;
(4)设点在二次函数的图象上,以点为圆心,半径为的圆与直线相切,求点的坐标.
【解答】解:(1)把点代入,
得,
,
抛物线的解析式为.
当时,有,
解得,,
点的坐标为,,
故答案为:;,.
(2)(方法一)在中,
令,得,
.
设直线的解析式为,
把、代入中,
得,
解得,
直线的解析式为.
假设存在,设点的坐标为.
①当点、在直线的异侧时,
作轴,轴,
,
,
,
,
,,
,,,,
,,
,,
,,
点的坐标为,,
点在抛物线上,
把点代入得,
整理,得,
△,
方程无解,即不存在符合题意得点,(舍去);
②当点、在直线的同侧时,
同理得,点的坐标为,,
点在抛物线上,
把点代入得,
整理,得,
解得,,
点的横坐标为或,
综上所述:存在点,使得,点的横坐标为或.
(3)(解法一),理由如下:
作的角平分线,交轴于点,过点作于点,
点,,点,
,,.
设,则,,
由面积法,可知:,即,
解得:.
,,
,
,
.
(解法二),理由如下:
将沿轴对折,交轴于点,
点,,点,点,
点,,
,,
,
,.
,
.
(4)以点为圆心,半径为的圆与直线相切,
点到直线的距离为,
直线的解析式为,即,
过点作的平行线,
则直线与直线的距离为,
设直线解析式为,即,
根据两条平行线之间的距离公式(补充),
若直线为:,直线为:,
则直线与直线的距离是:,
由直线与直线的解析式得,
,
或,
当时,直线为,
联立,
消整理得,
此方程无解,(舍去),
当时,直线为,
联立,
消整理得,
,,
点的坐标为,.
7.(2018•雁塔区校级模拟)问题提出
(1)如图1,正方形的对角线交于点,是边长为6的等边三角形,则、之间的距离为 ;
问题探究
(2)如图2,在边长为6的正方形中,以为直径作半圆,点为弧上一动点,求、之间的最大距离;
问题解决
(3)窑洞是我省陕北农村的主要建筑,窑洞宾馆更是一道靓丽的风景线,是因为窑洞除了它的坚固性及特有的外在美之外,还具有冬暖夏凉的天然优点家住延安农村的一对即将参加中考的双胞胎小宝和小贝两兄弟,发现自家的窑洞(如图3所示)的门窗是由矩形及弓形组成,,,弓高为的中点,,小宝说,门角到门窗弓形弧的最大距离是、之间的距离.小贝说这不是最大的距离,你认为谁的说法正确?请通过计算求出门角到门窗弓形弧的最大距离.
【解答】解:(1)如图1,连接,,对角线交点为,连接交于,
则,
为等边三角形,
,
垂直平分,
,
四边形为正方形,
为等腰直角三角形,
,
在中,
,
,
故答案为:;
(2)如图2,补全,连接并延长交右半侧于点,则此时、之间的距离最大,
在中,,,
,
;
(3)小贝的说法正确,理由如下,
如图3,补全弓形弧所在的,连接,,过点作于点,连接并延长交上端于点,
则此时、之间的距离即为门角到门窗弓形弧的最大距离,
由题意知,点为的中点,
,,
在中,
设,则,
,
,
解得,,
,
在中,,,
,
,
门角到门窗弓形弧的最大距离为.
8.(2023•宝安区校级三模)如图①,已知线段与直线,过、两点,作使其与直线相切,切点为,易证,可知点对线段的视角最大.
问题提出
(1)如图②,已知的外接圆为,与相切于点,交的延长线于点.
①请判断与的大小关系,并说明理由.
②若,,求的长.
问题解决
(2)如图③,一大型游乐场入口设在道路边上,在“雪亮工程”中,为了加强安全管理,结合现实情况,相关部门准备在与地面道路夹角为的射线方向上(位于垂直于地面的平面内)确定一个位置,并架设斜杆,在斜杆的中点处安装一摄像头,对入口实施监控(其中点、、、、、、在同一平面内),已知米,米,调研发现,当最大时监控效果最好,请问在射线上是否存在一点,使得达到最大?若存在,请确定点在上的位置及斜杆的长度;若不存在,请说明理由.
【解答】(1)解:①,理由如下:
如图②,连接并延长至圆上一点,连接,
则,
为圆的直径,
,
,
与相切于点,
,
,
,
,
.
②,,
,
,
,,
,
,
.
(2)解:存在一点,使得达到最大.
如图③,取的中点,过点作的平行线,
经过,作与相切于点,
由题意知,此时最大.
,是中点,
,,
作直径,连接,
则,,
,
是的切线,是切点,
,
,
,
又,
,
,
,
.
过点作于,
,
,
,
,
,
由勾股定理得,
,
.
故点在上距离点处,斜杆的长度为.
9.(2023•永兴县二模)如图1,抛物线与轴相交于原点和点,直线与抛物线在第一象限的交点为点,抛物线的顶点为点.
(1)求点和点的坐标;
(2)抛物线上是否存在点,使得?若存在,求出所有点的坐标;若不存在,请说明理由;
(3)如图2,点是点关于抛物线对称轴的对称点,点是直线下方的抛物线上的动点,与直线交于点.设和的面积分别为和,求的最大值.
【解答】解:(1)抛物线,
,
当时,有最小值,
.
直线与抛物线在第一象限的交点为点,
联立,
解得或(舍去),
.
故点和点的坐标分别为和;
(2)设直线的解析式为:,
则将,代入得,
,
解得,
直线的解析式为:.
①当点在直线的下方时,过点作轴,交轴于点,延长,交于,
,
,即,,
,
,
,
.
当时,,得:,
,
则,
,
易知直线的解析式为:,
联立:,
解得或(舍去),
;
②当点在直线的上方时,
,
,
直线的解析式为:,
直线的解析式为:,
联立:,解得:或(舍去),
.
综上,当点的坐标为或时,使得;
(3)点与点关于对称轴对称,
,
如图,分别过点,作轴的平行线,交直线于点,,
,,
设,则,
,
,,
,
当时,的最大值为.
10.(2022•瑶海区三模)已知抛物线;
(1)若抛物线的顶点坐标为,求、的值;
(2)当,时,抛物线的最小值是,求的值;
(3)当,时,恒成立,则的最大值为 4 .
【解答】解:(1)抛物线的顶点坐标为,
,
,,;
(2)
,对称轴为,
①当时,由题意可知,解得,符合题意;
②当时,,解得,,不合题意舍去;
③当时,根据题意可知,解得,符合题意;
综上所述,所求的值为或.
(3)当时,抛物线的解析式为,
如图所示,抛物线的顶点在直线上移动,
当时,恒成立,
则可知抛物线的顶点坐标为,
设抛物线与直线除顶点外的另一个交点为,
此时点的横坐标即为的最大值,
由解得,,
的最大值为4.
11.已知如图,直线的图象与轴,轴分别相交于、两点,点在线段上由向点以每秒2个单位运动,点在线段上由向点以每秒1个单位运动(其中一点先到达终点则都停止运动),设运动的时间为秒.
(1)请直接写出,两点的坐标;
(2)当值为多少时,为等边三角形?
(3)是否存在的值,使为直角三角形?若存在,求出的值:若不存在,说明理由.
【解答】解:(1)令,则,解得:,
;
令,则,
;
(2)在中,
,,
,
,,
,
,
,
当时,为等边三角形,
即,解得,
当时,为等边三角形;
(3)存在,理由:
,,
①当,
由(2)知,
,
,
即,解得;
②当,
由(2)知,
,
,
即,解得,
当或时,为直角三角形.
12.(2022•雁塔区校级四模)(1)如图①,在中,,,,求外接圆的半径;
(2)如图②,是一个半径为200米的圆形广场,弦是广场上一个长为米的纳凉演绎舞台,现计划在广场上建一个长为200米的手工艺集市,并在舞台和集市之间修建两个休闲长廊和,规划长廊、舞台、集市围成四边形为活动区域,那么能否在优弧上确定两点、,使得长廊最长?若能,请求出的最大值,并计算此时的度数及四边形的面积;若不能,请说明理由.
【解答】解:(1)设外接圆为,连接,,交于点,如图,
,
,
,,
,,
,
为等边三角形.
,
在中,
,
;
(2)在优弧上确定两点、,使得长廊最长.
连接,,,,过点分别作,,,垂足分别为,,,如图,
的半径为200米,米,
米,
,
,
.
米,
为等边三角形,
,
.
.
,,
.
,
,
.
在和中,
,
.
.
,,
,,
.
,
,
,
.
,
当最大时,取最大值,
,
当,,最大,即最大,最大值为20000,
当时,的值最大.
在优弧上确定两点、,使得长廊最长;
此时,如图,
,,
.
四边形的面积
米.
13.(2021秋•龙湖区校级月考)如图①,的半径为5,点、在上运动,以为边向圆心方向作正方形.
(1)当时,判断并证明点与的位置关系;
(2)如图②,当直线与相切时,求的长;
(3)请直接写出、两点距离的最小值.
【解答】解:(1)点在上.
理由如下:
过点作于,作于,得矩形,如图1,
,
,
,
,
,
,
点在上;
(2)连接、,延长与交于点,过作于,如图2,则,
与相切于点,
,
,
,
,
,
四边形和四边形是矩形,
,,
设,则,
,
,
,
解得,或(舍,
;
(3)、两点距离的最小值为.
理由如下:
如图3,连接,并延长与交于点,连接、、、、,则,
四边形是正方形,
,,,
,
,
,
,
在和中,
,
,
,
,
当、、三点共线时,取最小值为.
故、两点距离的最小值为.
14.(2021•南岸区校级模拟)初中阶段的函数学习中,我们经理了列表、描点、连线画函数图象,并结合图象研究函数性质的过程,以下我们研究函数性质及应用的部分过程,请按要求完成下列各小题.
(1)下表是与的几组值,请在表格中的空白处填上恰当的数字;
(2)在平面直角坐标系中,补全描出表格中数据对应的各点,补全函数图象;
(3)观察函数的图象,请写出函数的一条性质: .
(4)若方程为常数)有三个实数解,则的取值范围为 .
【解答】解:(1)时,;
时,,
故答案为:,2;
(2)图象如图所示:
(3)当时,函数有最小值,没有最大值;
故答案为:当时,函数有最小值,没有最大值;
(4)如图:
由,可知,
令,
当或时,,
,
当△时,,
解得或,
此时函数与有两个交点,
函数与也有两个交点,
当时,,此时函数与有两个交点,
时,函数与有三个交点,
方程为常数)有三个实数解,则的取值范围为,
故答案为:.
15.(2021秋•惠民县月考)小刚在用描点法画抛物线时,列出了下面的表格:
(1)请根据表格中的信息,写出抛物线的一条性质: 抛物线的对称轴是直线(答案不唯一) ;
(2)求抛物线的解析式;
(3)抛物线与轴的交点分别为、在的左侧)与轴的交点为,其对称轴与轴的交点为,在抛物线的对称轴上存在点,使是以为腰的等腰三角形,求出点的坐标;
(4)在(3)的条件下,抛物线上有一点,使的内心在轴上,直接写出点的坐标.
【解答】解:(1)抛物线经过,,
抛物线的对称轴是直线;
故答案为:抛物线的对称轴是直线(答案不唯一);
(2)抛物线经过,,,
,
解得,
抛物线的解析式为;
(3)如图1,
抛物线,
抛物线的对称轴,
,
,
,
在中,由勾股定理得,
是以为腰的等腰三角形,
,
如图所示,作对称轴于,
,
,
,,,,,.
(4)如图2.作点关于轴的对称点,则,连接并延长与抛物线交于点,由图形的对称性可知为所求的点,
设直线的解析式为,
由题意得:,
解得:,
直线的解析式为,
将直线和抛物线的解析式联立得:
,
解得(舍去)或,
.
16.(2021•滨城区一模)如图,在中,,,点在上,以为直径的经过点.
(1)求证:①是的切线;
②;
(2)若点是劣弧的中点,且,试求阴影部分的面积.
【解答】(1)①证明:如图1,
连接,
,
,
(圆周角定理),
,
,
根据题意可知,
,
是的切线.
②如图2,
连接,,
为直径,,
,,
由(1)可知,
,
在和中,
,
,
,
故.
(2)如图3,
连接、、,和交于点,
则,
根据题意点是劣弧的中点,且,
,
和是等边三角形,
,
,
由(1)可知,
,
在和中,
,
,
,
.
17.(2017•商水县一模)自主学习,请阅读下列解题过程.
解一元二次不等式:
解:设,解得,,则抛物线与轴的交点坐标为和.画出二次函数的大致图象(如图所示),由图象可知:当,或时函数图象位于轴上方,此时,即,所以,一元二次不等式的解集为:,或.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)一元二次不等式的解集为 .
(2)用类似的方法解一元二次不等式:.
【解答】解:(1)由例题的图形可得:一元二次不等式的解集为:;
故答案为:;
(2)设,则是的二次函数.
,
抛物线开口向上.
又当时,,
解得:,.
由此得抛物线的大致图象如图所示.
观察函数图象可知:当或时,.
的解集是:或.
18.(2023•忻州模拟)阅读与思考
如图是小强同学的数学课堂笔记本,请仔细阅读,并完成相应的任务.
任务:(1)上面课堂笔记中的分析过程,主要运用的数学思想是 (从下面选项中选出两个即可);
.数形结合
.统计思想
.分类讨论
.转化思想
(2)选择一种课堂笔记本中记载的方法,求出“情况一”中的坐标.
(3)直接写出“情况二”中的坐标 ;
(4)请你写出在“情况三”中,确定、的坐标位置及求坐标过程中,所依据的数学定理或原理(写出一个即可).
【解答】解:(1)上面课堂笔记中的分析过程,主要运用的数学思想是数形结合和转化思想.
故选:.
(2)当为直角顶点时,过点作的垂线交直线于点,
,
,
又,
,
△,
,,,,
,解得,
的坐标为.
(3)过作轴交轴于点,如图:
则,
当为直角顶点时,过点作的垂线交直线于点,
,
,
.
,
△,
,,,,
,解得,
的坐标为.
(3)当为直角顶点时,以为直径作圆,则该圆与直线的交点即为所求点.
,,
与(2)同理可得△△,△△,
,,
设的坐标为,的坐标为,
则,,,;,,,,
,,
解得,或(舍去),
的坐标为,的坐标为,
在求解过程中依据的定理是相似三角形的对应边成比例.
19.(2023•庐阳区校级三模)直线y1=x+b经过点A(1,0),抛物线经过点B(2,m),其中a和b为实数.设抛物线y2=x2﹣2ax+4a﹣6的顶点为M,过M作y轴的平行线交直线y1=x+b于点N.
(1)求b和m的值;
(2)当抛物线顶点M的纵坐标取得最大值时,求线段MN的值;
(3)求线段MN的最小值.
【解答】解:(1)把点A代入y1得1+b=0,解得b=﹣1.
把点B代入y2得m=﹣2.
∴b=﹣1,m=﹣2.
(2)M是y2的顶点,利用顶点公式可得M的坐标为(a,﹣a2+4a﹣6),
当a=2时,纵坐标有最大值是﹣10,
此时M的坐标为(2,﹣2),N的坐标为(2,1),
∴MN=1﹣(﹣2)=3.
(3)点M的坐标为(a,﹣a2+4a﹣6),点N的坐标为(a,a﹣1),
∴MN=a﹣1﹣(﹣a2+4a﹣6)=a2﹣3a+5=(a﹣)2+,
∴当a=时,MN有最小值是.
20.(2023•微山县二模)如图,中,,的平分线交于点,点在上,以点为圆心,以为半径的圆经过点,交于点,交于点.
(1)求证:与相切;
(2)若,,求的长.
【解答】(1)证明:连接,
是半径
,
,
的平分线交于点,
,
,
,
,
是的切线;
(2)解:连接,
,
,
,
为直径,
,
,
,
,
,
,
,
,
,
,即:,
解得:.
0
1
3
4
5
0
4
0
1
2
3
4
0
2
3
3
2
0
平面直角坐标系与直角三角形
年月日星期三
原理:根据直角三角形的定义,性质,判定,以直角三角形顶点分三种情况进行分类讨论.口诀:“两线一圆”
作图:举例如下:已知、,在直线上求点,使得为直角三角形.以下分三种情况讨论:
情况一:当为直角顶点时,过点作的垂线交直线于点,则交点即为所求点.如图①,有一个点;
情况二:当为直角顶点时,过点作的垂线交直线于点,则交点即为所求点.如图②,有一个点;
情况三:当为直角顶点时,以为直径作圆,则该圆与直线的交点即为所求点.如图③,有,两个点;
方法:一、几何法:构造“型”或“一线三垂直”相似;
二、代数法:两点间的距离公式,列方程,解方程,检验根;
三、解析法:求垂线解析式,联立方程组求交点.
2024年中考数学压轴题专项练习—整体思想: 这是一份2024年中考数学压轴题专项练习—整体思想,文件包含80整体思想答案docx、80整体思想docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
2024年中考数学压轴题专项练习—数学建模思想: 这是一份2024年中考数学压轴题专项练习—数学建模思想,文件包含81数学建模思想答案docx、81数学建模思想docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
2024年中考数学压轴题专项练习—数形结合思想: 这是一份2024年中考数学压轴题专项练习—数形结合思想,文件包含78数形结合思想答案docx、78数形结合思想docx等2份试卷配套教学资源,其中试卷共67页, 欢迎下载使用。












