

中考数学几何模型专项复习 模型29 平行四边形——中点四边形模型-(原卷版+解析)
展开中点四边形:依次连接四边形四边中点连线的四边形得到中点四边形.
◎结论1:点M、N、P、Q是任意四边形的中点,则四边形MNPQ是平行四边形.
如上图:
【证明】
∵MN∥12BD
PQ∥12BD
∴四边形MNPQ为平行四边形。
如上图
【证明】
∵MQ∥12BD,MQ=12BD
PN∥12BD,PN=12BD
∴MQ∥PN,MQ=PN
∴四边形MNPQ为平行四边形
【证明】
∵MN∥12AC,MN=12AC
PQ∥12AC,PQ=12AC
∴MN∥PQ,MN=PQ
∴四边形MNPQ为平行四边形
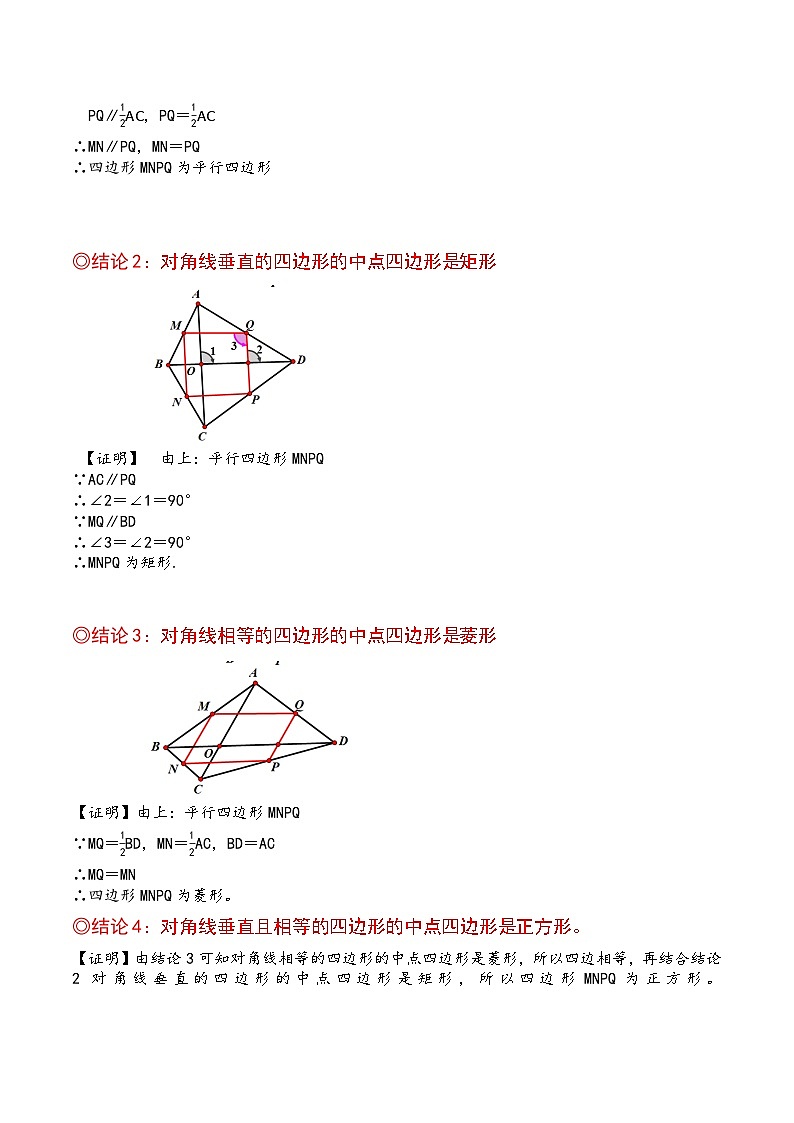
◎结论2:对角线垂直的四边形的中点四边形是矩形
【证明】 由上:平行四边形MNPQ
∵AC∥PQ
∴∠2=∠1=90°
∵MQ∥BD
∴∠3=∠2=90°
∴MNPQ为矩形.
◎结论3:对角线相等的四边形的中点四边形是菱形
【证明】由上:平行四边形MNPQ
∵MQ=12BD,MN=12AC,BD=AC
∴MQ=MN
∴四边形MNPQ为菱形。
◎结论4:对角线垂直且相等的四边形的中点四边形是正方形。
【证明】由结论3可知对角线相等的四边形的中点四边形是菱形,所以四边相等,再结合结论2 对角线垂直的四边形的中点四边形是矩形,所以四边形MNPQ为正方形。
1.(2023·贵州·遵义五十七中八年级期中)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是
A.任意一个四边形的中点四边形是菱形
B.任意一个平行四边形的中点四边形是平行四边形
C.对角线相等的四边形的中点四边形是矩形
D.对角线垂直的四边形的中点四边形是正方形
2.(2023·山东·淄博市临淄区皇城镇第一中学九年级期中)若顺次连接一个四边形的四边中点所组成的四边形是矩形,则原四边形一定是( )
A.一般平行四边形B.对角线互相垂直的四边形C.对角线相等的四边形D.矩形
3.(2023·新疆农业大学附属中学八年级期中)如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加一个条件 _____,能使四边形EFGH是矩形.
1.(2023·广西桂林·八年级期末)如图,四边形ABCD的四边中点分别为E、F、G、H,顺次连接E、F、G、H.
(1)判断四边形EFGH形状,并说明理由;
(2)若AC=BD,判断四边形EFGH形状,并说明理由.
2.(2023·河北石家庄·八年级期中)四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四边形EFGH称为中点四边形.
(1)我们知道:无论四边形ABCD怎样变化,它的中点四边形EFGH都是平行四边形.特殊的:
①当对角线时,四边形ABCD的中点四边形为__________形;
②当对角线时,四边形ABCD的中点四边形是__________形.
(2)如图:四边形ABCD中,已知,且,请利用(1)中的结论,判断四边形ABCD的中点四边形EFGH的形状并进行证明.
3.(2023·江苏·高港实验学校八年级阶段练习)如图1,在四边形中,如果对角线和相交并且相等,那么我们把这样的四边形称为等角线四边形.
(1)①在“平行四边形、矩形、菱形”中,______一定是等角线四边形(填写图形名称);
②若、、、分别是等角线四边形四边、、、的中点,当对角线、还要满足______时,四边形是正方形.
(2)如图2,已知在中,,,,为平面内一点.
①若四边形是等角线四边形,且,求符合条件的等角线四边形的面积.
②设点是所在平面上的任意一点且,若四边形是等角线四边形,求出四边形面积的最大值,并说明理由.
1.我们给出如下定义:顺次连接任意一个四边形各边中所得的四边形叫中点四边形.
(1)如图1,在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,中点四边形EFGH是 .
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点.猜想中点四边形EFGH的形状,并证明你的猜想.
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).
平行四边形
模型(二十九)——中点四边形模型
中点四边形:依次连接四边形四边中点连线的四边形得到中点四边形.
◎结论1:点M、N、P、Q是任意四边形的中点,则四边形MNPQ是平行四边形.
如上图:
【证明】
∵MN∥12BD
PQ∥12BD
∴四边形MNPQ为平行四边形。
如上图
【证明】
∵MQ∥12BD,MQ=12BD
PN∥12BD,PN=12BD
∴MQ∥PN,MQ=PN
∴四边形MNPQ为平行四边形
【证明】
∵MN∥12AC,MN=12AC
PQ∥12AC,PQ=12AC
∴MN∥PQ,MN=PQ
∴四边形MNPQ为平行四边形
◎结论2:对角线垂直的四边形的中点四边形是矩形
【证明】 由上:平行四边形MNPQ
∵AC∥PQ
∴∠2=∠1=90°
∵MQ∥BD
∴∠3=∠2=90°
∴MNPQ为矩形.
◎结论3:对角线相等的四边形的中点四边形是菱形
【证明】由上:平行四边形MNPQ
∵MQ=12BD,MN=12AC,BD=AC
∴MQ=MN
∴四边形MNPQ为菱形。
◎结论4:对角线垂直且相等的四边形的中点四边形是正方形。
【证明】由结论3可知对角线相等的四边形的中点四边形是菱形,所以四边相等,再结合结论2 对角线垂直的四边形的中点四边形是矩形,所以四边形MNPQ为正方形。
1.(2023·贵州·遵义五十七中八年级期中)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是
A.任意一个四边形的中点四边形是菱形
B.任意一个平行四边形的中点四边形是平行四边形
C.对角线相等的四边形的中点四边形是矩形
D.对角线垂直的四边形的中点四边形是正方形
答案:B
分析中点四边形的形状取决于原四边形的对角线的性质:当原四边形的对角线既不相等,也不垂直时,中点四边形的形状为平行四边形;当原四边形的对角线相等时,中点四边形的形状为菱形;当原四边形的对角线垂直时,中点四边形的形状为矩形;当原四边形的对角线互相垂直且相等时,中点四边形的形状为正方形.由此即可解答.
【详解】选项A,由任意一个四边形的中点四边形是平行四边形可判定选项A错误;
选项B,任意一个平行四边形的中点四边形是平行四边形,选项B正确;
选项C,由对角线相等的四边形的中点四边形是菱形可判定选项C错误;
选项D,由对角线垂直的四边形的中点四边形是矩形可判定选项D错误.
故选B.
【点睛】本题考查了中点四边形的性质,熟知中点四边形的形状取决于原四边形的对角线的性质是解决问题的关键.
2.(2023·山东·淄博市临淄区皇城镇第一中学九年级期中)若顺次连接一个四边形的四边中点所组成的四边形是矩形,则原四边形一定是( )
A.一般平行四边形B.对角线互相垂直的四边形C.对角线相等的四边形D.矩形
答案:B
【详解】因为任意四边形的中点四边形都是平行四边形,而中点四边形的两组对边分别是和原四边形的两条对角线平行的,矩形相邻两边是互相垂直的,所以原四边形的对角线应该互相垂直.
故选B.
3.(2023·新疆农业大学附属中学八年级期中)如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加一个条件 _____,能使四边形EFGH是矩形.
答案:AC⊥BD
分析根据三角形的中位线平行于第三边,根据平行线的性质可得:∠EHG=∠1,∠1=∠2,再证明四边形EFGH是平行四边形,当∠EFG=90°,四边形EFGH是矩形,所以∠2=90°,因此AC⊥BD.
【详解】解:如图,
∵G、H、E分别是BC、CD、AD的中点,
∴
∴∠EHG=∠1,∠1=∠2,
∴∠2=∠EHG,
同理:
∴四边形EFGH是平行四边形,
当∠EHG=90°, 四边形EFGH是矩形,
∴∠2=90°,
∴AC⊥BD.
故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
【点睛】本题主要考查三角形的中位线定理和矩形的四个角都是直角的性质,熟练掌握定理和性质是解题的关键.
1.(2023·广西桂林·八年级期末)如图,四边形ABCD的四边中点分别为E、F、G、H,顺次连接E、F、G、H.
(1)判断四边形EFGH形状,并说明理由;
(2)若AC=BD,判断四边形EFGH形状,并说明理由.
答案:(1)平行四边形,理由见解析;(2)菱形,理由见解析
分析(1)连接AC,根据三角形中位线定理即可证得;
(2)连接BD ,由(1)得,四边形EFGH是平行四边形,再由三角形中位线定理,证得邻边相等,即可证得菱形.
【详解】(1)四边形EFGH为平行四边形,理由如下:
连接AC,如图,
在△ABC和△ADC中,
∵EF、GH分别为其中位线,
∴EF∥AC,且EF=AC; GH∥AC且GH=AC ,
∴EF=GH,EF∥GH,
∴四边形EFGH为平行四边形;
(2)若AC=BD, 则四边形EFGH为菱形,
连接BD ,如图,
在△BCD中,
∵GF为其中位线,
∴GF=BD ,
∵EF=AC(已证),且AC=BD,
∴EF=GF ,
又∵四边形EFGH为平行四边形(已证),
∴四边形EFGH为菱形.
【点睛】本题主要考查三角形中位线定理,平行四边形的判定,菱形的判定,解题关键是熟练掌握三角形中位线定理.连接三角形两边中点的线段,平行且等于第三边的一半.
2.(2023·河北石家庄·八年级期中)四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四边形EFGH称为中点四边形.
(1)我们知道:无论四边形ABCD怎样变化,它的中点四边形EFGH都是平行四边形.特殊的:
①当对角线时,四边形ABCD的中点四边形为__________形;
②当对角线时,四边形ABCD的中点四边形是__________形.
(2)如图:四边形ABCD中,已知,且,请利用(1)中的结论,判断四边形ABCD的中点四边形EFGH的形状并进行证明.
答案:(1)①菱;②矩;(2)菱形,菱形见解析
分析(1)①连接AC、BD,根据三角形中位线定理证明四边形EFGH都是平行四边形,根据邻边相等的平行四边形是菱形证明;
②根据有一个角是直角的平行四边形是矩形证明;
(2)分别延长BA、CD相交于点M,连接AC、BD,证明,得到AC=DB,根据(1)①证明即可.
【详解】(1)解:(1)①连接AC、BD,
∵点E、F、G、H分别为AB、BC、CD、DA边的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,
同理EF∥HG,
∴四边形EFGH都是平行四边形,
∵对角线AC=BD,
∴EH=EF,
∴四边形ABCD的中点四边形是菱形;
②当对角线AC⊥BD时,EF⊥EH,
∴四边形ABCD的中点四边形是矩形;
故答案为:菱;矩;
(2)四边形ABCD的中点四边形EFGH是菱形.理由如下:
分别延长BA、CD相交于点M,连接AC、BD,
∵,∴是等边三角形,∴,,
∵,∴,∴,,
在和中,
,
∴,∴,
∴四边形ABCD的对角线相等,中点四边形EFGH是菱形.
【点睛】本题考查的是矩形、菱形的判定、中点四边形的定义,掌握中点四边形的概念、矩形的判定定理、菱形的判定定理是解题的关键.
3.(2023·江苏·高港实验学校八年级阶段练习)如图1,在四边形中,如果对角线和相交并且相等,那么我们把这样的四边形称为等角线四边形.
(1)①在“平行四边形、矩形、菱形”中,______一定是等角线四边形(填写图形名称);
②若、、、分别是等角线四边形四边、、、的中点,当对角线、还要满足______时,四边形是正方形.
(2)如图2,已知在中,,,,为平面内一点.
①若四边形是等角线四边形,且,求符合条件的等角线四边形的面积.
②设点是所在平面上的任意一点且,若四边形是等角线四边形,求出四边形面积的最大值,并说明理由.
答案:(1)①矩形;②;(2)①;②18,理由见解析
分析(1)①在“平行四边形、矩形、菱形”中,只有矩形的对角线相等,所以矩形是等角线四边形;②当时,四边形是正方形,首先证明四边形是菱形,再证明有一个角是直角即可;
(2)①如图2中,作于.根据计算,求出相关线段即可;②如图3中,设与相交于点,连接,只要证明当且、、共线时,四边形的面积最大即可.
【详解】解:(1)①在“平行四边形、矩形、菱形”中,
矩形的对角线相等,
矩形一定是等角线四边形,
故答案为:矩形;
②当时,四边形是正方形.
理由:如图1,
、、、分别是等角线四边形四边、、、的中点,
,,,,
,
,
四边形是菱形,
,,,
,
四边形是正方形.
故答案为:;
(2)①如图2,作于.
在中,,,,
,
,,
,
四边形是等角线四边形,
,
在中,,
.
四边形的面积为;
②如图3中,设与相交于点,连接,
作于,于.则,,
四边形是等角线四边形,
,
,
即,
当、重合时,即时,等号成立,
,
,
即线段最大时,四边形的面积最大,
,
,
,
的最大值为6,
当、、共线时,取等号,
四边形的面积的最大值为.
故答案为:18.
【点睛】本题考查四边形综合题、中点四边形、三角形中位线定理、正方形的判定和性质、圆等知识,解题的关键是理解等角线四边形的定义,学会添加常用辅助线,灵活运用所学知识解决问题,属于中考压轴题.
1.我们给出如下定义:顺次连接任意一个四边形各边中所得的四边形叫中点四边形.
(1)如图1,在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,中点四边形EFGH是 .
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点.猜想中点四边形EFGH的形状,并证明你的猜想.
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).
答案:(1)平行四边形;(2)菱形,见解析;(3)正方形
分析(1)连接BD,根据三角形中位线定理证明EH∥FG,EH=FG,根据平行四边形的判定定理证明即可;
(2)证明△APC≌△BPD,根据全等三角形的性质得到AC=BD,再证明EF=FG,根据菱形的判定定理证明结论;
(3)证明∠EHG=90°,利用△APC≌△BPD,得到∠ACP=∠BDP,即可证明∠COD=∠CPD=90°,再根据平行线的性质证明∠EHG=90°,根据正方形的判定定理证明即可.
【详解】解:(1)如图1,连接BD,
∵点E,H分别为边AB,DA的中点,
∴EH∥BD,EH=BD,
∵点F,G分别为边BC,CD的中点,
∴FG∥BD,FG=BD,
∴EH∥FG,EH=GF,
∴中点四边形EFGH是平行四边形,
故答案为:平行四边形;
(2)结论:四边形EFGH是菱形,
理由:如图2,连接AC,BD.
∵∠APB=∠CPD,
∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD,
在△APC和△BPD中,
,
∴△APC≌△BPD(SAS),
∴AC=BD,
∵点E,F,G分别为边AB,BC,CD的中点,
∴EF=AC,FG=BD,
∴EF=FG,
由(1)知中点四边形EFGH是平行四边形,
∴平行四边形EFGH是菱形;
(3)结论:四边形EFGH是正方形,
理由:如图2,设AC与BD交于点O.AC与PD交于点M,
∵△APC≌△BPD,
∴∠ACP=∠BDP,
∵∠DMO=∠CMP,
∴∠COD=∠CPD=90°,
∵EH∥BD,AC∥HG,
∴∠EHG=∠DOC=90°,
由(2)知中点四边形EFGH是菱形,
∴菱形EFGH是正方形.
【点睛】本题考查的是平行四边形的判定和性质、全等三角形的判定和性质、菱形的判定和性质、正方形的判定和性质,解题的关键是灵活应用三角形中位线定理,学会添加常用辅助线.
中考数学几何模型专项复习 模型28 勾股定理——垂美四边形模型-(原卷版+解析): 这是一份中考数学几何模型专项复习 模型28 勾股定理——垂美四边形模型-(原卷版+解析),共16页。
中考数学几何模型专项复习 模型26 勾股定理——378和578模型-(原卷版+解析): 这是一份中考数学几何模型专项复习 模型26 勾股定理——378和578模型-(原卷版+解析),共9页。试卷主要包含了103.等内容,欢迎下载使用。
中考数学几何模型专项复习 模型25 勾股定理——出水芙蓉模型-(原卷版+解析): 这是一份中考数学几何模型专项复习 模型25 勾股定理——出水芙蓉模型-(原卷版+解析),共8页。












