初中数学鲁教版 (五四制)八年级下册2 矩形的性质与判定课堂教学课件ppt

这是一份初中数学鲁教版 (五四制)八年级下册2 矩形的性质与判定课堂教学课件ppt，共16页。PPT课件主要包含了教学目标，知识回顾，矩形的性质，方法1，方法2，方法3，矩形的判定方法，练习一等内容，欢迎下载使用。

1.进一步掌握矩形的性质与判定定理.2.熟练运用性质定理与判定定理解决问题.
教学重点：矩形的判定定理的证明及综合应用.教学难点：矩形的判定的灵活应用 ．
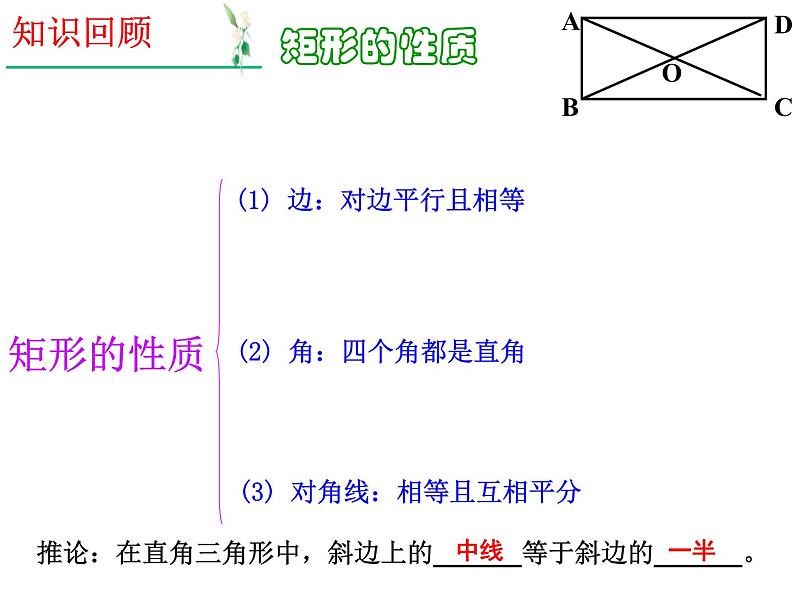
(1) 边：对边平行且相等
(2) 角：四个角都是直角
(3) 对角线：相等且互相平分
推论：在直角三角形中，斜边上的______等于斜边的______。
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
有三个角是直角的四边形是矩形 。
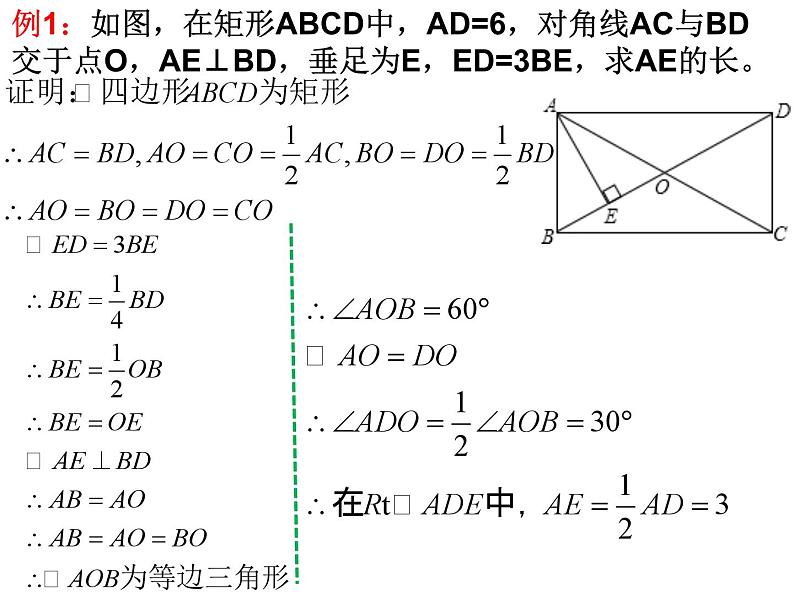
例1：如图，在矩形ABCD中，AD=6，对角线AC与BD交于点O，AE⊥BD，垂足为E，ED=3BE，求AE的长。
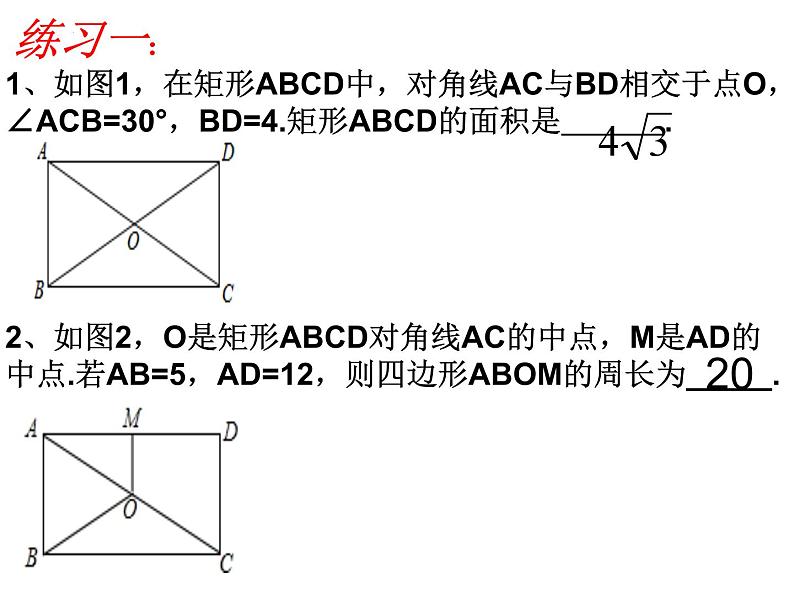
2、如图2，O是矩形ABCD对角线AC的中点，M是AD的中点.若AB=5，AD=12，则四边形ABOM的周长为_____.
1、如图1，在矩形ABCD中，对角线AC与BD相交于点O，∠ACB=30°，BD=4.矩形ABCD的面积是 .
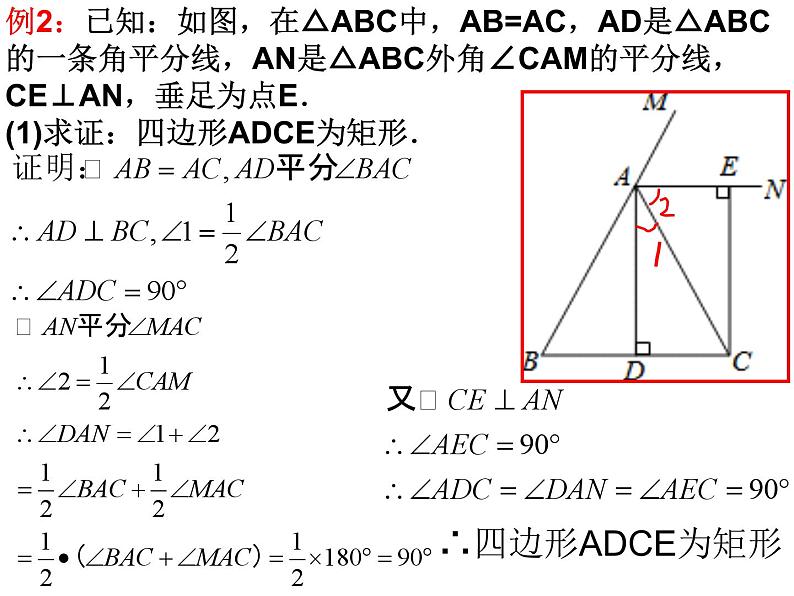
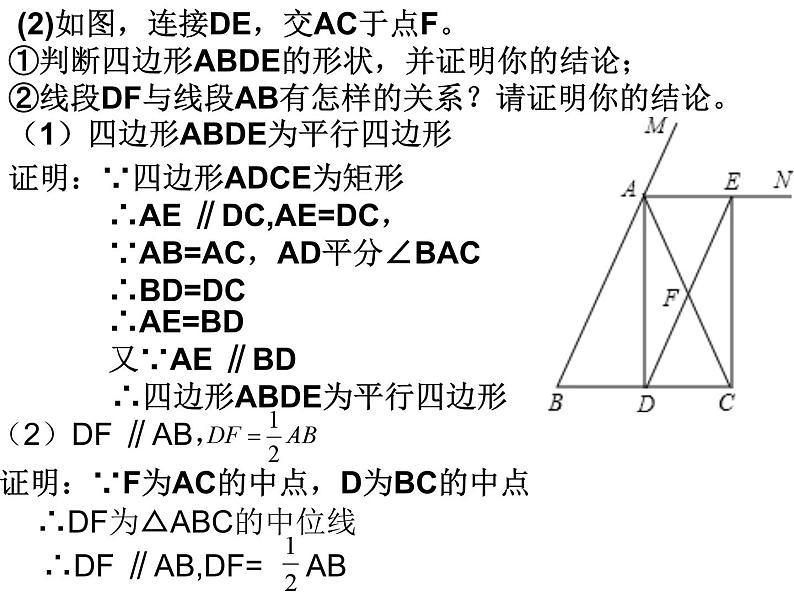
例2：已知：如图，在△ABC中，AB=AC，AD是△ABC的一条角平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．(1)求证：四边形ADCE为矩形．
∴四边形ADCE为矩形
(2)如图，连接DE，交AC于点F。①判断四边形ABDE的形状，并证明你的结论；②线段DF与线段AB有怎样的关系？请证明你的结论。
（1）四边形ABDE为平行四边形
证明：∵四边形ADCE为矩形
∴AE ∥DC,AE=DC，
∵AB=AC，AD平分∠BAC
∴四边形ABDE为平行四边形
证明：∵F为AC的中点，D为BC的中点
∴DF为△ABC的中位线
∴DF ∥AB,DF= AB
练习二：已知：如图，四边形ABCD是由两个全等的等边三角形ABD和CBD组成的，M、N分别是BC和AD的中点.求证：四边形BMDN是矩形.
证明：∵△ABD与△CBD是全等的等边三角形
∴AB=BD,BD=CD,∠ADB=∠BDC=60°
又∵ M、N分别是BC和AD的中点
∴BM ⊥AD,DN ⊥BC,DN平分∠BDC
∴∠MDN=∠ADB+∠BDN=90°
∴∠BMD=∠MDN=∠BND=90°
∴四边形BMDN是矩形
当堂检测1.如图，四边形ABCD的对角线AC、BD相交于点O，已知下列6个条件：①AB∥DC；②AB=DC；③AC=BD；④∠ABC=90°；⑤OA=OC；⑥OB=OD．则不能使四边形ABCD成为矩形的是（　　）A．①②③ B．②③④ C．②⑤⑥ D．④⑤⑥ 2.如图，矩形ABCD 中，AB=4 ，AD=3,折叠纸片使AD 边与对角线 BD重合，折痕为DG ，则 AG的长为 .
3.如图，矩形ABCD 中，对角线AC,BD 交于点O ， 且 求证： BE=CF.
证明：∵四边形ABCD是矩形
∵BE⊥AC且CF⊥BD
∴∠BEO=∠CFO=90°
∴在△BOE与△COF中
∴△BOE≌△COF(AAS)
拓展提升如图，在矩形ABCD中，AB=3，AD=4，P是AD上不与A和D重合的一个动点.过点P分别作AC和BD的垂线，垂足为点E、F.求PE+PF的值.
∵四边形ABCD是矩形，AB=3,AD=4
∴∠BAD=90°，AO=BO=DO=CO
1.（河北）已知下列命题中：（1）矩形是轴对称图形，且有两条对称轴；（2）两条对角线相等的四边形是矩形；（3）有两个角相等的平行四边形是矩形；（4）两条对角线相等且互相平分的四边形是矩形．其中正确的有（　　）A．4个B．3个C．2个D．1个
2.（临沂）如图，△ABC中，AC的垂直平分线分别交AC、AB于点D、F，BE⊥DF交DF的延长线于点E，已知∠A=30°，BC=2，AF=BF，则四边形BCDE的面积是 。
★★★3.（汕头模拟）如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点（且点P不与点B、C重合），PE⊥AB于E，PF⊥AC于F．则EF的最小值为（　　）A．4B．4.8C．5.2D．6