湘教版九年级数学下册 第2章 圆 2.5.4 三角形的内切圆（课件）

这是一份湘教版九年级数学下册 第2章 圆 2.5.4 三角形的内切圆（课件），共15页。

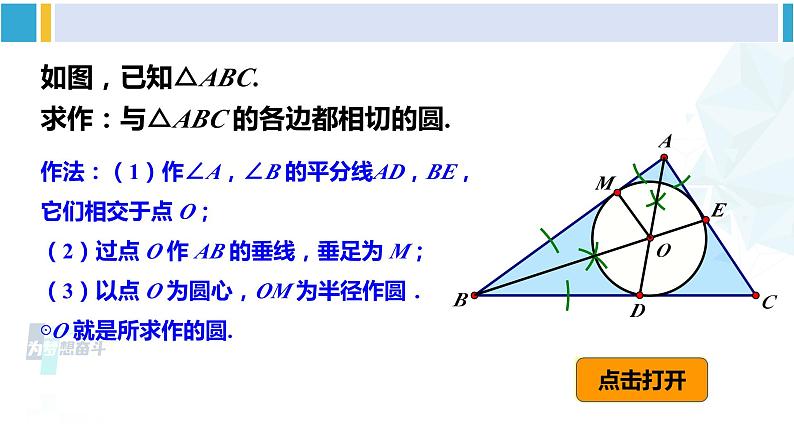
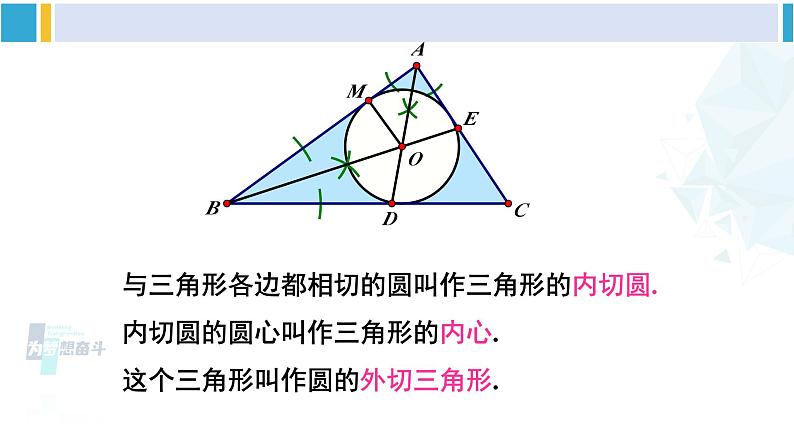
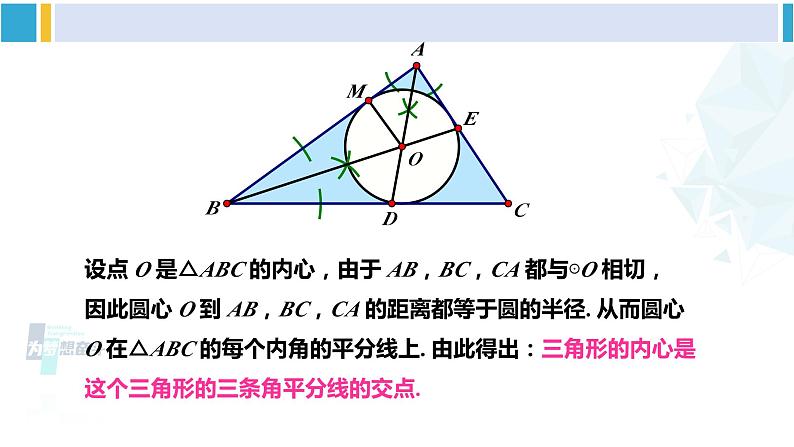
三角形的内切圆湘教·九年级下册如图, 已知△ABC, 请作出△ABC 的三条角平分线.所作的三条角平分线是否相交于一点, 这一点到三角形三边的距离是否相等, 为什么？三角形三条角平分线交点到三边距离相等.点击打开 想在一块三角形硬纸板上剪下一个面积最大的圆形纸板，应当怎样剪？点击打开这使得我们猜测：这个圆应当与三角形的三条边都相切． 与三角形的三条边都相切的圆存在吗？ 若存在， 如何画出这样的圆？如图，已知△ABC.求作：与△ABC 的各边都相切的圆.作法：（1）作∠A，∠B 的平分线AD，BE，它们相交于点 O；（2）过点 O 作 AB 的垂线，垂足为 M；（3）以点 O 为圆心，OM 为半径作圆．⊙O 就是所求作的圆.点击打开与三角形各边都相切的圆叫作三角形的内切圆.内切圆的圆心叫作三角形的内心.这个三角形叫作圆的外切三角形.设点 O 是△ABC 的内心，由于 AB，BC，CA 都与⊙O 相切，因此圆心 O 到 AB，BC，CA 的距离都等于圆的半径. 从而圆心 O 在△ABC 的每个内角的平分线上. 由此得出：三角形的内心是这个三角形的三条角平分线的交点. 如图，⊙O 是△ABC 的内切圆，∠A = 70°，求∠BOC的度数.解∵ ∠A = 70°，∴ ∠ABC +∠ACB = 180° -∠A = 110°.∵ ⊙O 是△ABC 的内切圆，∴ BO，CO 分别是∠ABC与∠ACB 的平分线，即∠1 = ∠ABC， ∠2 = ∠ACB.∴ ∠BOC = 180°-（∠1 +∠2） = 180°- （∠ABC+∠ACB）= 180°- × 110°= 125°.【教材P74页】练习任画一个三角形，求作它的内切圆.【教材P74页】2. 如图，△ABC 的内切圆的三个切点分别为D，E，F， ∠A＝ 74°，∠B ＝ 47°，求圆心角∠EOF 的度数．【教材P74页】解：∵△ABC的内切圆的三个切点分别为D，E，F，∴ OF⊥AC，OE⊥BC，OD⊥AB，∴∠OEC=∠OFC=90°.∵∠A＝ 74°，∠B＝ 47°，∴∠C=59°，∴∠EOF = 121°.3. 已知等边三角形 ABC 的边长为 a， 求它的内切圆的半径．【教材P74页】解：如图，⊙O 是等边三角形ABC 的内切圆，连接OB， OC，则∠OBC＝ ∠B＝30°，∠OCB＝ ∠C＝30°.设BC 边与⊙O 的切点为D，连接OD，则OD⊥BC，且OD 为内切圆的半径.在Rt△OBD 与Rt△OCD 中，∴ BD＝DC， 即 DC＝即内切圆的半径长为随堂练习有下列说法: ①内心一定在三角形内部; ②内心到各顶点的距离相等; ③内心是三角形三个内角平分线的交点; ④内心与外心重合的三角形是等边三角形.其中正确的有（ ） A. 1 个 B. 2 个 C. 3 个 D. 4个选自《创优作业》C2. （眉山中考）如图, 在△ABC 中,∠A ＝ 66°, 点 I 是内心 , 则∠BIC 的大小为（ ） A．114° B．122° C．123° D．132°选自《创优作业》C3. （泉州中考）如图, 点 O 是△ABC 的内心,过点 O 作 EF∥AB, 与 AC, BC 分别交于点 E, F,则（ ） A．EF ＞ AE ＋ BF B．EF ＜ AE ＋ BF C．EF ＝ AE ＋ BF D．EF ≤ AE ＋ BF 选自《创优作业》C课堂小结1.三角形内切圆的作法,2.三角形内切圆的相关概念.