高中数学苏教版 (2019)必修 第二册12.2 复数的运算课后测评

这是一份高中数学苏教版 (2019)必修 第二册12.2 复数的运算课后测评，文件包含122复数的运算原卷版docx、122复数的运算解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。

一、复数的加法
1、加法法则：设z1＝a＋bi，z2＝c＋di(a、b、c、d∈R)是任意两个复数，
规定z1＋z2＝(a＋bi)＋(c＋di)＝(a＋c)＋(b＋d)i.
即两个复数相加，就是实部与实部、虚部与虚部分别相加，显然两个复数的和仍然是复数．
注意：对于复数的加法可以推广到多个复数相加的情形，
即z1＝1＋b1i，z2＝a2＋b2i，z3＝a3＋b3i，…，zn＝an＋bni，
则z1＋z2＋…＋zn＝(a1＋a2＋…＋an)＋(b1＋b2＋…＋bn)i.
2、加法运算律：复数的加法满足交换律、结合律，即对任意的z1、z2、z3∈C，
有z1＋z2＝z2＋z1，(z1＋z2)＋z3＝z1＋(z2＋z3)．
二、复数的减法
1、相反数：已知复数a＋bi(a，b∈R)，根据复数加法的定义，
存在唯一的复数－a－bi，使(a＋bi)＋(－a－bi)＝0.其中－a－bi叫做a＋bi的相反数．
2、减法法则：规定两个复数的减法法则，设z1＝a＋bi，z2＝c＋di(a，b，c，d∈R)是任意两个复数，则z1－z2＝(a＋bi)－(c＋di)＝(a－c)＋(b＋d)i.
即两个复数相减，就是实部与实部、虚部与虚部分别相减，显然两个复数的差仍是一个复数．
三、复数的乘法
1、运算法则：两个复数的乘法可以按照多项式的乘法运算来进行，只是把i2换成－1，
并把最后结果写成a＋bi(a、b∈R)的形式．
设z1＝a＋bi，z2＝c＋di(a、b、c∈R)，则
z1z2＝(a＋bi)(c＋di)＝ac＋adi＋bci＋bdi2＝(ac－bd)＋(ad＋bc)i.
显然两个复数的积仍是复数．
2、复数乘法的运算律：对于任意z1、z2、z3∈C，有
（1）z1·z2＝z2·z1(交换律)；
（2）(z1·z2)·z3＝z1·(z2·z3)(结合律)；
（3）z1·(z2＋z3)＝z1z2＋z1z3(分配律)．
【注意】实数范围内的乘法公式在复数范围内仍然成立．
3、复数的乘方：复数的乘方也就是相同复数的乘积，根据乘法的运算律，实数范围内正整数指数幂的运算律在复数范围内仍然成立．即对复数z1、z2、z和自然数m、n有
zm·zn＝zm＋n，(zm)n＝zm·n，(z1·z2)n＝zeq \\al(n,1)·zeq \\al(n,2)，z0＝1；z－m＝eq \f(1,zm)(z≠0)．
【注意】实数范围内的乘方公式、运算律在复数范围内仍然成立．
四、共轭复数
我们把实部相等，虚部互为相反数的两个复数叫做互为共轭复数．
复数z的共轭复数记作，即时，
【注意】当复数的虚部时，有，也就是，任一实数的共轭复数是它本身.
五、复数的除法
规定两个复数除法的运算法则：（a、b、c、d∈R，c＋di≠0）
a+bi÷c+di=a+bic+di=a+bic−dic+dic−di=ac+bdbc−adic2+d2=ac+bdc2+d2+bc−adc2+d2i
在进行复数除法运算时，通常先把(a＋bi)÷(c＋di)写成eq \f(a＋bi,c＋di)的形式，
再把分子、分母同乘分母的共轭复数c－di，把分母变为实数，化简后就可得到所求结果．
【注意】（1）两个复数相除(除数不为0)，所得的商仍是一个复数．
（2）z＝a＋bi(a，b∈R)，z·eq \x\t(z)＝a2＋b2是复数除法运算中实现分母“实数化”的一个手段．
六、复数方程的解
在复数范围内，实系数一元二次方程ax2+bx+c=0(a≠0)的求解方法：
（1）求根公式法：
= 1 \* GB3 ①当∆≥0时，x=−b±b2−4ac2a = 2 \* GB3 ②当∆<0时，x=−b±−(b2−4ac)i2a
（2）利用复数相等的定义求解，设方程的根为x=m+ni(m，n∈R)，
将此代入方程ax2+bx+c=0(a≠0)，化简后利用复数相等的定义求解。
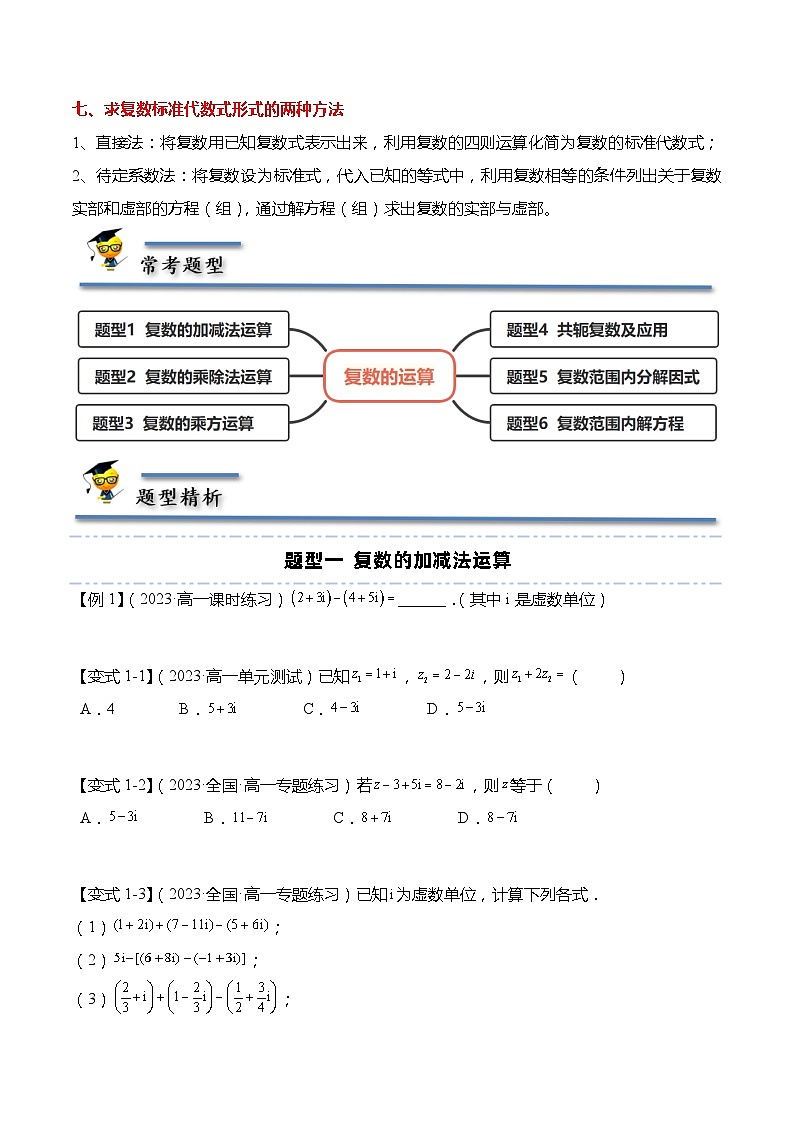
七、求复数标准代数式形式的两种方法
1、直接法：将复数用已知复数式表示出来，利用复数的四则运算化简为复数的标准代数式；
2、待定系数法：将复数设为标准式，代入已知的等式中，利用复数相等的条件列出关于复数实部和虚部的方程（组），通过解方程（组）求出复数的实部与虚部。
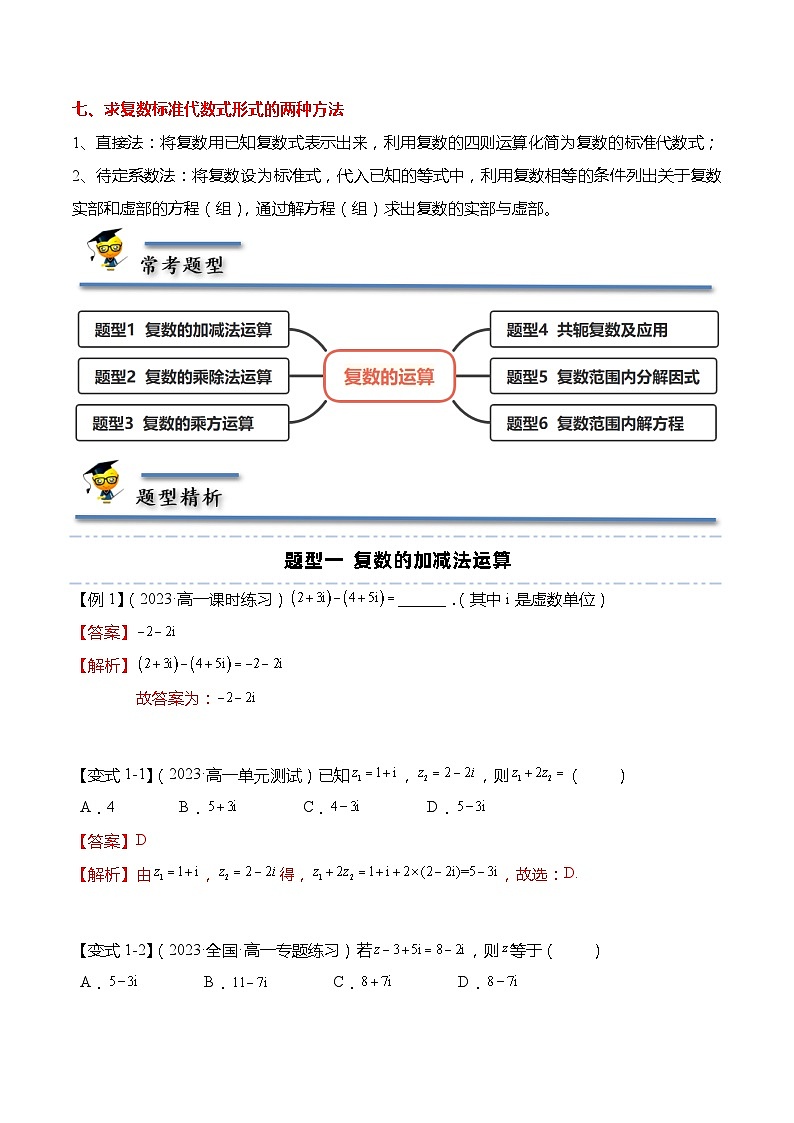
题型一 复数的加减法运算
【例1】（2023·高一课时练习）______．（其中i是虚数单位）
【变式1-1】（2023·高一单元测试）已知，，则（ ）
A．4 B． C． D．
【变式1-2】（2023·全国·高一专题练习）若，则等于（ ）
A． B． C． D．
【变式1-3】（2023·全国·高一专题练习）已知为虚数单位，计算下列各式．
（1）；
（2）；
（3）；
（4）．
题型二 复数的乘除法运算
【例2】（2023·全国·高一专题练习）计算:等于（ ）
A． B． C． D．
【变式2-1】（2022春·山西吕梁·高一校联考期中）设，则复数（ ）
A． B． C． D．
【变式2-2】（2023·高一课时练习）设，则______．
【变式2-3】（2023·全国·高一专题练习）计算下列各题．
（1）；
（2）.
【变式2-4】（2022·高一课时练习）计算：
（1）；
（2）；
（3）．
题型三 复数的乘方运算
【例3】（2022春·新疆乌鲁木齐·高一乌鲁木齐市第70中校考期末）若复数为虚数单位，则（ ）
A． B．1 C． D．
【变式3-1】（2023·高一课时练习）______．（其中i是虚数单位）
【变式3-2】（2023·全国·高一专题练习）若复数满足，则复数的值是______．
【变式3-3】（2023·高一课时练习）已知复数，求的值．
题型四 共轭复数及应用
【例4】（2023·高一单元测试）设复数z满足，则z的虚部为（ ）
A． B． C． D．1
【变式4-1】（2023·全国·高一专题练习）已知复数z满足，则（ ）
A． B． C． D．
【变式4-2】（2023·浙江嘉兴·统考模拟预测）若复数满足，则（ ）
A． B． C． D．
【变式4-3】（2022春·吉林·高一长春校考期中）已知复数，则的共轭复数为_____.
题型五 复数范围内分解因式
【例5】（2022春·福建福州·高一统考期中）多项式在复数集中因式分解的结果是（ ）
A． B．
C． D．
【变式5-1】（2023·高一课时练习）在复数范围内因式分解：______．
【变式5-2】（2022·高一课时练习）在复数范围内分解因式：
（1）； （2）； （3）.
【变式5-3】（2022·高一课时练习）在复数范围内分解因式：
（1） （2） （3） （4）
题型六 复数范围内解方程
【例6】（2023·高一课时练习）若关于的方程有虚根，则实数的取值范围是______．
【变式6-1】（2023·高一单元测试）若复数是方程的一个根，则的虚部为（ ）
A．2 B． C． D．
【变式6-2】（2022·高一单元测试）已知是关于的实系数一元二次方程的一个根，则___________.
【变式6-3】（2023·高一课时练习）关于的一元二次方程至少有一个实根，则实数的值是______．