




初中人教版5.3.1 平行线的性质教案配套ppt课件
展开1.知道平行线的性质2.能应用平行线的性质进行简单的计算和推理(重点)
它与地面所成的较大的角∠3是多少度呢?
图中为世界著名的意大利比萨斜塔,为8层圆柱形建筑,
目前,它与地面所成的较小的角为∠1=85°,
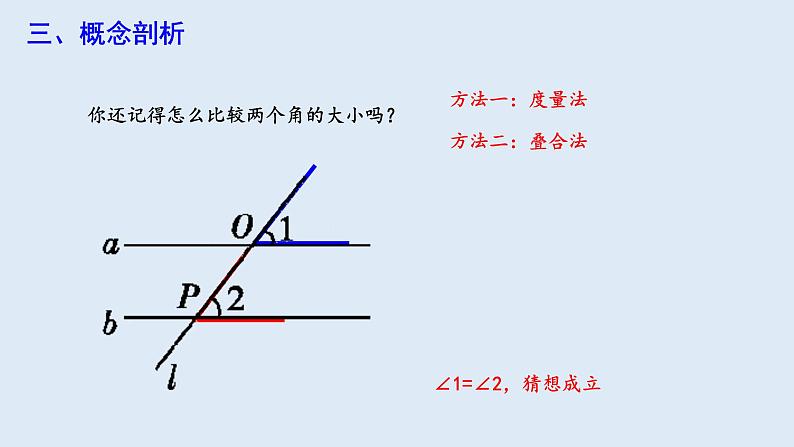
如图,如果直线a与直线b平行,直线l与直线a、b分别交于点O、点P,那么图中的∠1与∠2有什么关系?
猜想:∠1、∠2是同位角,且相等.
你还记得怎么比较两个角的大小吗?
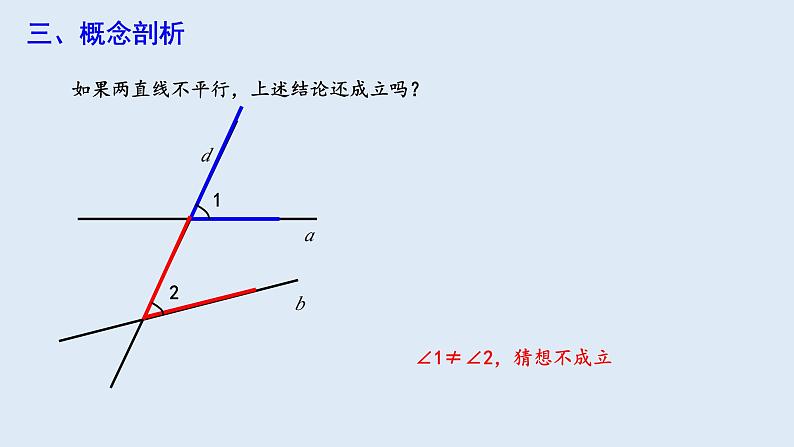
如果两直线不平行,上述结论还成立吗?
∠1≠∠2,猜想不成立
一般地,平行线具有性质:性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
如图,∵ a//b (已知)
∴∠1=∠2(两直线平行,同位角相等)
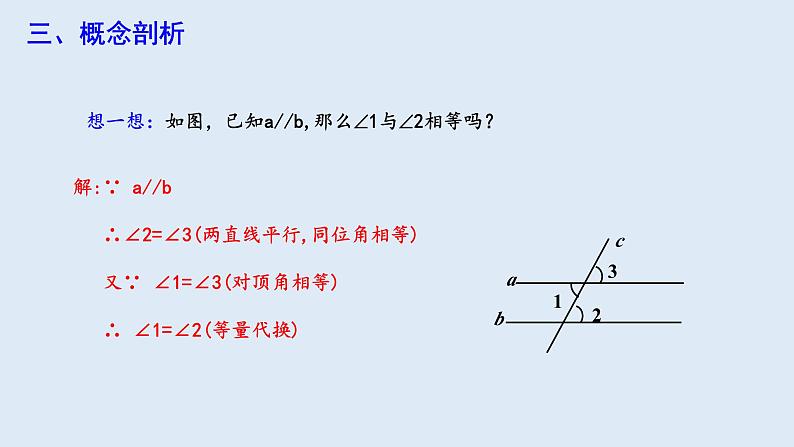
想一想:如图,已知a//b,那么1与2相等吗?
解:∵ a//b ∴∠2=∠3(两直线平行,同位角相等) 又∵ ∠1=∠3(对顶角相等) ∴ ∠1=∠2(等量代换)
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
如图,∵ a//b (已知)
∴∠1=∠2(两直线平行,内错角相等)
想一想:如图,已知a//b,那么2与4互补吗?
解:∵a//b
∴2+4=180°(等量代换)
∵ 1+4=180°(邻补角定义)
∴1=2(两直线平行,同位角相等)
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∴∠2+∠4=180°(两直线平行,同旁内角互补)
例1.如图,某玻璃碎片是梯形,AD∥BC,已有上底的一部分,量得∠D=115°.
(1)你能求∠C的度数吗?
解:∵AD∥BC(已知),
∴∠C=65°(等式的性质).
∴115°+∠C=180°(等量代换),
∵∠D=115°(已知),
∴∠D+∠C=180°(两直线平行,同旁内角互补).
已知:如图,某玻璃碎片是梯形,AD∥BC,已有上底的一部分.∠D=115°.
(2)上题中你能求出∠B的度数吗?请说明理由.
解:不能,因为结合已有条件:
给出∠A或∠B的角度,那该梯形的四个角度都可以求出.
若可以再添加一个条件:
我们仍然无法得到∠B和∠A的角度,
AD∥BC,∠D=115°,∠C=65°,
1.如图,AB∥CD ,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=62°,则∠GEF等于( )
A.36° B.59° C.62 ° D.118°
2.如图,直线a∥b,若∠1=70°,则∠2的度数是多少?
解:∵a∥b(已知),
∴∠2=180°-∠1=180°-70°=110°(等式的性质).
∵∠1=70°(已知),
∴∠1+∠2=180°(两直线平行,同旁内角互补),
例2.如图,直线AB∥CD,∠1=45°,∠6的度数是多少?
解:∵AB∥CD(已知),
∴∠6=180°-∠5=180°-45°=135°(等式的性质).
∵∠5+∠6=180°(互为补角),
∴∠1=∠5=45°(两直线平行,同位角相等).
思考:你能利用平行线的另外两条性质解题吗?
3.如图,AB∥CD,截线EF与AB、CD分别相交于M、N两点,∠7∶∠8=1∶2,则∠1,∠2分别等于( )
A.60°,120° B.30°,150° C.20°,160° D.40°,140°
4.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴DG∥AB(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∴∠AGD=180°-∠BAC=180°-70°=110°.
初中数学人教版七年级下册5.3.1 平行线的性质背景图ppt课件: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c88546_t3/?tag_id=26" target="_blank">5.3.1 平行线的性质背景图ppt课件</a>,共24页。PPT课件主要包含了成果展示,书写格式,平行线的性质,得出结论,平行线的性质3,∵a∥b,符号语言,简写为,两直线平行,ABCD等内容,欢迎下载使用。
初中数学人教版七年级下册5.3.1 平行线的性质课文配套ppt课件: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c88546_t3/?tag_id=26" target="_blank">5.3.1 平行线的性质课文配套ppt课件</a>,共19页。PPT课件主要包含了学习目标,新课导入,概念剖析,方法一度量法,方法二叠合法,∠1∠2猜想成立,归纳总结,应用格式,典型例题,当堂检测等内容,欢迎下载使用。
初中数学5.3.1 平行线的性质教学课件ppt: 这是一份初中数学<a href="/sx/tb_c88546_t3/?tag_id=26" target="_blank">5.3.1 平行线的性质教学课件ppt</a>,共39页。PPT课件主要包含了两直线平行,同位角,内错角,同旁内角,平行线,基础巩固等内容,欢迎下载使用。













