初中数学人教版七年级下册5.3.1 平行线的性质集体备课ppt课件

这是一份初中数学人教版七年级下册5.3.1 平行线的性质集体备课ppt课件，共19页。PPT课件主要包含了学习目标，课时讲解，课时流程，知识点，平行线的性质1，感悟新知，平行线的性质2，平行线的性质3等内容，欢迎下载使用。

平行线的性质1平行线的性质2平行线的性质3
1. 性质1：两条平行线被第三条直线所截，同位角相等 .简单说成：两直线平行，同位角相等.表达方式：如图5.3-1，因为a ∥ b(已知)，所以∠ 1= ∠ 2(两直线平行，同位角相等).
2. 平行线的性质与平行线的判定的区别：(1)平行线的判定是根据两角的数量关系得到两条直线的位置关系，而平行线的性质是根据两条直线的位置关系得到两角的数量关系；(2)平行线的判定的条件是平行线的性质的结论，而平行线的判定的结论是平行线的性质的条件.
特别警示●两条直线平行是前提，只有在这个前提下才有同位角相等；●格式书写时，顺序不能颠倒，与判定不能混淆.
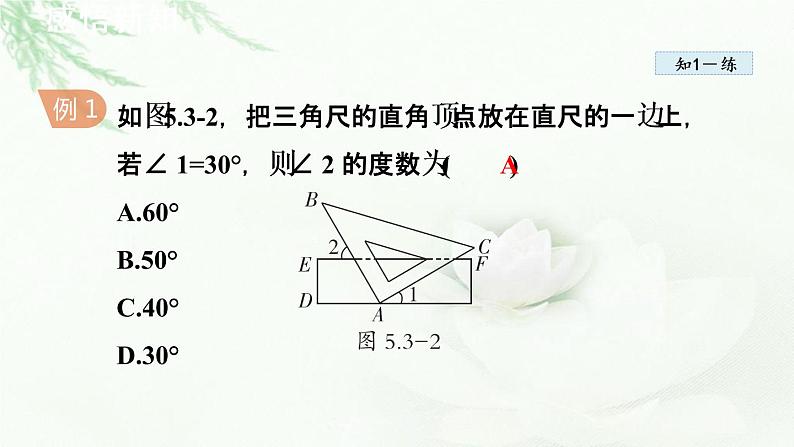
如图5.3-2，把三角尺的直角顶点放在直尺的一边上，若∠ 1=30°，则∠ 2 的度数为( )A.60° B.50° C.40° D.30°
解：∵∠ 1+ ∠ BAC+ ∠ DAB=180°，∠ BAC=90°，∠ 1=30°，∴∠ DAB=180°－∠ 1－∠ BAC=60°.∵直尺的对边平行，即EF ∥ AD，∴ ∠ 2= ∠ DAB=60°.
解题秘方：根据直尺的对边平行，利用平行线的性质建立已知角∠ 1 与待求的角∠ 2 之间的数量关系.
1-1.[中考·柳州] 如图，直线a，b 被直线c 所截，若a ∥ b， ∠ 1=70 °，则∠ 2 的度数是( )A. 50° B. 60°C. 70° D. 110°
1. 性质2：两条平行线被第三条直线所截，内错角相等.简单说成：两直线平行，内错角相等.2. 表达方式：如图5.3-3，因为a ∥ b(已知)，所以∠ 1= ∠ 2(两直线平行，内错角相等).
特别警示并不是所有的内错角都相等，只有在“两直线平行”的前提下，才有内错角相等.
如图5.3-4，AB ∥ CD，BE 平分∠ ABC，CF 平分∠ BCD，你能发现BE 和CF 有何特殊的位置关系吗？说说你的理由.
解题秘方：由两直线平行得到内错角相等，再由内错角相等得到两直线平行.
解：BE∥CF.理由如下：∵ AB∥CD(已知)，∴∠ ABC= ∠ BCD (两直线平行，内错角相等).∵ BE 平分∠ ABC，CF 平分∠ BCD (已知)，∴∠ 2= ∠ ABC，∠ 1= ∠ BCD (角平分线的定义).∴∠ 2= ∠ 1. ∴ BE ∥ CF (内错角相等，两直线平行).
2-1. 如图，已知AB ∥CD，∠ ADC= ∠ ABC.试说明∠ E= ∠ F.
解：∵AB∥CD，∴∠ABC＝∠DCF.又∵∠ADC＝∠ABC，∴∠ADC＝∠DCF，∴DE∥BF.∴∠E＝∠F.
1. 性质3：两条平行线被第三条直线所截，同旁内角互补.简单说成：两直线平行，同旁内角互补.2. 表达方式：如图5.3-5，因为a ∥ b(已知)，所以∠ 1+ ∠ 2=180° (两直线平行，同旁内角互补).
警示误区两直线平行时，同旁内角是互补的关系而不是相等的关系
[中考·黄冈] 已知：如图5.3-6，直线a ∥ b，∠ 1=50°，∠ 2= ∠ 3，则∠ 2 的度数为( )A.50° B.60° C.65° D.75°
解题秘方：由平行线的性质找出∠ 1 与∠ 2和∠ 3 之间的数量关系，利用∠ 1 的度数求出∠ 2 的度数.
解：∵ a ∥ b， ∴∠ 1+ ∠ 2+ ∠ 3=180°.又∵∠ 1=50°，∴∠ 2+ ∠ 3=130°. ∴∠ 2=65°.
3-1.[中考·西藏] 如图，l1 ∥l2，∠ 1=38°，∠ 2＝46 °， 则∠ 3 的度数为( )A. 46° B. 90°C. 96° D. 134°