

湖南省娄底市新化县2023-2024学年九年级上学期期末数学试题
展开考试时间:120分钟;分值:120分
一、单选题(本大题共10道小题,每小题3分,满分30分.每道小题给出的四个选项中,只有一项是符合题设要求的,请把你认为符合题目要求的选项填涂在答题卡上)
1.下列函数中,y是x的反比例函数的是( )
A. B. C. D.
2.若一元二次方程的一个根为,则a的值为( )
A.2 B. C.4 D.
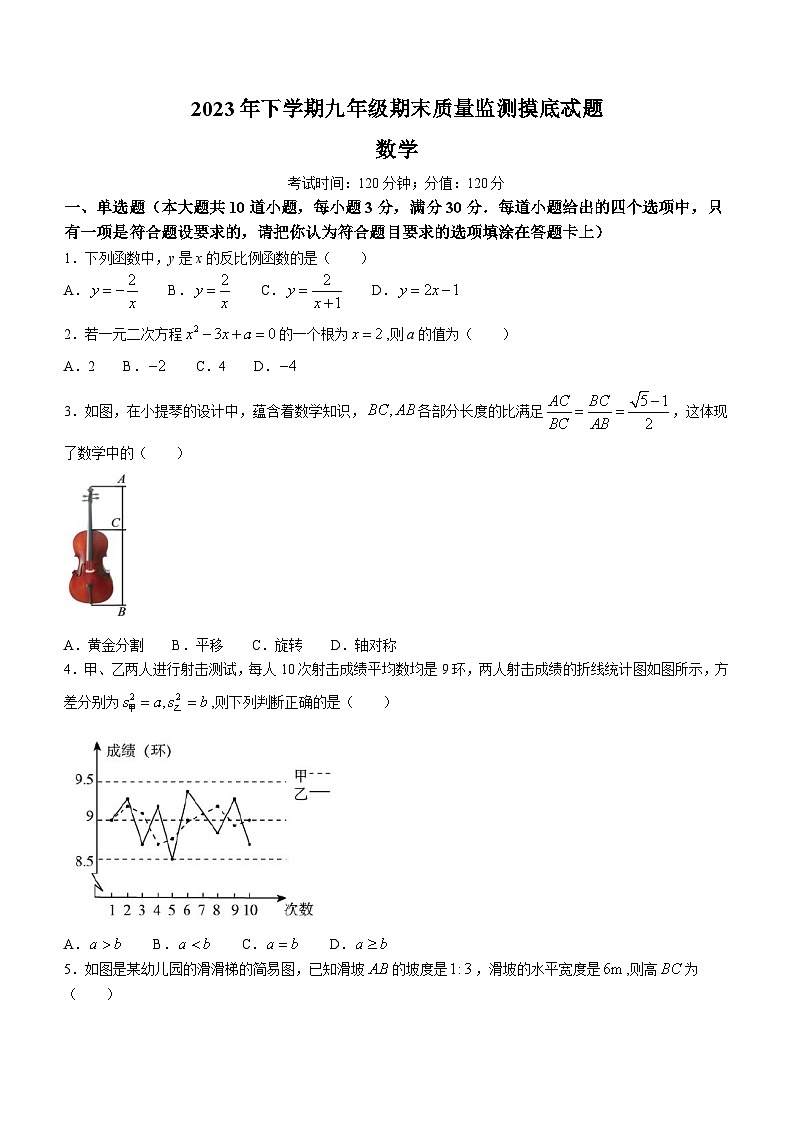
3.如图,在小提琴的设计中,蕴含着数学知识,各部分长度的比满足,这体现了数学中的( )
A.黄金分割 B.平移 C.旋转 D.轴对称
4.甲、乙两人进行射击测试,每人10次射击成绩平均数均是9环,两人射击成绩的折线统计图如图所示,方差分别为,则下列判断正确的是( )
A. B. C. D.
5.如图是某幼儿园的滑滑梯的简易图,已知滑坡的坡度是,滑坡的水平宽度是,则高为( )
A. B. C. D.
6.已知与相似,且周长比为,则与的面积比为( )
A. B. C. D.
7.抛物线的对称轴是直线( )
A. B. C. D.
8.如图,的顶点是正方形网格的格点,则的值为( )
A. B. C.1 D.
9.已知中半径,则弦的长度为( )
A.3 B. C. D.
10.如图,在平面直角坐标系中,函数与的图象交于A,B两点,过A作y轴的垂线,交函数的图象于点C,连接,则的面积为( )
A.1 B.3 C.5 D.7
二、填空题(本大题共6道小题,每小题3分,满分18分,请把答案写在答题卡上)
11.已知反比例函数的图象经过点,则k的值是____________.
12.若数据3,x,4,5的众数和中位数都是4,则这组数据的方差是____________.
13.如图,四边形四边形,则的度数为____________.
14.如图,用直角曲尺可以检查半圆形的工件是否合格,其中的数学依据是____________.
15.《中秋帖》是晋朝书法家王献之的作品,如图,在一幅长为,宽为的《中秋帖》矩形书法作品的四周镶上相同宽度的金色纸边,制成一幅矩形挂图,设金色纸边的宽为,如果要使整个挂图的面积是,那么x满足的方程是____________.
16.二次函数的图象如图所示,①;②;③;④;⑤当时,.其中正确的是____________.(填序号)
三、解答题(本大题共66分,17,18,19题各6分;20,21题各8分;22,23题各9分;24,25题各10分,请把解答过程书写在答题卡上)
17.计算:.
18.小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角,为节省家里空间,小明想把垃圾桶放到桌下,经测量桌子下沿离地面高,垃圾桶高,桶盖直径,当垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(参考数据:)
19.如图所示,已知为圆O的直径,是弦,且于点E,连接.
(1)求证:;
(2)若,求圆O的直径.
20.为提升学生的核心素养,某教育教学联合体开展了城乡读书交流活动.该教育教学联合体的某成员校号召全体师生积极捐书.为了解所捐书的种类,校团委对部分书籍进行了随机抽样调查,所捐书籍分为四类:文学类(记作A类),艺术类(记作B类),科普类(记作C类),其他类(记作D类).学生张华根据收集的数据绘制了如图1,图2所示的不完整的统计图,请根据统计图提供的信息,解答下面的问题:
图1 图2
(1)本次随机抽样调查的书籍的本数是____________本;____________;D类扇形圆心角的度数等于____________°;
(2)通过计算,补全图①中的条形统计图.
(3)本次活动,该校一共捐书1000本,请你估计文学类的书籍约有多少本?
21.如图,中,是边上的高,.作矩形,使它的一边在上,顶点G,H分别在上,与的交点为M,且矩形长是宽的2倍.
(1)求证:;
(2)试求矩形的周长.
22.第19届亚运会于2023年9月23日在中国杭州举行,某商场在销售亚运会吉祥物徽章时发现,当每套徽章盈利40元时,则每天可售出20套.为了喜迎亚运会,商场决定采取适当的降价措施,经调查发现,如果销售单价每降价1元,该商店平均每天将多销售2套.
(1)当每套徽章盈利38元时,每天可多销售多少套?
(2)商场为了尽快减少库存,每套吉祥物徽章降价多少元时,该商场销售吉祥物徽章的日盈利可达到1200元?
23.若关于x的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.例如:已知一元二次方程的两个根是和,则该方程是“倍根方程”.
(1)若一元二次方程是“倍根方程”,求c的值;
(2)若是“倍根方程”,求代数式的值.
24.如图,一次函数与反比例函数的图象分别交于点和点,与坐标轴分别交于点C和点D.
(1)求一次函数与反比例函数的表达式;
(2)直接写出不等式的解集.
(3)在x轴上是否存在点P,使与相似,若存在,求出点P的坐标;若不存在,请说明理由.
25.如图,直线与x轴交于点C,与y轴交于点B,抛物线经过B,C两点,与x轴交于另一点A,点E是直线上方抛物线上的一动点,过E作轴交x轴于点F,交直线于点M.
(1)求抛物线的解析式;
(2)求线段的最大值;
(3)在(2)的条件下,连接,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,A,M为顶点的四边形为平行四边形?如果存在,请直接写出P点的坐标;如果不存在请说明理由.
2023年下学期九年级期末质量监测摸底
数学参考答案
一、选择题(30分)
二、填空题(18分)
11. 12.0.5 13. 14.直径所对的圆周角为直角
15. 16.①③⑤
三、解答题(17、18、19各6分,20、21各8分,22、23各9分,24、25各10分,共72分)
17.解:原式 4分
. 6分
18.解:如图所示,过点C作分别交于F、H,则四边形是矩形,
,
在中,,
,
,
,
∴桶盖完全打开没有碰到桌子下沿. 6分
19.解:(1)证明:为的直径,,
,
,
,
,
; 3分
(2)设的半径为,则,
.
在中,由勾股定理可得
,即,
解得,
.
故圆O的直径为. 6分
20.解:(1)解:本次抽样调查的书有(本);
A类所占百分比为,
D类所占百分比为,
D类扇形圆心角的度数为,
故答案为:100,25,54; 3分
(2)随机抽样调查B类书的数量为(本),
补全统计图如下:
某校师生捐书种类扇形统计图
6分
(3)估计文学类(D类)书籍的本数为(本). 8分
21.(1)证明:∵四边形为矩形,
,
而,
,
,
; 4分
(2)解:设,
则,解得,
∴这个矩形的周长. 8分
22.(1)解:(套)
答:当每套徽章盈利38元时,每天可多销售4套. 3分
(2)解:设每套吉祥物徽章降价x元时,商场销售吉祥物徽章日盈利可达到1200元,
根据题意得:,
整理得:,
解得,
∴题目要求尽快减少库存,
(舍去),
,
答:每套徽章降价20元时,商场销售吉祥物徽章日盈利可达到1200元. 9分
23.解:(1)解:设一元二次方程的一个根为,则另一个根为,
∴由根与系数的关系得,,
解得,,即一个根为1,另一个根为2,
. 3分
(2)解:,
, 5分
当时,,原式,
当时,,原式. 9分
24.解:(1)把代入反比例函数,得
∴反比例函数的表达式. 2分
∵点在图象上,,即
把两点代入,
解得
所以一次函数的表达式为. 4分
(2) 6分
(3)由(1)得一次函数的表达式为
当时,,即.
当=0时,点坐标为,即,
.
.
设P点坐标为,由题可以,点P在点D左侧,则,
由可得:
①当时,,
解得,故点P坐标为; 8分
②当时,,
解得,即点P的坐标为.
因此,点P的坐标为或时,与相似. 10分
25.(1)解:直线与x轴交于点C,与y轴交于点B,
当时,,即B的坐标为,
当时,,解得,即C的坐标为,
将代入抛物线中,
有,解得,
故抛物线的解析式为; 3分
(2)解:设点E的横坐标为m,
∵点E是直线上方拋物线上的一动点,
,
轴,且点M在直线上,直线解析式为,
∴点E和点M的横坐标相同,则,
则有:,
,
∴当时,有最大值,最大值为18,此时;
即最大值为18; 6分
(3)解:存在,理由如下:
根据(2)的结论可知:当时,有M的坐标为:,
∵抛物线的解析式为,
∴抛物线的对称轴为:,
令,解得或者,即可得A坐标为:,
根据点Q是抛物线对称轴上的动点,设Q的坐标为:,
根据点P是抛物线上的点,设P的坐标为:,
以为顶点的四边形为平行四边形,此时分类讨论:
第一种情况:以为对角线时,另一条对角线为,
根据平行四边形的对角线互相平分和中点坐标公式可得:,解得:,则可得P点坐标为:;
第二种情况:以为对角线时,另一条对角线为,
-1+t根据平行四边形的对角线互相平分和中点坐标公式可得:,解得:,则可得P点坐标为:;
第三种情况:以为对角线时,另一条对角线为,
根据平行四边形的对角线互相平分和中点坐标公式可得:,解得:,则可得P点坐标为:;
综上:P点坐标为:或者. 10分题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
A
B
C
D
B
D
A
C
湖南省娄底市新化县2023-2024学年七年级上学期期末数学试题(含解析): 这是一份湖南省娄底市新化县2023-2024学年七年级上学期期末数学试题(含解析),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
湖南省娄底市新化县2023-2024学年九年级上学期期末数学试题(含答案): 这是一份湖南省娄底市新化县2023-2024学年九年级上学期期末数学试题(含答案),共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
湖南省娄底市新化县2023-2024学年八年级上学期期末数学试题(含答案): 这是一份湖南省娄底市新化县2023-2024学年八年级上学期期末数学试题(含答案),共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












