湖南省娄底市新化县2024年九年级数学第一学期开学监测试题【含答案】

这是一份湖南省娄底市新化县2024年九年级数学第一学期开学监测试题【含答案】，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）七位评委对参加普通话比赛的选手评分，比赛规则规定要去掉一个最高分和一个最低分，然后计 算剩下了 5 个分数的平均分作为选手的比赛分数，规则“去掉一个最高分和一个最低分”一定不会影 响这组数据的（ ）
A．平均数B．中位数C．极差D．众数
2、（4分）在平面直角坐标系中，点A、B、C、D是坐标轴上的点，，点，，点在如图所示的阴影部分内部(不包括边界)，则a的取值范围是( )
A．B．C．D．
3、（4分）下列关于变量的关系，其中不是的函数的是（ ）
A．
B．
C．
D．
4、（4分）如图，在平行四边形ABCD中，点E是CD边上一点，，连接AE、BE、BD，且AE、BD交于点F，若，则（ ）
A．15.5B．16.5C．17.5D．18.5
5、（4分）如图，在菱形ABCD中，∠BAD＝60°，AB＝2，E是DC边上一个动点，F是AB边上一点，∠AEF＝30°．设DE＝x，图中某条线段长为y，y与x满足的函数关系的图象大致如图所示，则这条线段可能是图中的（ ）．
A．线段ECB．线段AEC．线段EFD．线段BF
6、（4分）甲、乙、丙、丁四位选手各射击10次，每人的平均成绩都是9.3环，方差如下表所示：
则这四人中成绩最稳定的是（ ）
A．甲B．乙C．丙D．丁
7、（4分）若，则下列变形错误的是（ ）
A．B．C．D．
8、（4分）某汽车制造厂为了使顾客了解一种新车的耗油量，公布了调查20辆该车每辆行驶100千米的耗油量，在这个问题中总体是（ ）
A．所有该种新车的100千米耗油量B．20辆该种新车的100千米耗油量
C．所有该种新车D．20辆汽车
二、填空题（本大题共5个小题，每小题4分，共20分）
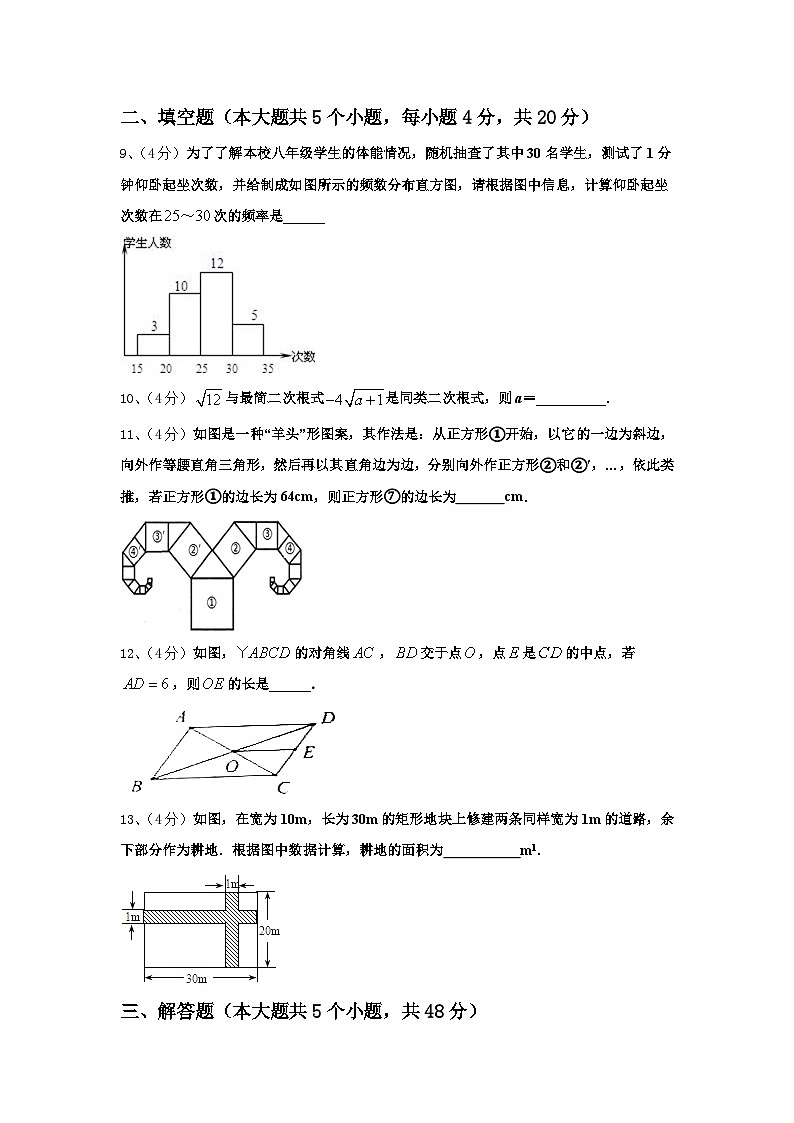
9、（4分）为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐次数，并给制成如图所示的频数分布直方图，请根据图中信息，计算仰卧起坐次数在次的频率是______
10、（4分）与最简二次根式是同类二次根式，则a＝__________.
11、（4分）如图是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②′，…，依此类推，若正方形①的边长为64cm，则正方形⑦的边长为 cm．
12、（4分）如图，的对角线，交于点，点是的中点，若，则的长是______.
13、（4分）如图，在宽为10m，长为30m的矩形地块上修建两条同样宽为1m的道路，余下部分作为耕地．根据图中数据计算，耕地的面积为 m1．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图1，平面直角坐标系中，直线AB：y=﹣x+b交x轴于点A(8，0)，交y轴正半轴于点B．
(1)求点B的坐标；
(2)如图2，直线AC交y轴负半轴于点C，AB=BC，P为线段AB上一点，过点P作y轴的平行线交直线AC于点Q，设点P的横坐标为t，线段PQ的长为d，求d与t之间的函数关系式；
(3)在(2)的条件下，M为CA延长线上一点，且AM=CQ，在直线AC上方的直线AB上是否存在点N，使△QMN是以QM为斜边的等腰直角三角形？若存在，请求出点N的坐标及PN的长度；若不存在，请说明理由.
15、（8分）如图，已知点A在反比例函数（x＞0）的图像上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图像经过点A，与y轴的正半轴交于点B．
（1）求点A的坐标；
（2）若四边形ABOC的面积是，求一次函数y=kx+b的表达式．
16、（8分）如图1，在矩形ABCD中，AB=4，AD=5，E为射线BC上一点，DF⊥AE于F，连结DE．
（1）当E在线段BC上时
①若DE=5，求BE的长；
②若CE=EF，求证：AD=AE；
（2）连结BF，在点E的运动过程中：
①当△ABF是以AB为底的等腰三角形时，求BE的长；
②记△ADF的面积为S1，记△DCE的面积为S2，当BF∥DE时，请直接写出S1：S2的值．
17、（10分）在平面直角坐标系中，一次函数y=kx+b（k，b都是常数，且k≠0）的图象经过点（1，0）和（0，2）．
（1）当﹣2＜x≤3时，求y的取值范围；
（2）已知点P（m，n）在该函数的图象上，且m﹣n=4，求点P的坐标．
18、（10分）如图，E是平行四边形ABCD的边BA延长线上一点，AE=AB，连结AC、DE、CE．
（1）求证：四边形ACDE为平行四边形．
（2）若AB=AC，AD=4，CE=6，求四边形ACDE的面积．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）点P（m+2，2m+1）向右平移1个单位长度后，正好落在y轴上，则m＝_____．
20、（4分）定义一种运算法则“”如下：，例如：，若，则的取值范围是____________.
21、（4分）一只不透明的袋子中有1个白球、1个红球和2个黄球，这些球除颜色不同外其它都相同．搅均后从中任意摸出1个球，摸出白球可能性______摸出黄球可能性．（填“等于”或“小于”或“大于”）．
22、（4分）函数y＝中，自变量x的取值范围是________．
23、（4分）如图，矩形中，，延长交于点，延长交于点，过点作，交的延长线于点，，则=_________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在平面直角坐标系中，O为坐标原点，直线l1：y=kx+4与y轴交于点A，与x轴交于点B．
（1）请直接写出点A的坐标：______；
（2）点P为线段AB上一点，且点P的横坐标为m，现将点P向左平移3个单位，再向下平移4个单位，得点P′在射线AB上．
①求k的值；
②若点M在y轴上，平面内有一点N，使四边形AMBN是菱形，请求出点N的坐标；
③将直线l1绕着点A顺时针旋转45°至直线l2，求直线l2的解析式．
25、（10分）阅读材料，解决问题
材料一：《孟子》中记载有一尺之棰，日取其半，万世不竭，其中蕴含了“有限”与“无限”的关系.如果我们要计算到第n天时，累积取走了多长的木棒？可以用下面两种方法去解决：
方法一：第n天，留下了尺木棒，那么累积取走了尺木棒.
方法二：第1天取走了尺木棒，第2天取走了尺木棒，……第n天取走了尺木棒，那么累积取走了：尺木棒.
设：……①
由①×得：……②
①－②得： 则：
材料二：关于数学家高斯的故事，200多年前，高斯的算术老师提出了下面的问题：1+2+3+…+100=？据说当其他同学忙于把100个数逐项相加时，十岁的高斯却用下面的方法迅速算出了正确的答案：（1+100）+（2+99）+…+（50+51）=101×50=5050.
也可以这样理解：令S=1+2+3+4+…+100 ①，则S=100+99+98+…+3+2+1②
①+②得：2S=（1+100）+（2+99）+（3+98）+…+（100+1）=100×（1+100）
即
请用你学到的方法解决以下问题：
（1）计算：；
（2）我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层的2倍，问塔的顶层共有多少盏灯？
（3）某中学“数学社团”开发了一款应用软件，推出了“解数学题获取软件激活码”的活动，某一周，这款软件的激活码为下面数学问题的答案：已知一列数1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，……其中第1项是，接下来的两项是，，再接下来的三项是，，，以此类推，求满足如下条件的正整数N：，且这一列数前N项和为2的正整数幂，请求出所有满足条件的软件激活码正整数N的值.
26、（12分）如图，经过点的一次函数与正比例函数交于点．
（1）求，，的值；
（2）请直接写出不等式组的解集．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
根据平均数、中位数、极差及众数的意义分别判断后即可确定正确的选项．
【详解】
去掉一个最高分和一个最低分一定会影响到平均数、极差，可能会影响到众数，
一定不会影响到中位数，
故选B.
此题考查统计量的选择，解题关键在于掌握各性质定义.
2、D
【解析】
只要求出点B的横坐标以及直线AD与直线BC交点的横坐标值即可.
【详解】
解：在直角三角形AOB中，根据勾股定理得，

设直线AD的解析式为 ，将代入得：
，解得，所以直线AD的解析式为
同理由，两点坐标可得直线BC的解析式为
联立得，解得 ，所以直线AD与直线BC交点坐标为.
因为点B与直线AD与直线BC交点处于阴影部分的最边界，所以由题意可得.
故选：D
本题考查了平面直角坐标系及一次函数，灵活应用待定系数法求函数解析式是解题的关键.
3、D
【解析】
根据函数的定义，设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量，进而判断得出即可．
【详解】
解：选项ABC中，对于x的每一个确定的值，y都有唯一的值与其对应，故y是x的函数；
只有选项D中，x取1个值，y有2个值与其对应，故y不是x的函数．
故选D．
此题主要考查了函数的定义，正确掌握函数定义是解题关键．
4、C
【解析】
根据已知可得到相似三角形，从而可得到其相似比，根据相似三角形的面积比等于相似比的平方求出△ABF，再根据同高的三角形的面积之比等于底的比得出△BEF的面积，则= +即可求解.
【详解】
解：∵四边形ABCD是平行四边形，
∴DE∥AB，
∴△DFE∽△BFA，
∵DE：EC=2：3，
∴DE：AB=2：5，DF：FB=2：5，
∵=2，根据相似三角形的面积比等于相似比的平方，
∴： =，即==12.5，
∵同高的三角形的面积之比等于底的比，△DEF和△BEF分别以DF、FB为底时高相同，
∴：= DF：FB=2：5，即==5，
∴= +=12.5+5=17.5，
故选C．
本题考查了相似三角形的性质，相似三角形的面积比等于相似比的平方，同高的三角形的面积之比等于底的比，解题的关键是掌握相似三角形的性质．
5、B
【解析】
分析：求出当点E与点D重合时，即x=0时EC、AE、EF、BF的长可排除C、D；当点E与点C重合时，即x=2时，求出EC、AE的长可排除A，可得答案．
详解：当点E与点D重合时，即x=0时，EC=DC=2，AE=AD=2，
∵∠A=60°，∠AEF=30°，
∴∠AFD=90°，
在Rt△ADF中，∵AD=2，
∴AF=AD=1，EF=DF=ADcs∠ADF=，
∴BF=AB-AF=1，结合图象可知C、D错误；
当点E与点C重合时，即x=2时，
如图，连接BD交AC于H，
此时EC=0，故A错误；
∵四边形ABCD是菱形，∠BAD=60°，
∴∠DAC=30°，
∴AE=2AH=2ADcs∠DAC=2×2×=2，故B正确．
故选：B．
点睛：本题主要考查动点问题的函数图象与菱形的性质、解直角三角形的应用，结合函数图象上特殊点的实际意义排除法求解是解此题的关键．
6、D
【解析】
∵0.036>0.035>0.028>0.015,
∴丁最稳定，故选D.
7、D
【解析】
根据两内项之积等于两外项之积对各选项分析判断即可得解
【详解】
解：由得3a=2b,
A. 由可得：3a=2b, 本选项正确；
B. 由可得：3a=2b, 本选项正确；
C. , 可知本选项正确；
D. ,由前面可知本选项错误。
故选：D
本题考查了比例的性质，熟练掌握内项之积等于外项之积是解题的关键．
8、A
【解析】
首先找出考查的对象，从而找出总体、个体，再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量.
【详解】
解：在这个问题中总体是：所有该种新车的100千米耗油量；
样本是：20辆该种新车的100千米耗油量；
样本容量为：20
个体为：每辆该种新车的100千米耗油量；
故选：A.
本题考查了总体、个体、样本、样本容量的定义,解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象.总体、个体与样本的考查对象是相同的，所不同的是范围的大小.样本容量是样本中包含的个体的数目，不能带单位.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、0.4
【解析】
根据计算仰卧起坐次数在次的频率.
【详解】
由图可知：仰卧起坐次数在次的频率.
故答案为：.
此题考查了频率、频数的关系：.
10、1.
【解析】
先将化成最简二次根式，然后根据同类二次根式得到被开方数相同可得出关于a的方程，解出即可．
【详解】
∵与最简二次根式是同类二次根式，且＝1，
∴a+1=3，解得：a=1．
故答案为1．
本题考查了同类二次根式的定义：化成最简二次根式后，被开方数相同，这样的二次根式叫做同类二次根式．
11、8
【解析】
试题分析：根据图形以及等腰直角三角形的性质可得：正方形①的边长为64cm；正方形②的边长为32cm；正方形③的边长为32cm；正方形④的边长为16cm；正方形⑤的边长为16cm；正方形⑥的边长为8cm；正方形⑦的边长为8cm.
考点：等腰直角三角形的性质
12、3
【解析】
先说明OE是△BCD的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半求解．
【详解】
∵▱ABCD的对角线AC、BD相交于点O，
∴OB=OD，AD=BC=6
∵点E是CD的中点，
∴CE=DE，
∴OE是△BCD的中位线，
∵AD=6，
∴OE=AD=3.
故答案为：3
此题考查平行四边形的性质，解题关键在于利用OE是△BCD的中位线
13、2．
【解析】
试题分析：由图可得出两条路的宽度为：1m，长度分别为：10m，30m，这样可以求出小路的总面积，又知矩形的面积，耕地的面积=矩形的面积-小路的面积，由此计算耕地的面积．
由图可以看出两条路的宽度为：1m，长度分别为：10m，30m，
所以，可以得出路的总面积为：10×1+30×1-1×1=49m1，
又知该矩形的面积为：10×30=600m1，
所以，耕地的面积为：600-49=2m1．
故答案为2．
考点：矩形的性质．
三、解答题（本大题共5个小题，共48分）
14、 (1) B(0，6)；(2) d=﹣t+10；(3)见解析.
【解析】
【分析】(1)把A(8，0)代入y=﹣x+b，可求解析式，再求B的坐标；（2）先求点C(0，﹣4)，再求直线AC解析式，可设点P(t，﹣t+6)，Q(t， t﹣4)，所以d=(﹣t+6)﹣(t﹣4)；过点M作MG⊥PQ于G，证△OAC≌△GMQ，得QG=OC=4，GM=OA=8；过点N作NH⊥PQ于H，过点M作MR⊥NH于点R，得四边形GHRM是矩形，得HR=GM=8；设GH=RM=k，由△HNQ≌△RMN，得HN=RM=k，NR=QH=4+k，由HR=HN+NR，得k+4+k=8，可得GH=NH=RM=2，HQ=6，由Q(t，t﹣4)，得N(t+2，t﹣4+6)，代入y=﹣x+6，得t+2=﹣(t+2)+6，求出t=2，再求P(2，)，N(4，3)，可得PH=，NH=2，最后PN=.
【详解】解：(1)∵y=﹣x+b交x轴于点A(8，0)，
∴0=﹣×8+b，b=6，
∴直线AB解析式为y=﹣x+6，令x=0，y=6，B(0，6)；
(2)∵A(8，0)，B(0，6)，
∴OA=8，OB=6，
∵∠AOB=90°，
∴AB=10=BC，
∴OC=4，
∴点C(0，﹣4)，设直线AC解析式为y=kx+b’，
∴，
∴,
∴直线AC解析式为y=x﹣4，
∵P在直线y=﹣x+6上，
∴可设点P(t，﹣t+6)，
∵PQ∥y轴，且点Q在y=x﹣4 上，
∴Q(t， t﹣4)，
∴d=(﹣t+6)﹣(t﹣4)=﹣t+10；
(3)过点M作MG⊥PQ于G，
∴∠QGM=90°=∠COA，
∵PQ∥y轴，
∴∠OCA=∠GQM，
∵CQ=AM，
∴AC=QM，在△OAC与△GMQ中，
，
∴△OAC≌△GMQ，
∴QG=OC=4，GM=OA=8，过点N作NH⊥PQ于H，过点M作MR⊥NH于点R，
∴∠MGH=∠RHG=∠MRH=90°，
∴四边形GHRM是矩形，
∴HR=GM=8，可设GH=RM=k，
∵△MNQ是等腰直角三角形，
∴∠QMN=90°，NQ=NM，
∴∠HNQ+∠HQN=90°，
∴∠HNQ+∠RNM=90°，
∴∠RNM=∠HQN，
∴△HNQ≌△RMN，
∴HN=RM=k，NR=QH=4+k，
∵HR=HN+NR，
∴k+4+k=8，
∴k=2，
∴GH=NH=RM=2，
∴HQ=6，
∵Q(t，t﹣4)，
∴N(t+2，t﹣4+6)即 N(t+2，t+2)
∵N在直线AB：y=﹣x+6上，
∴t+2=﹣(t+2)+6，
∴t=2，
∴P(2，)，N(4，3)，
∴PH=，NH=2，
∴PN=
=.
【点睛】本题考核知识点：一次函数综合应用.解题关键点：熟记一次函数性质，运用数形结合思想.
15、（1）；（2）y=+2
【解析】
（1）由AC=OC，设A（m,m）代入反比例函数得m2=9，求出A点坐标；
（2）利用四边形ABOC的面积求出B点坐标，再用待定系数法确定函数关系式即可求出AB的解析式.
【详解】
（1）∵AC=OC
∴可设A（m,m）
∵点A（m,m）在y=的图像上
∴m2=9
∴m=±3
∵x＞0
∴m=3
（2）∵AC⊥x轴，OB⊥x轴
∴ S四边形ABOC==(3+OB)·3=
∴OB=2
∴B（0，2）
∵y=kx+b过点A（3，3），B（0，2）
∴
∴
∴一次函数的表达式为y=+2
此题主要考查反比例函数钰一次函数综合，解题的关键是求出A点坐标.
16、（1）①BE＝2；②证明见解析；（2）①BE＝2；②S1：S2＝1
【解析】
【分析】（1）①在矩形 ABCD 中，∠B＝∠DCE＝90°，BC＝AD＝5，DC＝AB＝4，由勾股定理求得CE的长，即可求得BE的长；
②证明△CED≌△DEF，可得∠CED＝∠FED，从而可得∠ADE＝∠AED，即可得到AD＝AE；
（2）①分两种情况点 E 在线段 BC 上、点 E 在 BC 延长线上两种情况分别讨论即可得；
②S1：S2＝1，当 BF//DE 时，延长 BF 交 AD 于 G，由已知可得到四边形 BEDG 是平行四边形，继而可得S△DEF＝S平行四边形 BEDG，S △BEF＋S△ DFG＝ S平行四边形 BEDG，S△ABG＝S△CDE，根据面积的知差即可求得结论.
【详解】（1）①在矩形 ABCD 中，∠B＝∠DCE＝90°，
BC＝AD＝5，DC＝AB＝4，
∵DE＝5，
∴CE＝=3，
∴BE＝BC-CE=5-3=2；
②在矩形 ABCD 中，∠DCE＝90°，AD//BC，
∴∠ADE＝∠DEC，∠DCE＝∠DFE，
∵CE＝EF，DE＝DE，
∴△CED≌△DEF（HL），
∴∠CED＝∠FED，
∴∠ADE＝∠AED，
∴AD＝AE；
（2）①当点 E 在线段 BC 上时，AF＝BF，如图所示：
∴∠ABF＝∠BAF，
∵∠ABF＋∠EBF＝90°，
∠BAF＋∠BEF＝90°，
∴∠EBF＝∠BEF，
∴EF＝BF ，∴AF＝EF，
∵DF⊥AE，
∴DE＝AD＝5，
在矩形 ABCD 中，CD＝AB＝4，∠DCE＝90°，
∴CE＝3，
∴BE＝5－3＝2；
当点 E 在 BC 延长线上时，AF＝BF，如图所示，
同理可证 AF＝EF，
∵DF⊥AE，
∴DE＝AD＝5，
在矩形 ABCD 中，CD＝AB＝4，∠DCE＝90°，
∴CE＝3，
∴BE＝5＋3＝8，
综上所述，可知BE=2或8；
②S1：S2＝1，解答参考如下：
当 BF//DE 时，延长 BF 交 AD 于 G，
在矩形 ABCD 中，AD//BC，AD＝BC，AB＝CD，
∠BAG＝∠DCE＝90°，
∵BF//DE，
∴四边形 BEDG 是平行四边形，
∴BE＝DG，S△DEF＝S平行四边形 BEDG，
∴AG＝CE，S △BEF＋S△ DFG＝ S平行四边形 BEDG，
∴△ABG≌△CDE，
∴S△ABG＝S△CDE，
∵S △ABE＝ S平行四边形 BEDG，
∴S△ABE＝S△BEF＋S△DFG，
∴S△ABF＝S△DFG，
∴S△ABF＋S△AFG＝S△DFG＋S△AFG即 S△ABG＝S△ADF，
∴S△CDE＝S△ADF，即 S1：S2＝1.
【点睛】本题考查了矩形的性质、全等三角形的判定与性质、勾股定理等，综合性较强，有一定的难度，熟练掌握和灵活用相关知识是解题的关键.
17、 (1) ﹣4≤y＜1；（2）点P的坐标为（2，﹣2） .
【解析】
利用待定系数法求一次函数解析式得出即可；
（1）利用一次函数增减性得出即可．
（2）根据题意得出n=﹣2m+2，联立方程，解方程即可求得．
【详解】
设解析式为：y=kx+b，
将（1，0），（0，2）代入得：，
解得：，
∴这个函数的解析式为：y=﹣2x+2；
（1）把x=﹣2代入y=﹣2x+2得，y=1，
把x=3代入y=﹣2x+2得，y=﹣4，
∴y的取值范围是﹣4≤y＜1．
（2）∵点P（m，n）在该函数的图象上，
∴n=﹣2m+2，
∵m﹣n=4，
∴m﹣（﹣2m+2）=4，
解得m=2，n=﹣2，
∴点P的坐标为（2，﹣2）．
考点：1、待定系数法求一次函数的解析式，2、一次函数图象上点的坐标特征，3、一次函数的性质
18、 (1)证明见解析；(2)12.
【解析】
（1）根据题意得到且，可得四边形ACDE为平行四边形；
（2）先证四边形ACDE为菱形，然后根据菱形的面积公式计算即可.
【详解】
解：(1)在中，，．
，
∵，．
四边形ACDE为平行四边形．
(2)∵，，
．
四边形ACDE为菱形．
∵，，
．
本题考查了平行四边形和菱形的判定和性质，能够熟练应用基础知识进行推理是解题关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、-3
【解析】
点P（m+2，2m+1）向右平移1个单位长度后 ，正好落在y轴上，则
20、
【解析】
根据新定义列出不等式即可求解.
【详解】
依题意得-3x+5≤11
解得
故答案为：.
此题主要考查列不等式，解题的关键是根据题意列出不等式进行求解.
21、小于
【解析】
先分别求出摸出各种颜色球的概率，再进行比较即可得出答案．
【详解】
解：∵袋子中有1个白球、1个红球和2个黄球，共有4个球，
∴摸到白球的概率是，摸到红球的概率是，摸到黄球的概率是=，
∴摸出白球可能性＜摸出黄球的可能性；
故答案为小于．
本题主要考查了可能性的大小，用到的知识点为：可能性等于所求情况数与总情况数之比．
22、x≤1
【解析】
分析：根据二次根式有意义的条件解答即可.
详解：
∵二次根式有意义，被开方数为非负数，
∴1 -x≥0，
解得x≤1.
故答案为x≤1.
点睛：本题考查了二次根式有意义的条件，熟知二次根式有意义，被开方数为非负数是解题的关键.
23、
【解析】
通过四边形ABCD是矩形以及，得到△FEM是等边三角形，根据含30°直角三角形的性质以及勾股定理得到KM，NK，KE的值，进而得到NE的值，再利用30°直角三角形的性质及勾股定理得到BN，BE即可．
【详解】
解：如图，设NE交AD于点K，
∵四边形ABCD是矩形，
∴AD∥BC，∠ABC=90°，
∴∠MFE=∠FCB，∠FME=∠EBC
∵，
∴△BCE为等边三角形，
∴∠BEC=∠ECB=∠EBC=60°，
∵∠FEM=∠BEC，
∴∠FEM=∠MFE=∠FME=60°，
∴△FEM是等边三角形，FM=FE=EM=2，
∵EN⊥BE，
∴∠NEM=∠NEB=90°，
∴∠NKA=∠MKE=30°，
∴KM=2EM=4，NK=2AN=6，
∴在Rt△KME中，KE=，
∴NE=NK+KE=6+，
∵∠ABC=90°，
∴∠ABE=30°，
∴BN=2NE=12+，
∴BE=，
∴BC=BE=，
故答案为：
本题考查了矩形，等边三角形的性质，以及含30°直角三角形的性质与勾股定理的应用，解题的关键是灵活运用30°直角三角形的性质．
二、解答题（本大题共3个小题，共30分）
24、（1）（0，1）；（2）①k=；②N（-3，）；③直线 l2的解析式为y=x+1．
【解析】
（1）令，求出相应的y值，即可得到A的坐标；
（2）①先设出P的坐标，然后通过点的平移规律得出平移后 的坐标，然后将代入 中即可求出k的值；
②作AB的中垂线与y轴交于M点，连结BM，分别作AM，BM的平行线，相交于点N，则四边形AMBN是菱形, 设M（0，t），然后利用勾股定理求出t的值，从而求出OM的长度，然后利用BN=AM求出BN的长度，即可得到N的坐标；
③先根据题意画出图形，过点B作BC⊥l1，交l2于点C，过点C作CD⊥x轴于D，利用等腰三角形的性质和AAS证明△AOB≌△BDC，得出AO=BD，OB=DC，进一步求出点C的坐标，然后利用待定系数法即可求出直线l2的解析式．
【详解】
（1）∵y=kx+1与y轴交于点A，
令， ，
∴A（0，1）．
（2）①由题意得：P（m，km+1），
∵将点P向左平移3个单位，再向下平移1个单位，得点P′，
∴P′（m-3，km），
∵P′（m-3，km）在射线AB上，
∴k（m-3）+1=km，
解得：k=．
②如图，作AB的中垂线与y轴交于M点，连结BM，过点B作AM的平行线，过点A作BM的平行线，两平行线相交于点N，则四边形AMBN是菱形．
，
，
当 时，，解得 ，
∴ ．
设M（0，t），则AM=BM=1-t，
在Rt△BOM中，OB2+OM2=BM2，
即32+t2=（1-t）2，
解得：t=，
∴M（0，），
∴OM=，BN=AM=1-=，
∴N（-3，）．
③如图，过点B作BC⊥l1，交l2于点C，过点C作CD⊥x轴于D．则∠ABC=∠BDC=90°，

∵∠BAC=15°，
∴△ABC是等腰直角三角形，
∴AB=BC，∠ABO+∠CBD=90°，
又∵∠ABO+∠BAO=90°，
∴∠BAO=∠CBD，
在和中，
∴△AOB≌△BDC（AAS），
∴AO=BD=1，OB=DC=3，
∴OD=OB+BD=3+1=7，
∴C（-7，3），
设直线 l2的解析式为：y=ax+1，
则-7a+1=3，
解得：a=．
∴直线 l2的解析式为：y=x+1．
本题主要考查全等三角形的判定及性质，菱形的性质，勾股定理，一次函数与几何综合，解题的关键在于合理的添加辅助线，构造出全等三角形．
25、（1）；（2）塔的顶层共有3盏灯；（3）18或95
【解析】
（1）根据材料的方法可设S=1+3+9+27+…+3n．则3S=3（1+3+9+27+…+3n），利用即可解答．
（2）设塔的顶层由x盏灯，根据一座7层塔共挂了381盏灯，可列方程．根据材料的结论即可解答．
（3）由题意求得数列的分n+1组，及前n组和S=2n+1-2-n，及项数为，由题意可知：2n+1为2的整数幂．只需最后一组将-2-n消去即可，求出n值即可求得N的值
【详解】
解：（1）设S=1+3+9+27+…+3n，则3S=3（1+3+9+27+…+3n）=3+9+27+…+3n+3n+1，
∴3S-S=（3+9+27+…+3n+3n+1）-（1+3+9+27+…+3n），
∴2S=3n+1-1，
（2）设塔的顶层由x盏灯，依题意得：
x+21x+22x+23x+24x+25x+26x=381
解得：x=3，
答：塔的顶层共有3盏灯．
（3）由题意这列数分n+1组：前n组含有的项数分别为：1，2，3，…，n，最后一组x项，根据材料可知每组和公式，求得前n组每组的和分别为：21-1，22-1，23-1，…，2n-1，
总前n组共有项数为N=1+2+3+…+n=
前n所有项数的和为Sn=21-1+22-1+23-1+…+2n-1=（21+22+23+…+2n）-n=2n+1-2-n，
由题意可知：2n+1为2的整数幂．只需最后一组x项将-2-n消去即可，
则①1+2+（-2-n）=0，解得：n=1，总项数为，不满足10＜N＜100，
②1+2+4+（-2-n）=0，解得：n=5，总项数为，满足10＜N＜100，
③1+2+4+8+（-2-n）=0，解得：n=13，总项数为，满足10＜N＜100，
④1+2+4+8+16+（-2-n）=0，解得：n=29，总项数为，不满足10＜N＜100，
∴所有满足条件的软件激活码正整数N的值为：18或95。
本题考查了有理数的乘方，读懂题目信息，理解等比数列的求和方法是解题的关键．
26、（1），，；（2）
【解析】
（1）将点（3，0）和点P的坐标代入一次函数的解析式求得m、b的值，然后将点P的坐标代入正比例函数解析式即可求得a的值；
（2）直接根据函数的图象结合点P的坐标确定不等式的解集即可．
【详解】
（1）∵正比例函数与过点的一次函数交于点．
∴
∴
∴
∴
∴
∴
∴
（2）直接根据函数的图象，可得不等式的解集为：
本题考查了求一次函数解析式，一次函数与一元一次不等式的问题，解题的关键是能够确定有关待定系数的值，难度不大．
题号
一
二
三
四
五
总分
得分
选手
甲
乙
丙
丁
方差
0.035
0.036
0.028
0.015