数学1.2 二次根式的性质教案及反思

这是一份数学1.2 二次根式的性质教案及反思，共3页。


课题
1.2.1 二次根式的性质
单元
1
学科
数学
年级
八
学习
目标
1.经历二次根式的性质的发现过程，体验归纳、猜想的思想方法；
2.了解二次根式的上述两个性质；
3.会运用上述两个性质进行有关计算。
重点
理解二次根式的上述两个性质
难点
灵活运用上述两个性质进行 有关计算。
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
1.什么是二次根式？
2.二次根式被开方数满足的条件
学生思考回答
回顾上节内容，为后面的学习奠定基础
讲授新课
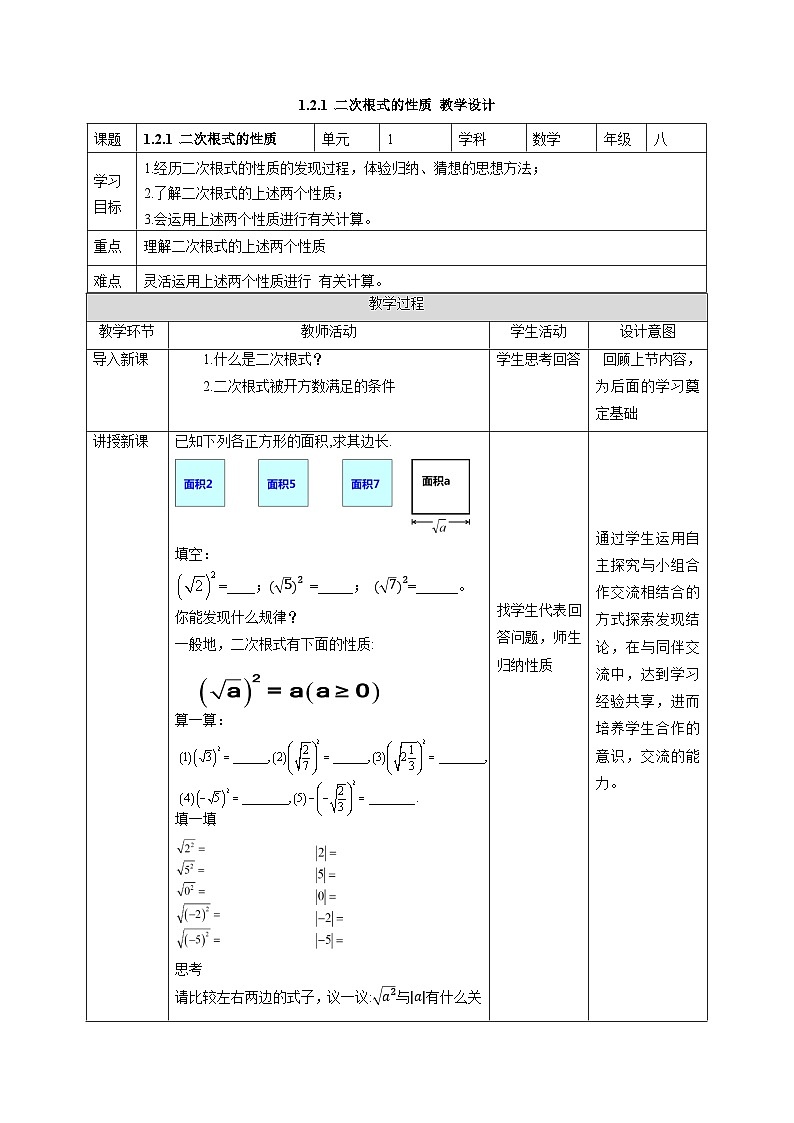
已知下列各正方形的面积,求其边长.
填空：
=____；(5)2 =_____； (7)2=______。
你能发现什么规律？
一般地，二次根式有下面的性质:
算一算：
填一填

思考
请比较左右两边的式子，议一议:a2与a有什么关系？
当a≥0时，a2＝______;当a<0，a2＝_______ .
总结归纳：
总结规律：（1）从运算顺序来看,
先开方,后平方；
先平方,后开方；
（2）从取值范围来看，
a≥0
a取任何实数
（3）从运算结果来看，
（a）2=a
a2=aa(a≥0)-a(a<0)
例1 计算
（1）
（2）
例题2：计算
找学生代表回答问题，师生归纳性质
自主探究后小组讨论
观察
思考
练习
部分学生板演
通过学生运用自主探究与小组合作交流相结合的方式探索发现结论，在与同伴交流中，达到学习经验共享，进而培养学生合作的意识，交流的能力。
采用学生先自主探究，然后小组交流，从而得出a2的结果，通过自己解答，发现规律，提高学生自主探索的能力
运用二次根式的两个性质解决基础的运算问题
课堂练习
1.化简16得（ ）
A. ±4 B. ±2 C. 4 D.-4
2. 当1A.3 B.-3 C.1 D.-1
3.化简：
（1）9＝ ; （2）（-4）2＝ ;
（3）（-7）2 = ; （4）（81）2= .
4. 实数a在数轴上的位置如图所示，化简a-2+(a-1)2的结果是___ .
5.实数a、b在数轴上的对应点如图所示，请你化简:a2-b2+(a-b)2
6.已知a、b、c是△ABC的三边长，化简：(a+b+c)2-b+c-a2+(c-b-a)2
7.（2020•苏州）若式子(2-x)2+(x-4)2的值是常数2，则x的取值范围是( )
A．x≥4
B．x≤2
C．2≤x≤4
D．x=2或x=4
学生自主解答，老师订正答案
巩固和运用二次根式的两个性质
课堂小结
二次根式的两个性质
性质一：
性质二：
学生自由回答
梳理和巩固知识
板书
1.2二次根式的性质（1）

性质一：
性质二：
例1 （1） （2）
例2