数学八年级下册1.2 二次根式的性质教案设计

目标明确

价值导向

真、仁、义、礼、慧、信、德、俭、美、善、勤、爱、公、法、敬、诚、净、和、廉、荣、耻、谦、勇、精、学、用。

学习技能

听、说、阅、记、合、练、疑、问、理、思

课堂知识

基础

1、我能通过二次根式乘除法的归纳类比，得到二次根式的乘法、除法性质

提升

1、     我能运用二次根式的性质将二次根式化为最简

2、     我能合理应用二次根式的性质简化实数的运算

挑战

1、     我能通过利用二次根式的乘除法的性质，对含参的二次根式进行化简

路径清晰

问题巧妙

路径清晰

问题巧妙

路径清晰

问题巧妙

教 学 流 程 模 块 设 计

反 馈

反思

目标

方式

时间

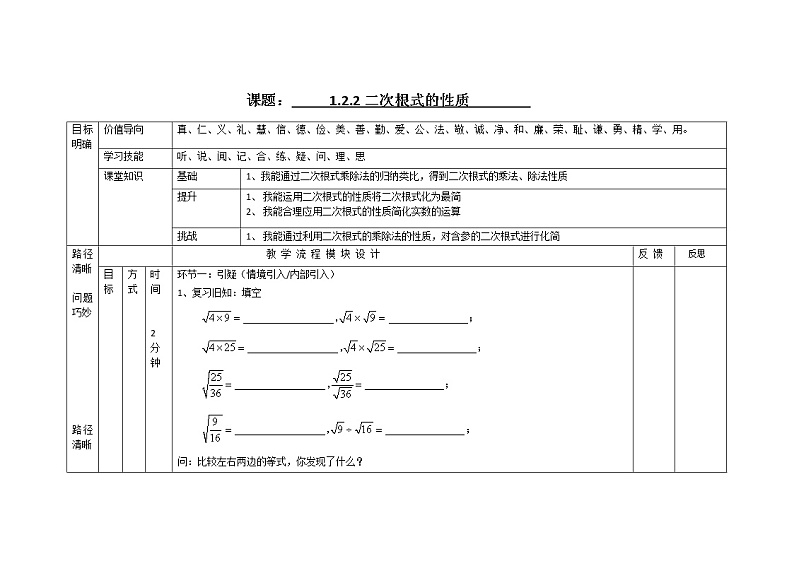
2

分钟

环节一：引疑（情境引入/内部引入）

1、复习旧知：填空

[来源:学&科&网Z&X&X&K]

问：比较左右两边的等式，你发现了什么？

追问：你能用字母表示你发现的规律吗？

目标

提升1

方式

合作探究

合作探究

时间

5分钟

环节二：探索新知（操作观察）

归纳；

1、积的算术平方根的性质。

积的算术平方根，等于积中各因式的算术平方根的积（各因式必须是非负数）  即

2、商的算术平方根的性质。

商的算术平方根等于被除式的算术平方根除以除式的算术平方根（被除式必须是非负数，除式必须是正数）。

即

问：你能运用上述性质出一些代数式来让同学们帮你化简吗？

环节三：应用新知（应用举例）

例1、化简：

强调：一般地，二次根式化简的结果应使根号内的数是一个自然数，且在该自然数的因数中，不含有1以外的自然数的平方数。

像这样，在根号内不含分母，不含开得尽方的因数或因式，这样的二次根式我们就说它是最简二次根式。[来源:Zxxk.Com]

例2、化简：

环节四：分层演练（A/B）

A层

1、判断下列等式是否成立？若不成立，请说明理由并改正：

（1）=×；

（2）   ==2（a为任意实数）

2、化简：⑴； ⑵   ； ⑶.

3．-=________．

4、

5、补充练习若b>0，x<0，化简：

B层

1、判断下列等式是否成立？若不成立，请说明理由并改正：

（1）=×；

（2）   ==2（a为任意实数）

2、化简：⑴； ⑵   ； ⑶.

3．-=________．

4、

环节五：梳理小结

说出本节课自己的感悟和收获.

1、二次根式的性质：

2、积的性质：=· (a≥0,b≥0);

3、商的性质：  = （ a≥0,b＞0）

练习

︵训练︶设计

目

标

5分

环节六：目标检测

素养小测

反 馈

反  思

知识结构

（板书）

1.2.2二次根式的性质