数学必修 第二册8.2 立体图形的直观图同步练习题
展开
这是一份数学必修 第二册8.2 立体图形的直观图同步练习题,共8页。试卷主要包含了下列说法中正确的是等内容,欢迎下载使用。
1.(多选)用斜二测画法画水平放置的平面图形的直观图,对其中的线段说法正确的是( )
A.原来相交的仍相交 B.原来垂直的仍垂直
C.原来平行的仍平行 D.原来共点的仍共点
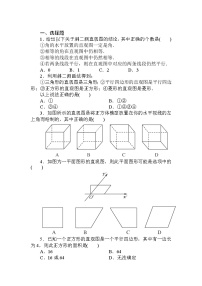
2.下列直观图是将正方体模型放置在你的水平视线的左下角而绘制的是( )
由几何体直观图的画法及直观图中虚线的使用,可知A符合题意.
3.下列说法中正确的是( )
A.相等的角在直观图中对应的角仍然相等
B.相等的线段在直观图中对应的线段仍然相等
C.不相等的线段在直观图中对应的线段一定不相等
D.线段的中点在直观图中仍然是线段的中点
4.(多选)已知水平放置的正方形一条边在x轴上,其由斜二测画法得到的直观图是一个平行四边形,其中有一个边长为4,则此正方形的面积可以为( )
A.16 B.64
C.32 D.无法确定
5.由斜二测画法得到的水平放置的△ABC的直观图△A′B′C′如图所示,其中B′O′=C′O′=1,A′O′=eq \f(\r(3),2),那么△ABC是一个( )
A.等边三角形
B.直角三角形
C.三边中只有两边相等的等腰三角形
D.三边互不相等的三角形
6.如图所示,梯形A′B′C′D′是用斜二测画法得到的水平放置的平面图形ABCD的直观图,A′D′=2B′C′=2,A′B′=1,则平面图形ABCD的面积为( )
A.2 B.2eq \r(2) C.3 D.3eq \r(2)
7.由斜二测画法得到的水平放置的△ABC的直观图如图所示,已知A′C′=2,B′C′=eq \f(3,2),则边AB上的中线的实际长度为________.
8.如图,已知由斜二测画法得到的水平放置的四边形ABCD的直观图是一个边长为1的正方形,则原图形的面积为______.
9.用斜二测画法画出图中水平放置的四边形OABC的直观图.
10.如图,由斜二测画法得到的一个水平放置的平面图形的直观图是一个底角为45°,腰和上底均为1的等腰梯形,求原图形的面积.
11.如图是用斜二测画法得到的水平放置的Rt△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过点A′作A′C′⊥x′轴于点C′,则A′C′的长为( )
A.2eq \r(2) B.eq \r(2) C.16eq \r(2) D.1
12.(多选)如图是由斜二测画法得到的水平放置的△ABC的直观图△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,则由图形可知下列结论中正确的是( )
A.AB=BC=AC B.AD⊥BC
C.AB⊥BC D.AC>AD>AB>BC
13.由斜二测画法得到的一个水平放置的三角形的直观图是等腰三角形,底角为30°,腰长为2,如图,那么它在原平面图形中,顶点B到x轴的距离是( )
A.1 B.2 C.eq \r(2) D.2eq \r(2)
14.一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面重合,已知长方体的长、宽、高分别为20 m,5 m,10 m,四棱锥的高为8 m,若利用斜二测画法按1∶500的比例画出它的直观图,那么直观图中长方体的长为________ cm,宽为________ cm,建筑物的高为________ cm.
15.如图所示,△A′O′B′表示由斜二测画法得到的水平放置的△AOB的直观图,B′在x′轴上,A′O′与x′轴垂直,且A′O′=2,则△AOB的边OB上的高为( )
A.2 B.4 C.2eq \r(2) D.4eq \r(2)
16.现欲设计一个大屋,该大屋可近似地看作一个直四棱柱和一个三棱柱的组合体,请画出其直观图(尺寸自定).
§8.2 立体图形的直观图
1.ACD 2.A 3.D 4.AB 5.A
6.C 7.eq \f(\r(13),2) 8.2eq \r(2)
9.解 (1)画x′轴、y′轴,两轴相交于点O′,使∠x′O′y′=45°.
(2)在x′轴上取点H,使O′H=3,作HA′∥y′轴,并取A′H=1(A′在x′轴下方),在y′轴正半轴上取点C′,使O′C′=1.
在x′轴正半轴上取点B′,使O′B′=4,顺次连接O′,A′,B′,C′,如图①所示.
(3)擦去作为辅助线的坐标轴、线段A′H、点H,便得到四边形OABC的直观图O′A′B′C′,如图②所示.
10.解 因为该直观图是一个底角为45°,腰和上底均为1的等腰梯形,所以原图形ABCD为直角梯形,且AB⊥BC,且AB=2A′B′=2,AD=A′D′=1,又在等腰梯形A′B′C′D′中,
B′C′=1+2×eq \f(\r(2),2)=1+eq \r(2),
所以BC=B′C′=1+eq \r(2),
所以S梯形ABCD=eq \f(1,2)(AD+BC)·AB=eq \f(1,2)×(1+1+eq \r(2))×2=2+eq \r(2),所以原图形的面积为2+eq \r(2).
11.A 12.CD
13.D [过点B′作B′C′∥y′轴,交x′轴于点C′,如图,
在△O′B′C′中,∠B′O′C′=30°,∠B′C′O′=135°,O′B′=2,由正弦定理得eq \f(B′C′,sin 30°)=eq \f(O′B′,sin 135°),
于是得B′C′=eq \f(2×\f(1,2),\f(\r(2),2))=eq \r(2),
由斜二测画法规则知,在原平面图形中,顶点B到x轴的距离是2eq \r(2).]
14.4 0.5 3.6
解析 由比例可知长方体的长、宽、高分别为4 cm,1 cm,2 cm,四棱锥的高为1.6 cm,
所以长方体的直观图的长、宽、高应分别为4 cm,0.5 cm,2 cm,四棱锥的直观图的高为
1.6 cm.
所以直观图中建筑物的高为2+1.6=3.6(cm).
15.D [设△AOB的边OB上的高为h,因为S原图形=2eq \r(2)S直观图,所以eq \f(1,2)×OB×h=2eq \r(2)×eq \f(1,2)×2×O′B′.
又OB=O′B′,所以h=4eq \r(2).]
16.解 (1)先按照斜二测画法画出直四棱柱的直观图A′B′C′D′-ABCD如图1.
(2)以直四棱柱的上底面ABCD为三棱柱的一个侧面画出三棱柱的直观图ADE-BCF.
直观图如图2所示.
相关试卷
这是一份人教A版 (2019)必修 第二册8.2 立体图形的直观图课时训练,共36页。
这是一份必修 第二册8.2 立体图形的直观图同步练习题,共6页。试卷主要包含了故选D等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.4 空间点、直线、平面之间的位置关系一课一练,共9页。试卷主要包含了D 2,A1B1 AC 8,证明 如图,∵AC∥BD,,C [等内容,欢迎下载使用。