资料中包含下列文件,点击文件名可预览资料内容








还剩52页未读,
继续阅读
成套系列资料,整套一键下载
人教版数学八年级下册 第十八章《四边形》章节复习课件+章节教学设计+章节复习导学案+单元测试卷(含答案解析)
展开
这是一份人教版数学八年级下册 第十八章《四边形》章节复习课件+章节教学设计+章节复习导学案+单元测试卷(含答案解析),文件包含人教版数学八年级下册第十八章《四边形》章节复习课件pptx、人教版数学八年级下册第十八章《四边形》章节教学设计docx、人教版数学八年级下册第十八章《四边形》章节复习导学案docx等3份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
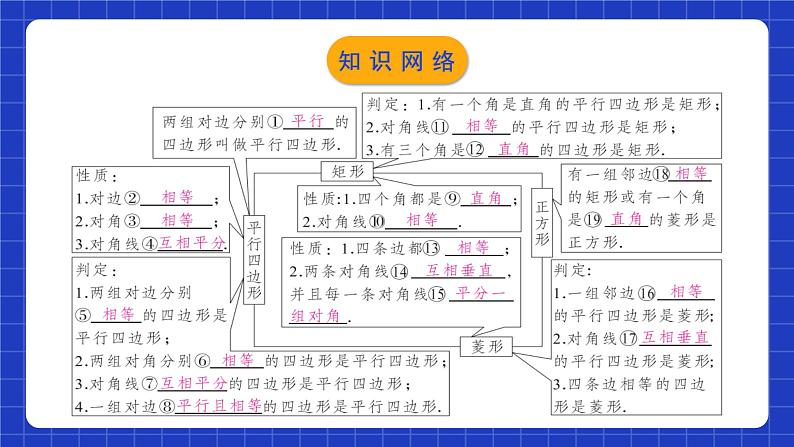
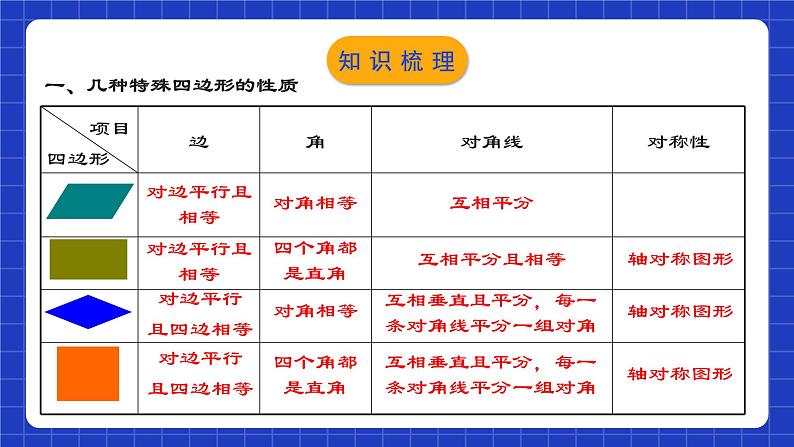
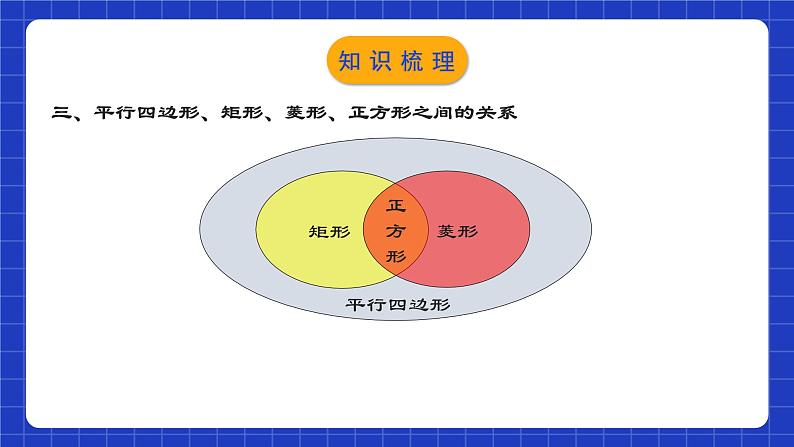
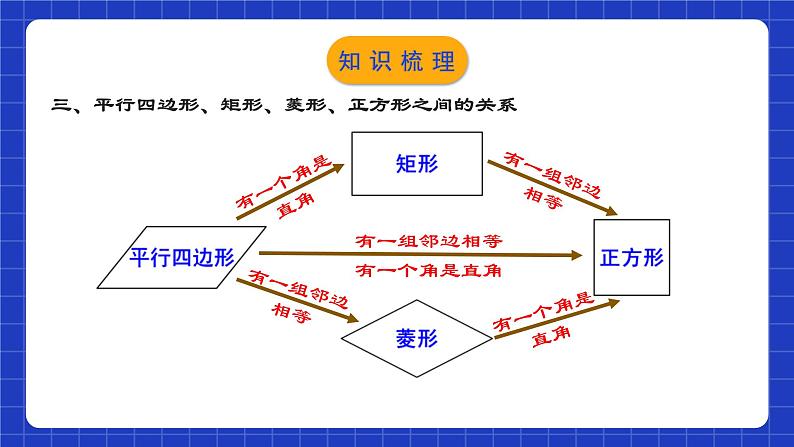
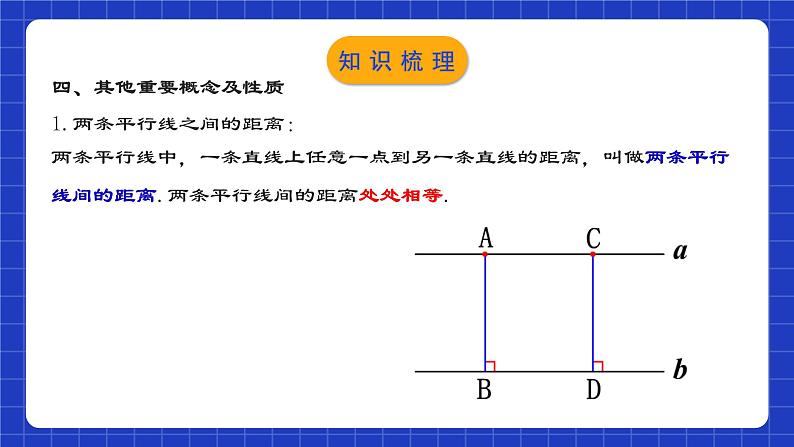
四边形章节复习学习目标0102031.进一步理清平行四边形(特殊四边形)之间的联系与区别; (重点)2.对本章知识结构、知识要点进行复习梳理; (重点)3.分考点归纳常见题型的解题方法与策略. (难点)知识网络一、几种特殊四边形的性质对边平行且相等对边平行且相等对边平行且四边相等对边平行且四边相等对角相等四个角都是直角对角相等四个角都是直角互相平分互相平分且相等轴对称图形轴对称图形轴对称图形互相垂直且平分,每一条对角线平分一组对角互相垂直且平分,每一条对角线平分一组对角知识梳理二、几种特殊四边形的常用判定方法:1.定义:两组对边分别平行;2.两组对边分别相等;3.两组对角分别相等; 4.对角线互相平分; 5.一组对边平行且相等. 1.定义:有一个角是直角的平行四边形; 2.对角线相等的平行四边形; 3.有三个角是直角的四边形.1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形; 3.四条边都相等的四边形.1.定义:一组邻边相等且有一个角是直角的平行四边形;2.有一组邻边相等的矩形; 3.有一个角是直角的菱形.知识梳理三、平行四边形、矩形、菱形、正方形之间的关系 矩形 菱形正方形平行四边形知识梳理三、平行四边形、矩形、菱形、正方形之间的关系有一组邻边相等有一个角是直角有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等知识梳理四、其他重要概念及性质1.两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线间的距离.两条平行线间的距离处处相等.知识梳理四、其他重要概念及性质2.三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. 知识梳理四、其他重要概念及性质3.直角三角形斜边上的中线:直角三角形斜边上的中线等于斜边的一半. 知识梳理考点梳理01平行四边形的性质与判定例1.如图,点B,E分别在AC,DF上,AF分别交BD,CE于点M,N,∠A=∠F,∠1=∠2.(1)求证:四边形BCED是平行四边形;证明:∵∠A=∠F,∴DE∥BC.∵∠1=∠2,且∠1=∠DMF,∴∠DMF=∠2.∴DB∥EC.∴四边形BCED为平行四边形.考点解析(2)已知DE=2,连接BN.若BN平分∠DBC,求CN的长.解:∵BN平分∠DBC,∴∠DBN=∠CBN.∵EC∥DB,∴∠CNB=∠DBN.∴∠CNB=∠CBN.∴CN=BC.由(1)可知四边形BCED是平行四边形.∴BC=DE=2.∴CN=2.考点解析 C考点解析 CB迁移应用【1-3】如图,在□ABCD中,BN=DM,BE=DF,求证:四边形MENF是平行四边形.证明:∵四边形ABCD是平行四边形∴BC//AD∴∠EBN= ∠FDM∵BN=DM,BE=DF∴△EBN≌△FDM (SAS)∴EN=FM,∠BEN= ∠DFM∴∠FEN=∠EFM∴EN// FM∴四边形MENF是平行四边形迁移应用【1-4】如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.(1)求证:四边形AECD是平行四边形;证明:∵∠ACB=∠CAD=90°,∴AD∥CE.∵AE∥DC,∴四边形AECD是平行四边形.迁移应用(2)若AE平分∠BAC,BE=5,BF=4,求AD的长. 迁移应用02三角形的中位线的应用例3.如图,在△ABC中,点M,N分别是AB,AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,求CD的长. 考点解析证明:取AC的中点F,连接BF.∵BD=AB,∴BF为△ADC的中位线,∴DC=2BF.∵E为AB的中点,AB=AC,∴BE=CF,∠ABC=∠ACB.∵BC=CB,∴△EBC≌△FCB,∴CE=BF,∴CD=2CE.F例4.如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.考点解析例5.如图,在Rt△ABC中,∠BAC=90°,点E,F分别是BC,AC的中点,延长BA到点D,使得AB=2AD,连接DE,DF,AE,EF,AF与DE相交于点O.(1)求证:AF与DE互相平分;证明:∵点E,F分别是BC,AC的中点,∴EF∥AB,AB=2EF.∵AB=2AD,点D是BA延长线上的一点,∴AD=EF,AD∥EF.∴四边形ADFE是平行四边形.∴AF与DE互相平分.考点解析(2)如果AB=6,BC=10,求DO的长. 考点解析【2-1】如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数. 迁移应用【2-2】如图,E、F、G、H分别为四边形ABCD四边之中点.求证:四边形EFGH为平行四边形. 迁移应用【2-3】如图,在△ABC中,M是BC的中点,AN⊥BN于N点,AN平分∠BAC, 且AB=12, AC=16, 求MN的长. 迁移应用03矩形的性质与判定例6.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数. 考点解析例7.如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.证明:连接DE.∵AD =AE,∴∠AED =∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC, ∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.又∵DE=DE,∴△DFE≌△DCE,∴DF=DC.考点解析例8.在矩形ABCD中,AB=4,BC=3.若点P是CD上任意一点,如图①,PE⊥BD于点E,PF⊥AC于点F.(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系 (3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.考点解析(1)猜想PE和PF之间有怎样的数量关系?写出你的理由. 考点解析(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系; 考点解析(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程. 考点解析 迁移应用【3-2】如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.(1)若AB=4,BC=3,求AE的长. 迁移应用【3-2】如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.(2)连接DF,若点D,F,E在同一条直线上,且DF=2,求AE的长. 迁移应用 迁移应用 迁移应用 迁移应用 04直角三角形斜边中线性质考点解析【4-1】如图,在Rt△ABC中,∠ACB=90°, 点D、E、F分别是边AB、BC、CA的中点.若CD+EF=8,则CD的长为______.4迁移应用【4-2】如图,在□ABCD中,E、F、G分别为AD、OB、OC的中点,且2AB=AC, 求证: EF=GF.证明:连接AF.∵四边形ABCD是平行四边形.∴AD=BC,AC=2AO∵2AB=AC, ∴AB=AO∵F是OB的中点,∴AF⊥OB迁移应用【4-2】如图,在□ABCD中,E、F、G分别为AD、OB、OC的中点,且2AB=AC, 求证: EF=GF. 迁移应用05菱形的性质与判定例10.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.证明:∵四边形ABCD为菱形,∴AD∥BC,AD=BA, ∠ABC=∠ADC=2∠ADB ,∴∠DAE=∠AEB,∵AB=AE,∴∠ABC=∠AEB, ∴∠ABC=∠DAE, ∵∠DAE=2∠BAE,∴∠BAE=∠ADB. 又∵AD=BA ,∴△AOD≌△BEA ,∴AO=BE .考点解析 考点解析(1)求证:四边形EBFD为菱形; 考点解析 考点解析【5-1】如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判定□ ADCE是菱形的是( )A.∠BAC=90° B.∠DAE=90° C. AB=AC D. AB=AEA迁移应用 A迁移应用【5-3】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.证明:∵四边形ABCD是菱形∴AC⊥BD,AB // CD,OB=OD∴∠DCO+∠CDO=90°,∠CDO=∠HBO∵DH⊥AB∴OH是Rt△BDH斜边BD上的中线∴OH=OB∴∠OHB=∠HBO ∴∠OHB=∠CDO∵∠DHO+∠OHB=90° ∴∠DHO=∠DCO迁移应用【5-4】如图,四边形ABCD是菱形,∠BAD=60°, 点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,点F在AD的延长线上,CF⊥AD.(1)求证:四边形CEHF是菱形; 迁移应用(2)若四边形CEHF的面积为18,求菱形ABCD的面积. 迁移应用06正方形的性质与判定例12.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.解:连接PC,AC.∵四边形ABCD是正方形,∴∠FCE=90°, AC垂直平分BD,∴AP=PC.又∵PE⊥BC ,PF⊥DC,∴四边形PECF是矩形,∴PC=EF.∴AP=EF.考点解析例13.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.(1)求证:BF=DE;(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.(1)证明:∵正方形ABCD,∴AB=AD,∠BAD=90°,∵AF⊥AC,∴∠EAF=90°,∴∠BAF=∠EAD,在△ADE和△ABF中,AD=AB ,∠DAE=∠BAF ,AE=AF ,∴△ADE≌△ABF(SAS),∴BF=DE;考点解析 考点解析【6-1】如图,正方形ABCD的两条对角线AC,BD交于点O,点E在BD上,且BE=CD, 则∠BEC的度数为_________.【6-2】如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.67.5° 迁移应用【6-3】如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连接AF、BD,延长BD交AF于H.求证: BH⊥AF.证明:∵四边形AEDC和BCFG是正方形∴AC=DC,CF=CB, ∠ACF=∠BCF=90°∴△ACF≌△DCB (SAS)∴∠AFC=∠DBC又∵∠AFC+∠CAF=90°∴∠DBC+ ∠CAF=90°∴∠AHB=90° 即 BH⊥AF迁移应用【6-4】如图,在正方形ABCD中,Q在CD上,且DQ=CQ,P在BC上,AP=CD+CP,求证: AQ平分∠DAP.证明:延长AQ交BC延长线与E.∵四边形ABCD是正方形∴AD=CD,AD// BC∵∠D=∠QCE,∠DAQ=∠E又∵DQ=CQ∴△ADQ≌△ECQ (AAS)∴AD=CE迁移应用【6-4】如图,在正方形ABCD中,Q在CD上,且DQ=CQ,P在BC上,AP=CD+CP,求证: AQ平分∠DAP.∴CD=CE∴AP=CD+CP=CE+CP=EP∴∠PAQ=∠E∴∠PAQ=∠DAQ,即AQ平分∠DAP迁移应用07中点四边形问题例14.如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE.连接AC,BD.(1)试说明四边形EFGH为平行四边形; 考点解析(2)当AC与BD满足_________时,四边形EFGH是菱形,并证明你的结论; AC=BD考点解析(3)当AC与BD满足__________时,四边形EFGH是矩形;当AC与BD满足__________________ 时,四边形EFGH是正方形(不用证明).AC⊥BD AC⊥BD且AC=BD 考点解析08特殊平行四边形中的定值、最值问题例15.如图,正方形ABCD的边长为4,点E在边AB上,AE=1.若点P为对角线BD上的一个动点,则△PAE周长的最小值是( )A.3 B.4 C.5 D.6D考点解析 提示:分别过点P、点M作BC边的垂线. 考点解析课程结束
四边形章节复习学习目标0102031.进一步理清平行四边形(特殊四边形)之间的联系与区别; (重点)2.对本章知识结构、知识要点进行复习梳理; (重点)3.分考点归纳常见题型的解题方法与策略. (难点)知识网络一、几种特殊四边形的性质对边平行且相等对边平行且相等对边平行且四边相等对边平行且四边相等对角相等四个角都是直角对角相等四个角都是直角互相平分互相平分且相等轴对称图形轴对称图形轴对称图形互相垂直且平分,每一条对角线平分一组对角互相垂直且平分,每一条对角线平分一组对角知识梳理二、几种特殊四边形的常用判定方法:1.定义:两组对边分别平行;2.两组对边分别相等;3.两组对角分别相等; 4.对角线互相平分; 5.一组对边平行且相等. 1.定义:有一个角是直角的平行四边形; 2.对角线相等的平行四边形; 3.有三个角是直角的四边形.1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形; 3.四条边都相等的四边形.1.定义:一组邻边相等且有一个角是直角的平行四边形;2.有一组邻边相等的矩形; 3.有一个角是直角的菱形.知识梳理三、平行四边形、矩形、菱形、正方形之间的关系 矩形 菱形正方形平行四边形知识梳理三、平行四边形、矩形、菱形、正方形之间的关系有一组邻边相等有一个角是直角有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等知识梳理四、其他重要概念及性质1.两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线间的距离.两条平行线间的距离处处相等.知识梳理四、其他重要概念及性质2.三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. 知识梳理四、其他重要概念及性质3.直角三角形斜边上的中线:直角三角形斜边上的中线等于斜边的一半. 知识梳理考点梳理01平行四边形的性质与判定例1.如图,点B,E分别在AC,DF上,AF分别交BD,CE于点M,N,∠A=∠F,∠1=∠2.(1)求证:四边形BCED是平行四边形;证明:∵∠A=∠F,∴DE∥BC.∵∠1=∠2,且∠1=∠DMF,∴∠DMF=∠2.∴DB∥EC.∴四边形BCED为平行四边形.考点解析(2)已知DE=2,连接BN.若BN平分∠DBC,求CN的长.解:∵BN平分∠DBC,∴∠DBN=∠CBN.∵EC∥DB,∴∠CNB=∠DBN.∴∠CNB=∠CBN.∴CN=BC.由(1)可知四边形BCED是平行四边形.∴BC=DE=2.∴CN=2.考点解析 C考点解析 CB迁移应用【1-3】如图,在□ABCD中,BN=DM,BE=DF,求证:四边形MENF是平行四边形.证明:∵四边形ABCD是平行四边形∴BC//AD∴∠EBN= ∠FDM∵BN=DM,BE=DF∴△EBN≌△FDM (SAS)∴EN=FM,∠BEN= ∠DFM∴∠FEN=∠EFM∴EN// FM∴四边形MENF是平行四边形迁移应用【1-4】如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.(1)求证:四边形AECD是平行四边形;证明:∵∠ACB=∠CAD=90°,∴AD∥CE.∵AE∥DC,∴四边形AECD是平行四边形.迁移应用(2)若AE平分∠BAC,BE=5,BF=4,求AD的长. 迁移应用02三角形的中位线的应用例3.如图,在△ABC中,点M,N分别是AB,AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,求CD的长. 考点解析证明:取AC的中点F,连接BF.∵BD=AB,∴BF为△ADC的中位线,∴DC=2BF.∵E为AB的中点,AB=AC,∴BE=CF,∠ABC=∠ACB.∵BC=CB,∴△EBC≌△FCB,∴CE=BF,∴CD=2CE.F例4.如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.考点解析例5.如图,在Rt△ABC中,∠BAC=90°,点E,F分别是BC,AC的中点,延长BA到点D,使得AB=2AD,连接DE,DF,AE,EF,AF与DE相交于点O.(1)求证:AF与DE互相平分;证明:∵点E,F分别是BC,AC的中点,∴EF∥AB,AB=2EF.∵AB=2AD,点D是BA延长线上的一点,∴AD=EF,AD∥EF.∴四边形ADFE是平行四边形.∴AF与DE互相平分.考点解析(2)如果AB=6,BC=10,求DO的长. 考点解析【2-1】如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数. 迁移应用【2-2】如图,E、F、G、H分别为四边形ABCD四边之中点.求证:四边形EFGH为平行四边形. 迁移应用【2-3】如图,在△ABC中,M是BC的中点,AN⊥BN于N点,AN平分∠BAC, 且AB=12, AC=16, 求MN的长. 迁移应用03矩形的性质与判定例6.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数. 考点解析例7.如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.证明:连接DE.∵AD =AE,∴∠AED =∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC, ∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.又∵DE=DE,∴△DFE≌△DCE,∴DF=DC.考点解析例8.在矩形ABCD中,AB=4,BC=3.若点P是CD上任意一点,如图①,PE⊥BD于点E,PF⊥AC于点F.(1)猜想PE和PF之间有怎样的数量关系?写出你的理由.(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系 (3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程.考点解析(1)猜想PE和PF之间有怎样的数量关系?写出你的理由. 考点解析(2)当点P是AD上任意一点时,如图②,猜想PE和PF之间的数量关系; 考点解析(3)当点P是DC上任意一点时,如图③,猜想PE和PF之间有怎样的数量关系?写出推理过程. 考点解析 迁移应用【3-2】如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.(1)若AB=4,BC=3,求AE的长. 迁移应用【3-2】如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.(2)连接DF,若点D,F,E在同一条直线上,且DF=2,求AE的长. 迁移应用 迁移应用 迁移应用 迁移应用 04直角三角形斜边中线性质考点解析【4-1】如图,在Rt△ABC中,∠ACB=90°, 点D、E、F分别是边AB、BC、CA的中点.若CD+EF=8,则CD的长为______.4迁移应用【4-2】如图,在□ABCD中,E、F、G分别为AD、OB、OC的中点,且2AB=AC, 求证: EF=GF.证明:连接AF.∵四边形ABCD是平行四边形.∴AD=BC,AC=2AO∵2AB=AC, ∴AB=AO∵F是OB的中点,∴AF⊥OB迁移应用【4-2】如图,在□ABCD中,E、F、G分别为AD、OB、OC的中点,且2AB=AC, 求证: EF=GF. 迁移应用05菱形的性质与判定例10.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.证明:∵四边形ABCD为菱形,∴AD∥BC,AD=BA, ∠ABC=∠ADC=2∠ADB ,∴∠DAE=∠AEB,∵AB=AE,∴∠ABC=∠AEB, ∴∠ABC=∠DAE, ∵∠DAE=2∠BAE,∴∠BAE=∠ADB. 又∵AD=BA ,∴△AOD≌△BEA ,∴AO=BE .考点解析 考点解析(1)求证:四边形EBFD为菱形; 考点解析 考点解析【5-1】如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判定□ ADCE是菱形的是( )A.∠BAC=90° B.∠DAE=90° C. AB=AC D. AB=AEA迁移应用 A迁移应用【5-3】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.证明:∵四边形ABCD是菱形∴AC⊥BD,AB // CD,OB=OD∴∠DCO+∠CDO=90°,∠CDO=∠HBO∵DH⊥AB∴OH是Rt△BDH斜边BD上的中线∴OH=OB∴∠OHB=∠HBO ∴∠OHB=∠CDO∵∠DHO+∠OHB=90° ∴∠DHO=∠DCO迁移应用【5-4】如图,四边形ABCD是菱形,∠BAD=60°, 点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,点F在AD的延长线上,CF⊥AD.(1)求证:四边形CEHF是菱形; 迁移应用(2)若四边形CEHF的面积为18,求菱形ABCD的面积. 迁移应用06正方形的性质与判定例12.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.解:连接PC,AC.∵四边形ABCD是正方形,∴∠FCE=90°, AC垂直平分BD,∴AP=PC.又∵PE⊥BC ,PF⊥DC,∴四边形PECF是矩形,∴PC=EF.∴AP=EF.考点解析例13.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.(1)求证:BF=DE;(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.(1)证明:∵正方形ABCD,∴AB=AD,∠BAD=90°,∵AF⊥AC,∴∠EAF=90°,∴∠BAF=∠EAD,在△ADE和△ABF中,AD=AB ,∠DAE=∠BAF ,AE=AF ,∴△ADE≌△ABF(SAS),∴BF=DE;考点解析 考点解析【6-1】如图,正方形ABCD的两条对角线AC,BD交于点O,点E在BD上,且BE=CD, 则∠BEC的度数为_________.【6-2】如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.67.5° 迁移应用【6-3】如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连接AF、BD,延长BD交AF于H.求证: BH⊥AF.证明:∵四边形AEDC和BCFG是正方形∴AC=DC,CF=CB, ∠ACF=∠BCF=90°∴△ACF≌△DCB (SAS)∴∠AFC=∠DBC又∵∠AFC+∠CAF=90°∴∠DBC+ ∠CAF=90°∴∠AHB=90° 即 BH⊥AF迁移应用【6-4】如图,在正方形ABCD中,Q在CD上,且DQ=CQ,P在BC上,AP=CD+CP,求证: AQ平分∠DAP.证明:延长AQ交BC延长线与E.∵四边形ABCD是正方形∴AD=CD,AD// BC∵∠D=∠QCE,∠DAQ=∠E又∵DQ=CQ∴△ADQ≌△ECQ (AAS)∴AD=CE迁移应用【6-4】如图,在正方形ABCD中,Q在CD上,且DQ=CQ,P在BC上,AP=CD+CP,求证: AQ平分∠DAP.∴CD=CE∴AP=CD+CP=CE+CP=EP∴∠PAQ=∠E∴∠PAQ=∠DAQ,即AQ平分∠DAP迁移应用07中点四边形问题例14.如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE.连接AC,BD.(1)试说明四边形EFGH为平行四边形; 考点解析(2)当AC与BD满足_________时,四边形EFGH是菱形,并证明你的结论; AC=BD考点解析(3)当AC与BD满足__________时,四边形EFGH是矩形;当AC与BD满足__________________ 时,四边形EFGH是正方形(不用证明).AC⊥BD AC⊥BD且AC=BD 考点解析08特殊平行四边形中的定值、最值问题例15.如图,正方形ABCD的边长为4,点E在边AB上,AE=1.若点P为对角线BD上的一个动点,则△PAE周长的最小值是( )A.3 B.4 C.5 D.6D考点解析 提示:分别过点P、点M作BC边的垂线. 考点解析课程结束
相关资料
更多









