数学八年级下册第十八章 平行四边形综合与测试精品复习课件ppt

这是一份数学八年级下册第十八章 平行四边形综合与测试精品复习课件ppt，文件包含1832《章末复习特殊平行四边形性质综合运用及动点问题》课件29张pptx、1832《动点问题》同步练习docx、1832《特殊的平行四边形性质》同步练习docx、1832《章末复习特殊平行四边形性质综合运用及动点问题》教学设计教案docx等4份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

章末复习（专题小结）有理数
特殊平行四边形性质综合运用及动点问题
特殊平行四边形性质综合运用
1．【中考·沈阳】如图，在菱形ABCD中，对角线AC与BD交于点O，过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E. (1)求证：四边形OCED是矩形；
证明：∵四边形ABCD为菱形，∴AC⊥BD.∴∠COD＝90°.∵CE∥OD，DE∥OC，∴四边形OCED是平行四边形．又∵∠COD＝90°，∴四边形OCED是矩形．
(2)若CE＝1，DE＝2，则菱形ABCD的面积是________．
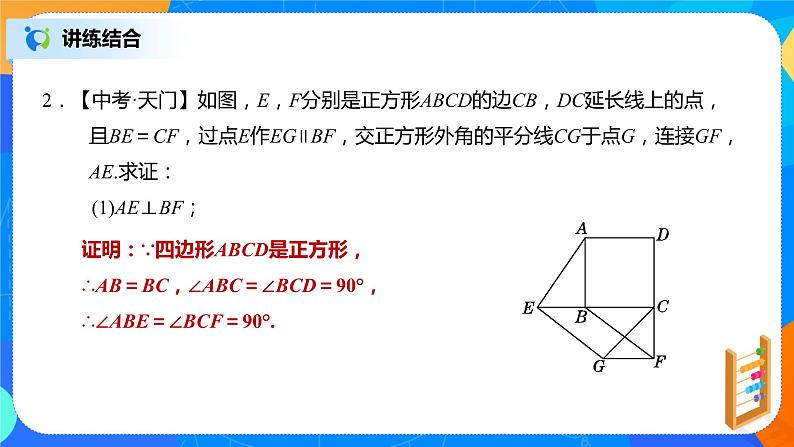
2．【中考·天门】如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE＝CF，过点E作EG∥BF，交正方形外角的平分线CG于点G，连接GF，AE.求证： (1)AE⊥BF；
证明：∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠BCD＝90°，∴∠ABE＝∠BCF＝90°.
(2)四边形BEGF是平行四边形．
证明：延长AB至点P，使BP＝BE，连接EP，如图所示．则AP＝CE，∠EBP＝90°，∴∠P＝45°.∵CG为正方形ABCD外角的平分线，∴∠ECG＝45°，∴∠P＝∠ECG.由(1)得∠BAE＝∠CEG.在△APE和△ECG中，
解：四边形MEBF是正方形．证明：∵四边形ABCD是矩形，∴∠ABC＝90°.∵ME⊥AB，MF⊥BC，∴∠MEB＝∠MFB＝90°.∴四边形MEBF是矩形．又∵BM是∠ABC的平分线，∴ME＝MF.∴四边形MEBF是正方形．
3．如图，在矩形ABCD中，∠ABC的平分线交对角线AC于点M，ME⊥AB，MF⊥BC，垂足分别是E，F.判定四边形MEBF的形状，并证明你的结论．
4．【中考·海南】如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点(与点A，D不重合)，射线PE与BC的延长线交于点Q.(1)求证△PDE≌△QCE.
证明：∵四边形ABCD是正方形，∴∠D＝∠BCD＝90°，∴∠ECQ＝90°＝∠D.∵E是CD的中点，∴DE＝CE.又∵∠DEP＝∠CEQ，∴△PDE≌△QCE.
(2)过点E作EF∥BC交PB于点F，连接AF，当PB＝PQ时，①求证：四边形AFEP是平行四边形；
∴∠3＝∠4.又∵AD∥BC，EF∥BC，∴AD∥EF，∴∠1＝∠4，∴∠2＝∠3.又∵PF＝FP，∴△APF≌△EFP，∴AP＝EF.又∵AP∥EF，∴四边形AFEP是平行四边形．
②请判断四边形AFEP是否为菱形，并说明理由．
特殊四边形的性质在动点问题中的巧用
1．如图，在▱ABCD中，E，F两点在对角线BD上运动(E，F不重合)，且保持BE＝DF，连接AE，CF.请你猜想AE与CF有怎样的数量关系和位置关系，并说明理由．
解：AE＝CF，AE∥CF.理由如下：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.∴∠ABE＝∠CDF.又∵BE＝DF，∴△ABE≌△CDF(SAS)．∴AE＝CF，∠AEB＝∠CFD.∵∠AEB＋∠AED＝∠CFD＋∠CFB＝180°，∴∠AED＝∠CFB.∴AE∥CF.
2．在菱形ABCD中，∠B＝60°，动点E在边BC上，动点F在边CD上．(1)如图①，若E是BC的中点，∠AEF＝60°，求证BE＝DF；
证明：连接AC.∵在菱形ABCD中，∠B＝60°，AB＝BC＝CD，AB∥CD，∴∠BCD＝180°－∠B＝120°，△ABC是等边三角形．又∵E是BC的中点，∴AE⊥BC.∵∠AEF＝60°，∴∠FEC＝90°－∠AEF＝30°.∴∠CFE＝180°－∠FEC－∠BCD＝180°－30°－120°＝30°. ∴∠FEC＝∠CFE.∴EC＝CF. ∴BE＝DF.
证明：连接AC.由(1)知△ABC是等边三角形，∴AB＝AC，∠ACB＝∠BAC＝∠EAF＝60°.∴∠BAE＝∠CAF.∵∠BCD＝120°，∠ACB＝60°，∴∠ACF＝60°＝∠B.∴△ABE≌△ACF. ∴AE＝AF.又∵∠EAF＝60°，∴△AEF是等边三角形．
(2)如图②，若∠EAF＝60°，求证：△AEF是等边三角形．
解：∵四边形ABCD是矩形，∴AD∥BC，∠B＝90°.∴∠OAE＝∠OCF，∠AEO＝∠CFO.∵EF垂直平分AC，垂足为O，∴OA＝OC.∴△AOE≌△COF(AAS)． ∴OE＝OF.
3．在矩形ABCD中，AB＝4 cm，BC＝8 cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为O.(1)如图①，连接AF，CE，证明四边形AFCE为菱形，并求AF的长．
∴四边形AFCE为平行四边形．又∵EF⊥AC，∴四边形AFCE为菱形．∴AF＝CF.设AF＝CF＝x cm，则BF＝(8－x)cm.在Rt△ABF中，AB＝4 cm，由勾股定理得42＋(8－x)2＝x2，解得x＝5.∴AF＝5 cm.
(2)如图②，动点P，Q分别从A，C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，已知点P的速度为5 cm/s，点Q的速度为4 cm/s，运动时间为t s，当以A，C，P，Q四点为顶点的四边形是平行四边形时，求t的值．
解：显然当P点在AF上，Q点在CD上时，以A，C，P，Q四点为顶点不可能构成平行四边形；同理，当P点在AB上，Q点在DE或CE上时，也不可能构成平行四边形．因此只有当P点在BF上，Q点在ED上时，才能构成平行四边形．如图，连接AP，CQ.若以A，C，P，Q四点为顶点的四边形是平行四边形，则PC＝QA.
4．【教材P62习题T13拓展】如图，正方形ABCD的边长为8 cm，E，F，G，H分别是AB，BC，CD，DA上的动点，且AE＝BF＝CG＝DH.(1)求证：四边形EFGH是正方形；
证明：如图所示．∵四边形ABCD为正方形，∴∠A＝∠ABC＝∠C＝∠ADC＝90°，AB＝BC＝CD＝AD.又∵AE＝BF＝CG＝DH，∴BE＝CF＝DG＝AH.
∴△AEH≌△BFE≌△CGF≌△DHG.∴EH＝EF＝FG＝GH，∠1＝∠2.∴四边形EFGH为菱形．∵∠1＋∠3＝90°，∠1＝∠2，∴∠2＋∠3＝90°.∴∠HEF＝90°.又∵四边形EFGH为菱形，∴四边形EFGH是正方形．
(2)判断直线EG是否经过一个定点，并说明理由．
【点拨】解动点问题的关键是把动点看成定点，找到等量关系，一般情况下，这个等量关系在点运动时仍然成立．