资料中包含下列文件,点击文件名可预览资料内容







当前文件暂不支持在线预览,请下载使用
还剩17页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学九年级下册 3.1 《圆》课件+分层练习(含答案解析)
展开
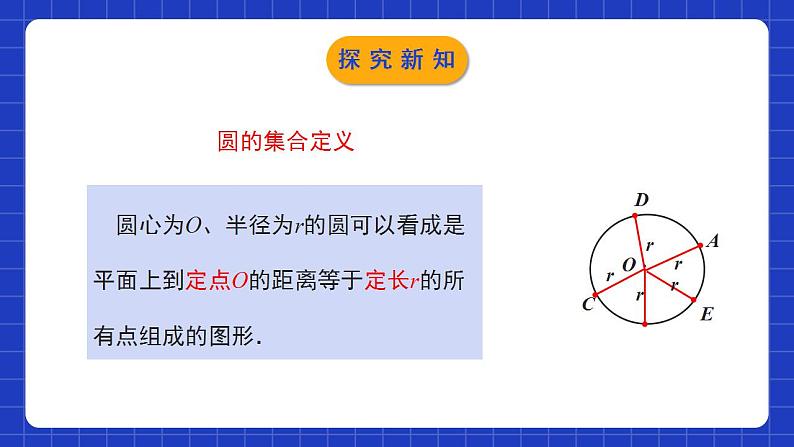
3.1圆学习目标理解如何确定点与圆的位置关系。理解并掌握圆的有关概念。能灵活运用圆的有关概念解决相关的实际问题。一切平面图形中最美的是圆——毕达哥拉斯圆象征着圆满和谐情境导入圆是常见的图形,生活中的许多物体都给我们以圆的形象 情境导入探究圆的概念我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?探究新知圆的旋转定义(动态定义) 在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”. 固定的端点O叫做圆心,线段OA叫做半径,一般用r表示.AOr探究新知圆的集合定义 圆心为O、半径为r的圆可以看成是平面上到定点O的距离等于定长r的所有点组成的图形.O·ACErrrrrD探究新知归纳总结(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);(圆的性质)(2)到定点的距离等于定长的点都在同一个圆上.(圆的判定)(3)确定一个圆的两个要素:圆心、半径. 圆心确定圆的位置,半径确定圆的大小.探究新知 一些学生正在做投圈游戏,他们的投圈目标都是图中的花瓶,他们呈“一”字排开.问题:这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形?每个人到花瓶的距离相等时才公平.探究新知他们应当站在以花瓶为圆心的同一个圆上才公平 花瓶探究新知圆的有关概念AB圆上任意两点间的部分叫做圆弧,简称弧.M探究新知B连接圆上任意两点间的线段叫做弦.(如弦AB)经过圆心的弦叫做直径.(如直径CD)DCA圆的任意一条直径将圆分成两条弧,每一条弧都叫半圆.探究新知BDCA能够重合的两个圆叫做等圆.在同圆或等圆中,能够互相重合的弧叫做等弧.半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等.注意:等弧不是指弧长相等.探究新知点和圆的位置关系投镖游戏
如图:是一个圆形耙的示意图,O为圆心,小明向上投了5枝飞镖,它们分别落到了A、B、C、D、E点。观察A、B、C、D、E这5个点与⊙O的位置关系 ?探究新知点与圆的位置关系有三种:点在圆外、点在圆上、点在圆内.探究新知d₁d₃d₂归纳总结探究新知1. 下列关于圆的叙述中正确的是( )A.圆是由圆心唯一确定的B.圆是一条封闭的曲线C.平面上到定点的距离小于或等于定长的所有点组成圆D.圆内任意一点到圆心的距离都相等B随堂练习2. ⊙O的半径为5 cm,点A到圆心O的距离OA=3 cm,则点A与⊙O的位置关系为( )A.点A在圆上 B.点A在圆内C.点A在圆外 D.无法确定B随堂练习3.下列关于圆的叙述中正确的是( )A.圆是由圆心唯一确定的B.圆是一条封闭的曲线C.平面上到定点的距离小于或等于定长的所有点组 成圆D.圆内任意一点到圆心的距离都相等B随堂练习4.平面内已知点P,以P为圆心,3 cm为半径作圆,这样的圆可以作( )A.1个 B.2个 C.3个 D.无数个A随堂练习5.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 . 圆内圆上圆外6.已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 . OA>3305 cm=r,∴点Q 在⊙ O 外.∵ RD=3 cm,OD=3 cm,且OD ⊥ l,∴ OR= = cm<5 cm=r.∴点R 在⊙ O 内.随堂练习1.理解圆的定义要注意两层含义: (1)静态定义 (2)动态定义.2.与圆有关的概念 弦与直径,弧、半圆、优弧、劣弧,等圆与等弧,3.点和圆的位置关系: 点在圆外、点在圆上、点 在圆内.课堂小结课程结束
相关资料
更多









