

还剩33页未读,
继续阅读
成套系列资料,整套一键下载
苏科版数学七年级上册同步专题热点难点练习 专题2.5 有理数(章节复习+能力强化卷)学生版+教师版
展开
这是一份苏科版数学七年级上册同步专题热点难点练习 专题2.5 有理数(章节复习+能力强化卷)学生版+教师版,共36页。
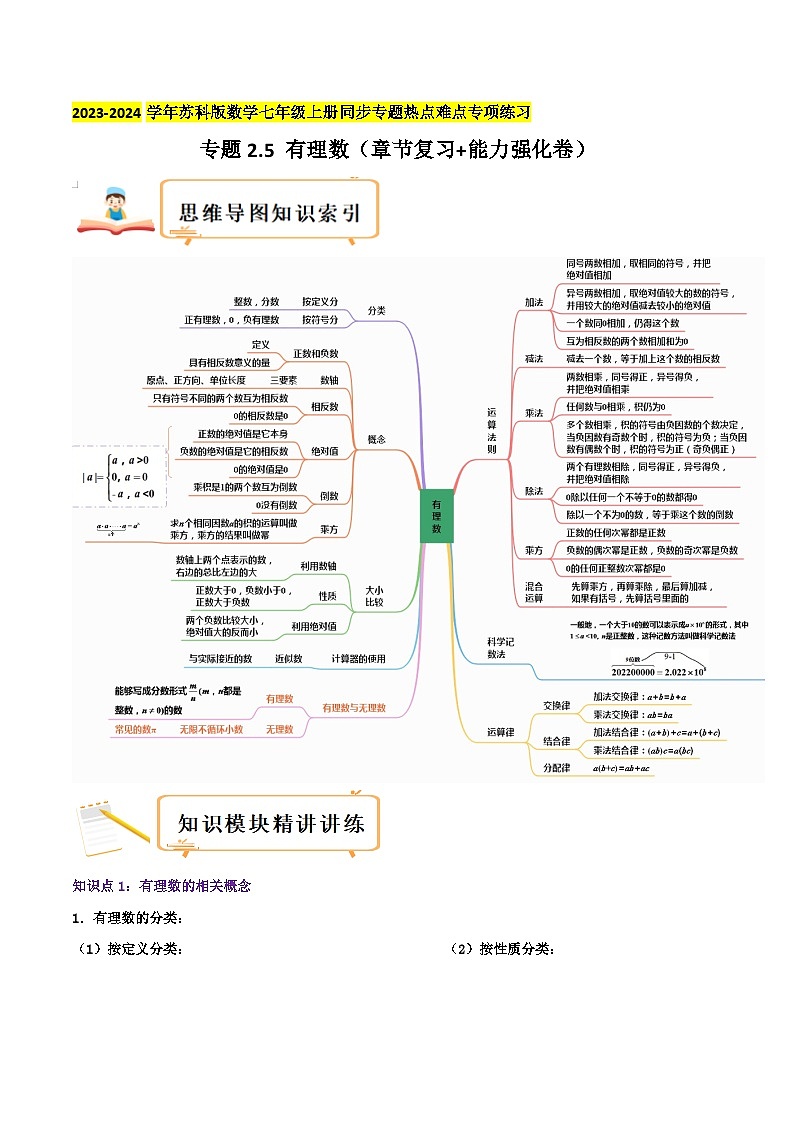
2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题2.5 有理数(章节复习+能力强化卷)知识点1:有理数的相关概念 1.有理数的分类: (1)按定义分类: (2)按性质分类:细节剖析(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:2.数轴:规定了原点、正方向和单位长度的直线.细节剖析(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0. 细节剖析(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“ 号即可.(3)多重符号的化简:数字前面“”号的个数若有 个时,化简结果为正,若有奇数个时,化简结果为 细节剖析(1)代数意义:一个正数的 是它本身;一个负数的绝对值是它的 ;0的绝对值是 . 数a的绝对值记作 .(2)几何意义:一个数a的 就是数轴上表示数a的点与原点的 .知识点2:有理数的运算 1 .法则:(1)加法法则:①同号两数 ,取 的符号,并把 相加.②绝对值不相等的异号两数 ,取绝对值 的加数的符号,并用 的绝对值减去 的绝对值.③一个数同 相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的 .即a-b= .(3)乘法法则:①两数相乘,同号得 ,异号得 ,并把 相乘.②任何数同 相乘,都得 (4)除法法则:除以一个不等于0的数,等于乘这个数的 .即a÷b=a·(b≠0) . (5)乘方运算的符号法则:①负数的奇次幂是 ,负数的偶次幂是 ;②正数的任何次幂都是 ,0的任何非零次幂都是 . (6)有理数的混合运算顺序:①先 ,再 ,最后 ;②同级运算,从 进行;③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.细节剖析 “奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是 的个数,正负指结果中积的 ,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是 ,当底数为 时,指数为奇数,则幂为负;指数为 ,则幂为正,例如: , .细节剖析(1)交换律: ① 加法交换律:a+b= ; ②乘法交换律:ab=ba;(2)结合律: ①加法结合律: (a+b)+c= ; ②乘法结合律:(ab)c= (3)分配律:a(b+c)= 知识点3:有理数的大小比较比较大小常用的方法有:(1) 比较法;(2) 比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 比较法.(4) 比较法;(5) 比较法.知识点4:科学记数法、近似数及精确度 1.科学记数法:把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做 .例如:200 000=.2.近似数:接近准确数而不等于准确数的数,叫做这个精确数的 或 .如长江的长约为6300㎞,这里的6300㎞就是 .细节剖析一般采用四舍五入法取 ,只要看要保留位数的下一位是 3.精确度:一个近似数四舍五入到哪一位,就称这个数精确到哪一位,精确到的这一位也叫做这个近似数的精确度. 细节剖析(1)精确度是指 与 的接近程度.(2)精确度有两种形式:①精确到哪一位.②保留几个 .这两种的形式的意义不一样,一般来说精确到哪一位可以表示误差绝对值的大小,例如精确到米,说明结果与实际数相差不超过米,而有效数字往往用来比较几个近似数哪个更精确些.一、选择题(共10题;每题2分,共20分)1.(2分)(2023七上·海曙期末)宁波文创港三期已正式开工建设,总建筑面积约,272000用科学记数法表示,正确的是( )A. B. C. D.2.(2分)(2023七上·兰溪期末)计算的结果是( )A.-1 B. C. D.3.(2分)(2023七上·江北期末)实数,在数轴上的位置如图所示,下列说法一定正确的是( )A. B. C. D.4.(2分)(2023七上·宁海期末)已知有理数a,b在数轴上如图所示,则下列式子错误的是( )A. B. C. D.5.(2分)(2023七上·通川期末)如图,数轴上点M,P,N分别表示数m,m+n,n,那么原点的位置是( )A.在线段MP上 B.在线段PN上 C.在点M的左侧 D.在点N的右侧6.(2分)(2022七上·乐山期中)一电子跳蚤落在数轴上的某点k0处,第一步从k0向左跳一个单位到k1,第二步从k1向右跳2个单位到k2,第三步由k2处向左跳3个单位到k3,第四步由k3向右跳4个单位k4,….按以上规律跳了100步后,电子跳蚤落在数轴上的数是0,则k0表示的数是A.0 B.100 C.50 D.7.(2分)(2022七上·金东期中)任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如,仿此,若m3的“分裂数”中有一个是59,则m的值为( )A.6 B.7 C.8 D.98.(2分)在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段 的长度为( ) A.4.5 B.1.5 C.6.5或1.5 D.4.5或1.59.(2分)(2021七上·安吉期末)如图,已知正方形的边长为24厘米,甲,乙两动点分别从正方形ABCD的顶点D,B同时沿正方形的边开始移动,甲点按顺时针方向环行,乙点按逆时针方向环行,若乙的速度为9厘米/秒,甲的速度为3厘米/秒,当它们运动了2022秒时,它们在正方形边上相遇了( )A.252 次 B.253次 C.254次 D.255次10.(2分)(2021七上·长沙期末)如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒).若点P在运动过程中,当PB=2时,则运动时间t的值为( ) A. 秒或 秒B. 秒或 秒或 秒或 秒C.3秒或7秒或 秒或 秒D. 秒或 秒或 秒或 秒二、填空题(共10题;每题2分,共20分)11.(2分)(2023七上·东方期末)某地一天早晨的气温是,中午温度上升了,则中午的气温是 ℃.12.(2分)有理数,,在数轴上对应的点的位置如图所示,下列各式正确的是 (填序号即可). ①;②;③;④13.(2分)(2023七上·西安期末)如果有理数a、b、c在数轴上的位置如图所示,则 .14.(2分)(2023七上·通川期末)若,则 .15.(2分)(2023七上·宣汉期末)若与互为相反数,则的值是 .16.(2分)(2022七上·大冶期末)m是常数,若式子的最小值是6,则m的值是 .17.(2分)—动点P从数轴上的原点出发,按下列规则运动:①沿数轴的正方向先前进5个单位,然后后退3个单位,如此反复进行.②已知点P每秒只能前进或后退1个单位,设表示第n秒点P在数轴上的位置所对应的数,则为 .18.(2分)(2022七上·宁波期中)设三个互不相等的有理数,既可表示为1、a+b、a的形式,又可表示为4、、b的形式,则(b﹣a)3的值为 .19.(2分)(2022七上·义乌月考)已知点O是数轴的原点,点A、B、C在数轴上对应的数分别是﹣12、b、c,且b、c满足(b﹣9)2+|c﹣15|=0,动点P从点A出发以2单位/秒的速度向右运动,同时点Q从点C出发,以1个单位/秒速度向左运动,O、B两点之间为“变速区”,规则为从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速,从点B运动到点O期间速度变为原来的3倍,之后立刻恢复原速,运动时间为 秒时,P、Q两点到点B的距离相等.20.(2分)(2022七上·杭州月考)在数轴上和有理数a,b,c对应的点的位置如图所示,有下面四个结论:①,②,③,④,⑤其中,正确的结论有 (填序号).三、解答题(共9题;共60分)21.(6分)(2023七上·西安期末)计算(1)(3分); (2)(3分).22.(5分)(2023七上·陈仓期末)数学老师规定了一种新运算:若,是有理数,则,请你计算:;.23.(5分)(2023七上·洛川期末)如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,设点A,B,C所对应数的和是m.若以B为原点,求出点A,C所对应的数,并计算m的值;若以C为原点,m又是多少?24.(8分)(2023七上·杭州期末)在实数范围内定义运算“※”:,例如:.(1)(2分)若,,计算的值.(2)(3分)若,求x的值.(3)(3分)若,求的值.25.(6分)(2023七上·韩城期末)如图,数轴上从左到右依次有点、、、,其中点为原点,、所对应的数分别为、1,、两点间的距离是3.(1)(3分)在图中标出点,的位置,并写出点对应的数;(2)(3分)若在数轴上另取一点,且、两点间的距离是7,求点所对应的数.26.(8分)(2023七上·兰溪期末)小明爸爸在一家电信公司了解到两种移动电话计费方法:计费方法A是每月收月租费30元,通话时间120分钟内免费,超过120分的部分按每分钟0.25元加收通话费;计费方法B是每月收月租费50元,通话时间200分钟内免费,超过200分的部分按每分钟0.2元收通话费.(1)(2分)若小明爸爸一个月的通话时间大约在150分钟和160分钟之间,请通过计算说明选用哪种计费方式,可以节省费用?(2)(3分)小明爸爸当前选择了计费方式A,有一个月累计通话240分钟,话费m元.若改成用计费方法B,则同样话费m元,可多通话多少分钟?(3)(3分)从节省话费的角度考虑,帮小明爸爸选择合适的计费方式.27.(7分)(2023七上·慈溪期末)2022年天猫平台“双十一”促销活动如火如荼地进行.小明发现天猫平台甲、乙、丙三家店铺在销售同一款标价均为30元的杯子,但三家的促销方式不同,具体优惠信息如下:(1)(2分)若小明想买25个该款杯子,请你帮小明分别计算一下甲、乙、丙三家店铺优惠后的实际价格,再挑选哪家店铺购买更优惠.(2)(2分)若小明想从丙店铺购买n个该款杯子,请用含n的代数式表示优惠后购买的总价.(3)(3分)若小明想花费3000元在丙店铺来购买该款杯子,且恰好用完,则他能买多少个该款杯子?(注:假设小明均一次性购买)28.(7分)(2022七上·延庆期末)已知数轴上两点,,其中表示的数为,表示的数为2.给出如下定义:若在数轴上存在一点,使得,则称点叫做点,的“和距离点”.如图,若点表示的数为0,有,则称点为点,的“5和距离点”.(1)(2分)如果点为点,的“和距离点”,且点在数轴上表示的数为,那么的值是 ;(2)(2分)如果点是数轴上点,的“6和距离点”,那么点表示的数为 ;(3)(3分)如果点在数轴上(不与,重合),满足,且此时点为点,的“和距离点”,求的值.29.(8分)(2023七上·通川期末)阅读下面的材料:我们知道,在数轴上,表示有理数对应的点到原点的距离,同样的道理,表示有理数对应的点到有理数2对应的点的距离,例如,,表示数轴上有理数5对应的点到有理数2对应的点的距离是3. 请根据上面的材料解答下列问题:(1)(2分)请用上面的方法计算数轴上有理数-9对应的点到有理数3对应的点的距离;(2)(2分)填空:表示与理数对应的点与有理数 对应的点的距离;如果,那么有理数的值是 ;(3)(2分)填空:如果,那么有理数的值是 .(4)(2分)是否存在有理数,使等式的结果等于4?如果存在,请直接写出的值;如果不存在,请说明原因. 2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题2.5 有理数(章节复习+能力强化卷)知识点1:有理数的相关概念 1.有理数的分类: (1)按定义分类: (2)按性质分类:细节剖析(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:2.数轴:规定了原点、正方向和单位长度的直线.细节剖析(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0. 细节剖析(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.4.绝对值:(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0. 数a的绝对值记作.(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.知识点2:有理数的运算 1 .法则:(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b) .(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0) . (5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0. (6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行;③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.细节剖析 “奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如: , .2.运算律: (1)交换律: ① 加法交换律:a+b=b+a; ②乘法交换律:ab=ba;(2)结合律: ①加法结合律: (a+b)+c=a+(b+c); ②乘法结合律:(ab)c=a(bc) (3)分配律:a(b+c)=ab+ac知识点3:有理数的大小比较比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 作差比较法.(4)作商比较法;(5)倒数比较法.知识点4:科学记数法、近似数及精确度 1.科学记数法:把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做科学记数法.例如:200 000=.2.近似数:接近准确数而不等于准确数的数,叫做这个精确数的近似数或近似值.如长江的长约为6300㎞,这里的6300㎞就是近似数.细节剖析一般采用四舍五入法取近似数,只要看要保留位数的下一位是舍还是入.3.精确度:一个近似数四舍五入到哪一位,就称这个数精确到哪一位,精确到的这一位也叫做这个近似数的精确度. 细节剖析(1)精确度是指近似数与准确数的接近程度.(2)精确度有两种形式:①精确到哪一位.②保留几个有效数字.这两种的形式的意义不一样,一般来说精确到哪一位可以表示误差绝对值的大小,例如精确到米,说明结果与实际数相差不超过米,而有效数字往往用来比较几个近似数哪个更精确些.一、选择题(共10题;每题2分,共20分)1.(2分)(2023七上·海曙期末)宁波文创港三期已正式开工建设,总建筑面积约,272000用科学记数法表示,正确的是( )A. B. C. D.【答案】B【规范解答】解:.故答案为:B.【思路点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.2.(2分)(2023七上·兰溪期末)计算的结果是( )A.-1 B. C. D.【答案】A【规范解答】解:故答案为:A.【思路点拨】首先利用有理数的减法法则计算出括号中式子的结果,然后利用有理数的除法法则进行计算.3.(2分)(2023七上·江北期末)实数,在数轴上的位置如图所示,下列说法一定正确的是( )A. B. C. D.【答案】D【规范解答】解:由数轴可得:,, A、,故此选项错误;B、,故此选项错误;C、,故此选项错误;D、,故此选项正确.故答案为:D. 【思路点拨】根据数轴提供的信息可得a<0<b,且,据此直接可判断B选项;根据有理数的加法法则,绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,据此可判断A选项;根据有理数的减法法则,较小的数减去较大的数,差一定为负数,据此判断C选项;根据有理数的乘法法则,异号两数相乘,积为负,据此判断D选项.4.(2分)(2023七上·宁海期末)已知有理数a,b在数轴上如图所示,则下列式子错误的是( )A. B. C. D.【答案】D【规范解答】解:根据数轴上的点所表示的数的特点得a<0<b,, ∴a+b<0,,故A、B、C选项都正确,不符合题意; 由于-a是a的相反数,数轴上表示互为相反数的两点位于原点的两侧,并且到原点的距离相等,故表示-a的点在表示b的点的右边,而数轴上的点所表示的数,右边的总是大于左边的,故-a>b,所以D选项,错误,符合题意. 故答案为:D. 【思路点拨】根据数轴上的点所表示的数的特点得a<0<b,,据此可直接判断C选项;进而根据绝对值不相等的异号两数相加,取绝对值较大的加数的符号,可判断A选项;根据异号两数相除,商为负可判断B选项;根据互为相反数的两个数在数轴上的表示方法及数轴上点所表示的数,右边的总是大于左边的可判断D选项.5.(2分)(2023七上·通川期末)如图,数轴上点M,P,N分别表示数m,m+n,n,那么原点的位置是( )A.在线段MP上 B.在线段PN上 C.在点M的左侧 D.在点N的右侧【答案】A【规范解答】解:由点M,P,N的位置可知,m<0<n,且PN<PM,∴n-(m+n)<(m+n)-m,即-m<n,∴|m|<|n|,∴m+n>0,∴原点一定在PM上,且靠近点M.故答案为:A.【思路点拨】根据数轴可得m<0<n,且PN<PM,由两点间距离公式可得PN=n-(m+n),PM=(m+n)-m,由PN
2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题2.5 有理数(章节复习+能力强化卷)知识点1:有理数的相关概念 1.有理数的分类: (1)按定义分类: (2)按性质分类:细节剖析(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:2.数轴:规定了原点、正方向和单位长度的直线.细节剖析(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0. 细节剖析(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“ 号即可.(3)多重符号的化简:数字前面“”号的个数若有 个时,化简结果为正,若有奇数个时,化简结果为 细节剖析(1)代数意义:一个正数的 是它本身;一个负数的绝对值是它的 ;0的绝对值是 . 数a的绝对值记作 .(2)几何意义:一个数a的 就是数轴上表示数a的点与原点的 .知识点2:有理数的运算 1 .法则:(1)加法法则:①同号两数 ,取 的符号,并把 相加.②绝对值不相等的异号两数 ,取绝对值 的加数的符号,并用 的绝对值减去 的绝对值.③一个数同 相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的 .即a-b= .(3)乘法法则:①两数相乘,同号得 ,异号得 ,并把 相乘.②任何数同 相乘,都得 (4)除法法则:除以一个不等于0的数,等于乘这个数的 .即a÷b=a·(b≠0) . (5)乘方运算的符号法则:①负数的奇次幂是 ,负数的偶次幂是 ;②正数的任何次幂都是 ,0的任何非零次幂都是 . (6)有理数的混合运算顺序:①先 ,再 ,最后 ;②同级运算,从 进行;③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.细节剖析 “奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是 的个数,正负指结果中积的 ,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是 ,当底数为 时,指数为奇数,则幂为负;指数为 ,则幂为正,例如: , .细节剖析(1)交换律: ① 加法交换律:a+b= ; ②乘法交换律:ab=ba;(2)结合律: ①加法结合律: (a+b)+c= ; ②乘法结合律:(ab)c= (3)分配律:a(b+c)= 知识点3:有理数的大小比较比较大小常用的方法有:(1) 比较法;(2) 比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 比较法.(4) 比较法;(5) 比较法.知识点4:科学记数法、近似数及精确度 1.科学记数法:把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做 .例如:200 000=.2.近似数:接近准确数而不等于准确数的数,叫做这个精确数的 或 .如长江的长约为6300㎞,这里的6300㎞就是 .细节剖析一般采用四舍五入法取 ,只要看要保留位数的下一位是 3.精确度:一个近似数四舍五入到哪一位,就称这个数精确到哪一位,精确到的这一位也叫做这个近似数的精确度. 细节剖析(1)精确度是指 与 的接近程度.(2)精确度有两种形式:①精确到哪一位.②保留几个 .这两种的形式的意义不一样,一般来说精确到哪一位可以表示误差绝对值的大小,例如精确到米,说明结果与实际数相差不超过米,而有效数字往往用来比较几个近似数哪个更精确些.一、选择题(共10题;每题2分,共20分)1.(2分)(2023七上·海曙期末)宁波文创港三期已正式开工建设,总建筑面积约,272000用科学记数法表示,正确的是( )A. B. C. D.2.(2分)(2023七上·兰溪期末)计算的结果是( )A.-1 B. C. D.3.(2分)(2023七上·江北期末)实数,在数轴上的位置如图所示,下列说法一定正确的是( )A. B. C. D.4.(2分)(2023七上·宁海期末)已知有理数a,b在数轴上如图所示,则下列式子错误的是( )A. B. C. D.5.(2分)(2023七上·通川期末)如图,数轴上点M,P,N分别表示数m,m+n,n,那么原点的位置是( )A.在线段MP上 B.在线段PN上 C.在点M的左侧 D.在点N的右侧6.(2分)(2022七上·乐山期中)一电子跳蚤落在数轴上的某点k0处,第一步从k0向左跳一个单位到k1,第二步从k1向右跳2个单位到k2,第三步由k2处向左跳3个单位到k3,第四步由k3向右跳4个单位k4,….按以上规律跳了100步后,电子跳蚤落在数轴上的数是0,则k0表示的数是A.0 B.100 C.50 D.7.(2分)(2022七上·金东期中)任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如,仿此,若m3的“分裂数”中有一个是59,则m的值为( )A.6 B.7 C.8 D.98.(2分)在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段 的长度为( ) A.4.5 B.1.5 C.6.5或1.5 D.4.5或1.59.(2分)(2021七上·安吉期末)如图,已知正方形的边长为24厘米,甲,乙两动点分别从正方形ABCD的顶点D,B同时沿正方形的边开始移动,甲点按顺时针方向环行,乙点按逆时针方向环行,若乙的速度为9厘米/秒,甲的速度为3厘米/秒,当它们运动了2022秒时,它们在正方形边上相遇了( )A.252 次 B.253次 C.254次 D.255次10.(2分)(2021七上·长沙期末)如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒).若点P在运动过程中,当PB=2时,则运动时间t的值为( ) A. 秒或 秒B. 秒或 秒或 秒或 秒C.3秒或7秒或 秒或 秒D. 秒或 秒或 秒或 秒二、填空题(共10题;每题2分,共20分)11.(2分)(2023七上·东方期末)某地一天早晨的气温是,中午温度上升了,则中午的气温是 ℃.12.(2分)有理数,,在数轴上对应的点的位置如图所示,下列各式正确的是 (填序号即可). ①;②;③;④13.(2分)(2023七上·西安期末)如果有理数a、b、c在数轴上的位置如图所示,则 .14.(2分)(2023七上·通川期末)若,则 .15.(2分)(2023七上·宣汉期末)若与互为相反数,则的值是 .16.(2分)(2022七上·大冶期末)m是常数,若式子的最小值是6,则m的值是 .17.(2分)—动点P从数轴上的原点出发,按下列规则运动:①沿数轴的正方向先前进5个单位,然后后退3个单位,如此反复进行.②已知点P每秒只能前进或后退1个单位,设表示第n秒点P在数轴上的位置所对应的数,则为 .18.(2分)(2022七上·宁波期中)设三个互不相等的有理数,既可表示为1、a+b、a的形式,又可表示为4、、b的形式,则(b﹣a)3的值为 .19.(2分)(2022七上·义乌月考)已知点O是数轴的原点,点A、B、C在数轴上对应的数分别是﹣12、b、c,且b、c满足(b﹣9)2+|c﹣15|=0,动点P从点A出发以2单位/秒的速度向右运动,同时点Q从点C出发,以1个单位/秒速度向左运动,O、B两点之间为“变速区”,规则为从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速,从点B运动到点O期间速度变为原来的3倍,之后立刻恢复原速,运动时间为 秒时,P、Q两点到点B的距离相等.20.(2分)(2022七上·杭州月考)在数轴上和有理数a,b,c对应的点的位置如图所示,有下面四个结论:①,②,③,④,⑤其中,正确的结论有 (填序号).三、解答题(共9题;共60分)21.(6分)(2023七上·西安期末)计算(1)(3分); (2)(3分).22.(5分)(2023七上·陈仓期末)数学老师规定了一种新运算:若,是有理数,则,请你计算:;.23.(5分)(2023七上·洛川期末)如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,设点A,B,C所对应数的和是m.若以B为原点,求出点A,C所对应的数,并计算m的值;若以C为原点,m又是多少?24.(8分)(2023七上·杭州期末)在实数范围内定义运算“※”:,例如:.(1)(2分)若,,计算的值.(2)(3分)若,求x的值.(3)(3分)若,求的值.25.(6分)(2023七上·韩城期末)如图,数轴上从左到右依次有点、、、,其中点为原点,、所对应的数分别为、1,、两点间的距离是3.(1)(3分)在图中标出点,的位置,并写出点对应的数;(2)(3分)若在数轴上另取一点,且、两点间的距离是7,求点所对应的数.26.(8分)(2023七上·兰溪期末)小明爸爸在一家电信公司了解到两种移动电话计费方法:计费方法A是每月收月租费30元,通话时间120分钟内免费,超过120分的部分按每分钟0.25元加收通话费;计费方法B是每月收月租费50元,通话时间200分钟内免费,超过200分的部分按每分钟0.2元收通话费.(1)(2分)若小明爸爸一个月的通话时间大约在150分钟和160分钟之间,请通过计算说明选用哪种计费方式,可以节省费用?(2)(3分)小明爸爸当前选择了计费方式A,有一个月累计通话240分钟,话费m元.若改成用计费方法B,则同样话费m元,可多通话多少分钟?(3)(3分)从节省话费的角度考虑,帮小明爸爸选择合适的计费方式.27.(7分)(2023七上·慈溪期末)2022年天猫平台“双十一”促销活动如火如荼地进行.小明发现天猫平台甲、乙、丙三家店铺在销售同一款标价均为30元的杯子,但三家的促销方式不同,具体优惠信息如下:(1)(2分)若小明想买25个该款杯子,请你帮小明分别计算一下甲、乙、丙三家店铺优惠后的实际价格,再挑选哪家店铺购买更优惠.(2)(2分)若小明想从丙店铺购买n个该款杯子,请用含n的代数式表示优惠后购买的总价.(3)(3分)若小明想花费3000元在丙店铺来购买该款杯子,且恰好用完,则他能买多少个该款杯子?(注:假设小明均一次性购买)28.(7分)(2022七上·延庆期末)已知数轴上两点,,其中表示的数为,表示的数为2.给出如下定义:若在数轴上存在一点,使得,则称点叫做点,的“和距离点”.如图,若点表示的数为0,有,则称点为点,的“5和距离点”.(1)(2分)如果点为点,的“和距离点”,且点在数轴上表示的数为,那么的值是 ;(2)(2分)如果点是数轴上点,的“6和距离点”,那么点表示的数为 ;(3)(3分)如果点在数轴上(不与,重合),满足,且此时点为点,的“和距离点”,求的值.29.(8分)(2023七上·通川期末)阅读下面的材料:我们知道,在数轴上,表示有理数对应的点到原点的距离,同样的道理,表示有理数对应的点到有理数2对应的点的距离,例如,,表示数轴上有理数5对应的点到有理数2对应的点的距离是3. 请根据上面的材料解答下列问题:(1)(2分)请用上面的方法计算数轴上有理数-9对应的点到有理数3对应的点的距离;(2)(2分)填空:表示与理数对应的点与有理数 对应的点的距离;如果,那么有理数的值是 ;(3)(2分)填空:如果,那么有理数的值是 .(4)(2分)是否存在有理数,使等式的结果等于4?如果存在,请直接写出的值;如果不存在,请说明原因. 2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题2.5 有理数(章节复习+能力强化卷)知识点1:有理数的相关概念 1.有理数的分类: (1)按定义分类: (2)按性质分类:细节剖析(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:2.数轴:规定了原点、正方向和单位长度的直线.细节剖析(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0. 细节剖析(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.4.绝对值:(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0. 数a的绝对值记作.(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.知识点2:有理数的运算 1 .法则:(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b) .(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0) . (5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0. (6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行;③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.细节剖析 “奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如: , .2.运算律: (1)交换律: ① 加法交换律:a+b=b+a; ②乘法交换律:ab=ba;(2)结合律: ①加法结合律: (a+b)+c=a+(b+c); ②乘法结合律:(ab)c=a(bc) (3)分配律:a(b+c)=ab+ac知识点3:有理数的大小比较比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 作差比较法.(4)作商比较法;(5)倒数比较法.知识点4:科学记数法、近似数及精确度 1.科学记数法:把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做科学记数法.例如:200 000=.2.近似数:接近准确数而不等于准确数的数,叫做这个精确数的近似数或近似值.如长江的长约为6300㎞,这里的6300㎞就是近似数.细节剖析一般采用四舍五入法取近似数,只要看要保留位数的下一位是舍还是入.3.精确度:一个近似数四舍五入到哪一位,就称这个数精确到哪一位,精确到的这一位也叫做这个近似数的精确度. 细节剖析(1)精确度是指近似数与准确数的接近程度.(2)精确度有两种形式:①精确到哪一位.②保留几个有效数字.这两种的形式的意义不一样,一般来说精确到哪一位可以表示误差绝对值的大小,例如精确到米,说明结果与实际数相差不超过米,而有效数字往往用来比较几个近似数哪个更精确些.一、选择题(共10题;每题2分,共20分)1.(2分)(2023七上·海曙期末)宁波文创港三期已正式开工建设,总建筑面积约,272000用科学记数法表示,正确的是( )A. B. C. D.【答案】B【规范解答】解:.故答案为:B.【思路点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.2.(2分)(2023七上·兰溪期末)计算的结果是( )A.-1 B. C. D.【答案】A【规范解答】解:故答案为:A.【思路点拨】首先利用有理数的减法法则计算出括号中式子的结果,然后利用有理数的除法法则进行计算.3.(2分)(2023七上·江北期末)实数,在数轴上的位置如图所示,下列说法一定正确的是( )A. B. C. D.【答案】D【规范解答】解:由数轴可得:,, A、,故此选项错误;B、,故此选项错误;C、,故此选项错误;D、,故此选项正确.故答案为:D. 【思路点拨】根据数轴提供的信息可得a<0<b,且,据此直接可判断B选项;根据有理数的加法法则,绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,据此可判断A选项;根据有理数的减法法则,较小的数减去较大的数,差一定为负数,据此判断C选项;根据有理数的乘法法则,异号两数相乘,积为负,据此判断D选项.4.(2分)(2023七上·宁海期末)已知有理数a,b在数轴上如图所示,则下列式子错误的是( )A. B. C. D.【答案】D【规范解答】解:根据数轴上的点所表示的数的特点得a<0<b,, ∴a+b<0,,故A、B、C选项都正确,不符合题意; 由于-a是a的相反数,数轴上表示互为相反数的两点位于原点的两侧,并且到原点的距离相等,故表示-a的点在表示b的点的右边,而数轴上的点所表示的数,右边的总是大于左边的,故-a>b,所以D选项,错误,符合题意. 故答案为:D. 【思路点拨】根据数轴上的点所表示的数的特点得a<0<b,,据此可直接判断C选项;进而根据绝对值不相等的异号两数相加,取绝对值较大的加数的符号,可判断A选项;根据异号两数相除,商为负可判断B选项;根据互为相反数的两个数在数轴上的表示方法及数轴上点所表示的数,右边的总是大于左边的可判断D选项.5.(2分)(2023七上·通川期末)如图,数轴上点M,P,N分别表示数m,m+n,n,那么原点的位置是( )A.在线段MP上 B.在线段PN上 C.在点M的左侧 D.在点N的右侧【答案】A【规范解答】解:由点M,P,N的位置可知,m<0<n,且PN<PM,∴n-(m+n)<(m+n)-m,即-m<n,∴|m|<|n|,∴m+n>0,∴原点一定在PM上,且靠近点M.故答案为:A.【思路点拨】根据数轴可得m<0<n,且PN<PM,由两点间距离公式可得PN=n-(m+n),PM=(m+n)-m,由PN
相关资料
更多









