河北专用2023七年级数学下册第五章相交线与平行线专项1利用平行线的性质求角的度数作业课件新版新人教版

这是一份河北专用2023七年级数学下册第五章相交线与平行线专项1利用平行线的性质求角的度数作业课件新版新人教版，共10页。

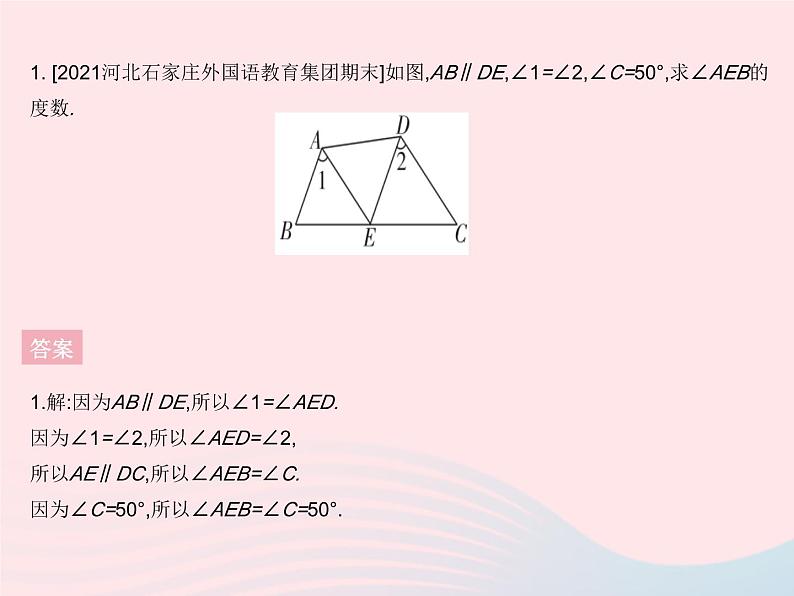
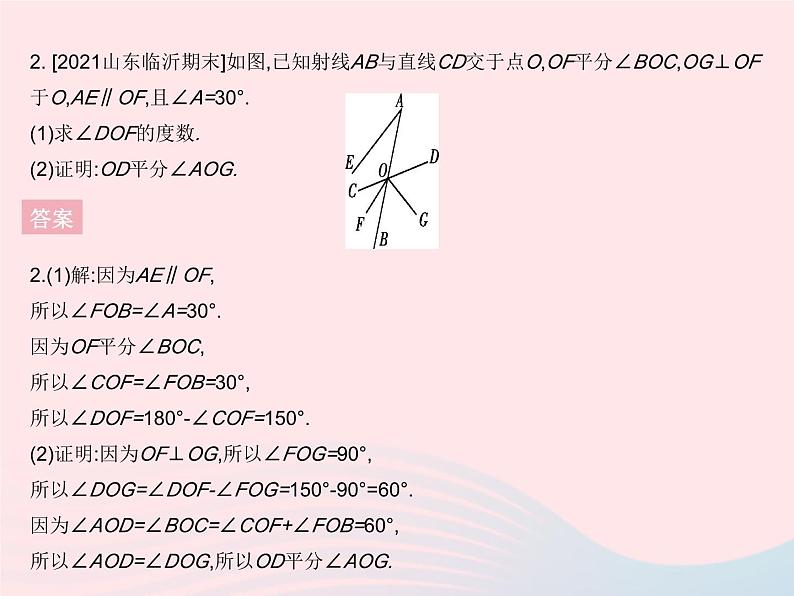
专项1　利用平行线的性质求角的度数1. [2021河北石家庄外国语教育集团期末]如图,AB∥DE,∠1=∠2,∠C=50°,求∠AEB的度数.1.解:因为AB∥DE,所以∠1=∠AED.因为∠1=∠2,所以∠AED=∠2,所以AE∥DC,所以∠AEB=∠C.因为∠C=50°,所以∠AEB=∠C=50°.答案2. [2021山东临沂期末]如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.(1)求∠DOF的度数.(2)证明:OD平分∠AOG.2.(1)解:因为AE∥OF,所以∠FOB=∠A=30°.因为OF平分∠BOC,所以∠COF=∠FOB=30°,所以∠DOF=180°-∠COF=150°.(2)证明:因为OF⊥OG,所以∠FOG=90°,所以∠DOG=∠DOF-∠FOG=150°-90°=60°.因为∠AOD=∠BOC=∠COF+∠FOB=60°,所以∠AOD=∠DOG,所以OD平分∠AOG.答案3. [2020广东广州越秀区期末]如图,已知AD∥BC,AB∥CD,点E在线段BC的延长线上,AE平分∠BAD,连接DE,∠ADC=2∠CDE,∠AED=60°.(1)求证:∠ABC=∠ADC.(2)求∠CDE的度数. 答案4. [2021重庆巴蜀中学开学考试]如图,已知AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD.(2)求∠C的度数.4.(1)证明:如图,因为AE⊥BC,FG⊥BC,所以∠CME=∠CNF=90°,所以AE∥FG,所以∠2=∠CFG.因为∠1=∠2,所以∠1=∠CFG,所以AB∥CD.答案(2)解:由(1)得AB∥CD,所以∠D+∠CBD+∠3=180°,∠C=∠3.因为∠D=∠3+60°,∠CBD=70°,所以∠3+60°+70°+∠3=180°,所以∠3=25°,所以∠C=∠3=25°.5. [2021河北沧州期中]问题情境:如图,已知AB∥CD,∠1+∠2=180°.(1)猜想论证:试猜想AD与CE的位置关系,并说明理由.(2)拓展探究:若CE⊥AE于点E,∠2= 145°,请自行给∠ABF或∠ABD一个合适的值,再求∠F的度数.5.解:(1)AD∥CE.理由如下:因为AB∥CD,所以∠1=∠ADC.因为∠1+∠2=180°,所以∠ADC+∠2=180°,所以AD∥CE.答案(2)如图,过点A作AM∥DF,因为∠1+∠2=180°,∠2=145°,所以∠1=35°.因为CE⊥AE,所以∠CEF=90°.由(1)知AD∥CE,所以∠DAF=∠CEF=90°,所以∠BAF=∠DAF-∠1=55°.因为AM∥DF,所以∠BAM=∠ABD,∠F=∠MAF,所以∠F=∠MAF=∠BAM-∠BAF=∠ABD-55°.给定∠ABD=105°,则∠F=105°-55°=50°.(答案不唯一)