2022-2023学年新疆喀什地区巴楚县九年级（上）期末数学试卷（含解析）

这是一份2022-2023学年新疆喀什地区巴楚县九年级（上）期末数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列四个名牌大学校徽图案中，是中心对称图形的是( )
A. B. C. D.
2.对于抛物线y=−3(x+1)2−2，下列说法正确的是( )
A. 抛物线开口向上B. 当x≥1时，y随x增大而减小
C. 函数最小值为−2D. 顶点坐标为(1,−2)
3.一元二次方程x2−5x+2=0的根的情况是( )
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 没有实数根D. 无法确定
4.已知，一个扇形的圆心角为60°，半径为3，则这个扇形的弧长是( )
A. 3πB. 2πC. 32πD. π
5.如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为( )
A. 10
B. 2 2
C. 3
D. 2 5
6.如图，小明和小刚分别设计了两个转盘(每一个转盘中的扇形面积均相等)，两人利用设计出的两个转盘进行“配紫色”游戏，即每人将两个转盘各转动一次，如果红色和蓝色分别出现在两个转盘上，那就说明可以配成紫色，那么小明转出紫色的概率是( )
A. 13B. 12C. 16D. 29
7.如图，⊙O的直径AB=12，CD是⊙O的弦，CD⊥AB，垂足为P，且BP：AP=1：5.则CD的长为( )
A. 2 5
B. 4 5
C. 4 2
D. 8 2
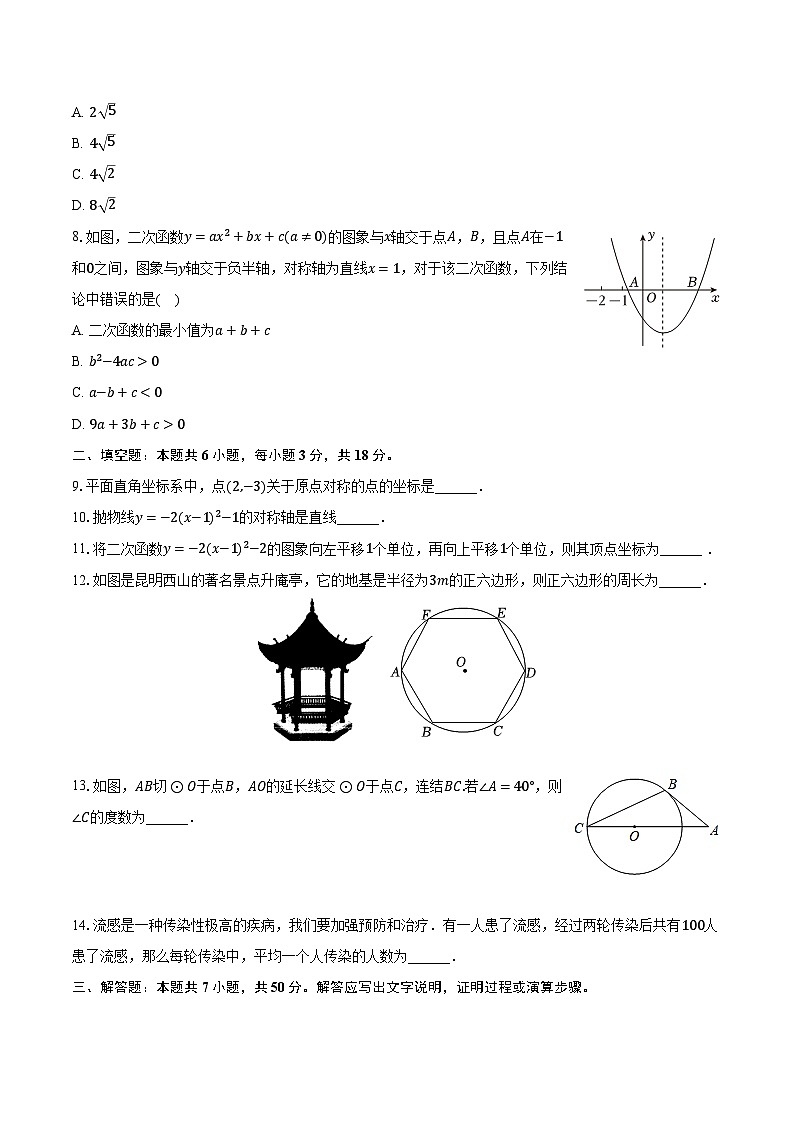
8.如图，二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A，B，且点A在−1和0之间，图象与y轴交于负半轴，对称轴为直线x=1，对于该二次函数，下列结论中错误的是( )
A. 二次函数的最小值为a+b+c
B. b2−4ac>0
C. a−b+c<0
D. 9a+3b+c>0
二、填空题：本题共6小题，每小题3分，共18分。
9.平面直角坐标系中，点(2,−3)关于原点对称的点的坐标是______．
10.抛物线y=−2(x−1)2−1的对称轴是直线______．
11.将二次函数y=−2(x−1)2−2的图象向左平移1个单位，再向上平移1个单位，则其顶点坐标为______ ．
12.如图是昆明西山的著名景点升庵亭，它的地基是半径为3m的正六边形，则正六边形的周长为______．
13.如图，AB切⊙O于点B，AO的延长线交⊙O于点C，连结BC.若∠A=40°，则∠C的度数为______．
14.流感是一种传染性极高的疾病，我们要加强预防和治疗．有一人患了流感，经过两轮传染后共有100人患了流感，那么每轮传染中，平均一个人传染的人数为______．
三、解答题：本题共7小题，共50分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题6分)
解方程：2x(x+5)=x+5．
16.(本小题6分)
在平面直角坐标系中，△ABC的三个顶点在格点上(每个方格的边长均为1个单位长度)．
(1)请画出△ABC关于原点对称的图形△A1B1C1；
(2)将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2．
17.(本小题8分)
已知二次函数y=−x2+4x．
(1)用配方法求出该函数图象的顶点坐标和对称轴．
(2)选取适当的数据填入下表，并在如图的直角坐标系内描点画出该抛物线的图象．
18.(本小题8分)
在践行“安全在我心中，你我一起行动”主题手抄报评比活动中，共设置了“交通安全、消防安全、饮食安全、防疫安全”四个主题内容，推荐子航和紫琪两名学生参加评比，若他们每人从以上四个主题内容中随机选择一个，每个主题被选择的可能性相同．
(1)子航选择交通安全手抄报的概率为______；
(2)求子航和紫琪选择同一主题手抄报的概率．(用树状图或列表法求解)
19.(本小题8分)
综合与实践
问题情境：如图1所示的是山西晋城景德桥，又名沁阳桥、西关大桥，是山西晋城市城区通往阳城、沁水的交通要道，是继赵州桥之后我国现存历史悠久的古代珍贵桥梁之一.桥拱截面OBA可以看作抛物线的一部分(如图2)，在某一时刻，桥拱内的水面宽约20米，桥拱顶点B到水面的距离为4米．
模型建立：
(1)如图2，以该时刻水面为x轴，桥拱与水面的一个交点为原点建立直角坐标系，求桥拱部分抛物线的解析式．
问题解决：
(2)求在距离水面2米处桥拱宽度．
(3)现有两宽为4米，高3米(带货物)的小舟，相向而行，恰好同时接近拱桥，问两小舟能否同时从桥下穿过，并说明理由．
20.(本小题6分)
有长为30米的篱笆，一面利用墙(墙的最大可用长度为12米)，围成中间隔有一道篱笆(平行于AB)的矩形花圃，设花圃的一边AB为x米，面积为y平方米．
(1)用含x的代数式表示y，并求出x的取值范围；
(2)如果要围成面积为63平方米的花圃，AB的长是多少？
21.(本小题8分)
如图，AB为⊙O直径，C为⊙O上一点，点D是BC的中点，DE⊥AC于E，DF⊥AB于F．
(1)求证：DE是⊙O的切线；
(2)若OF=4，求AC的长度．
答案和解析
1.【答案】C
【解析】解：A、图形不是中心对称图形，不符合题意；
B、图形不是中心对称图形，不符合题意；
C、图形是中心对称图形，符合题意；
D、图形不是中心对称图形，不符合题意．
故选：C．
根据中心对称图形的概念对各选项分析判断即可得解．
本题考查中心对称图形的概念：在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．
2.【答案】B
【解析】解：∵y=−3(x+1)2−2，
∴抛物线开口向下，对称轴为直线x=−1，顶点为(−1,−2)，函数最大值为−2，
∴当x≥−1时，y随x增大而减小，
故B选项说法正确，A、C、D选项的说法错误；
故选：B．
根据a的符号求得开口方向，根据二次函数的顶点式确定抛物线的顶点坐标，即可求解．
本题考查的是二次函数的性质，熟知二次函数的顶点式是解答此题的关键．
3.【答案】A
【解析】解：Δ=(−5)2−4×1×2=17>0，
∴有两个不相等的实数根，
故选：A．
根据判别式的值确定根的情况即可．
本题主要考查判别式与根的关系，能够熟练计算判别式并判断根的情况是解题关键．
4.【答案】D
【解析】解：根据条件得扇形弧长=60×π×3180=π．
故选：D．
利用扇形弧长公式即可解答．
本题考查扇形弧长公式，熟记弧长公式l=nπr180是解题的关键．
5.【答案】A
【解析】【分析】
题目考查勾股定理和旋转的基本性质，解决此类问题的关键是掌握旋转的基本性质，特别是线段之间的关系．题目整体较为简单，适合随堂训练．
通过勾股定理计算出AB长度，利用旋转性质求出各对应线段长度，利用勾股定理求出B、D两点间的距离．
【解答】
解：∵在△ABC中，∠C=90°，AC=4，BC=3，
∴AB=5，
∵将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，
∴AE=4，DE=3，
∴BE=1，
在Rt△BED中，
BD= BE2+DE2= 10．
故选：A．
6.【答案】C
【解析】解：列表得：
由表知，共有12种等可能结果，其中配成紫色的有2种结果，
∴能配成紫色的概率是212=16，
故选：C．
首先根据题意列出表格，然后由表格即可求得所有等可能的结果，继而得出答案．
此题考查的是用列表法或树状图法求概率．注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．
7.【答案】B
【解析】解：连接OC，
∵AB=12，BP：AP=1：5，
∴BP=2，AP=10，
∴OP=6−2=4，
∵AB⊥CD，
在Rt△COP中，由勾股定理得：
CP= OC2−OP2= 62−42=2 5，
∴由垂径定理得CD=2CP=4 5，
故选：B．
连接OC，根据题意求出OP，根据勾股定理求出CP，根据垂径定理解答即可．
本题考查的是垂径定理、勾股定理，掌握垂直于弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．
8.【答案】C
【解析】解∵根据图象可知抛物线的开口朝上，
∴抛物线有最小值，
∵对称轴为直线x=1，
∴当x=1时，函数值最小，且最小值为：y=a×12+b×1+c=a+b+c，
∴A项正确；
∵抛物线与x轴有两个交点，
∴令y=0时，可得一元二次方程ax2+bx+c=0，且此时方程有两个不相等的实数根，
∴方程的判别式Δ=b2−4ac>0，
∴故B正确；
∵由图可知：当x=−1，函数值大于0，
∴将x=−1代入抛物线解析式，
有：y=ax2+bx+c=a×(−1)2+b×(−1)+c=a−b+c>0，
∴故C项错误；
∵对称轴为直线x=1，
∴根据对称性可知x=−1时和x=3时，函数值相等，
∵当x=−1，函数值大于0，
∴当x=3，函数值大于0，
∴将x=3代入抛物线解析式，
有：y=ax2+bx+c=a×32+b×3+c=9a+3b+c>0，
∴故D项正确；
故选：C．
根据抛物线的开口方向和对称轴可判断A项；根据抛物线与x轴有两个交点，可判断B项；根据图象可知当x=−1，函数值大于0，可判断C项；根据对称性可知x=−1时和x=3时，函数值相等，即可判断D项．
本题主要考查了二次函数的图象与性质，二次函数与一元二次方程的关系的知识，掌握二次函数的图象与性质，是解答本题的关键．
9.【答案】(−2,3)
【解析】解：点P(2,−3)关于原点对称的点的坐标是(−2,3)，
故答案为：(−2,3)．
根据关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反可直接得到答案．
此题主要考查了关于原点对称的点的坐标特点，关键是掌握点的坐标的变化规律．
10.【答案】x=1
【解析】解：∵y=−2(x−1)2−1，
∴该抛物线的对称轴是直线x=1，
故答案为：x=1．
根据抛物线的顶点式，可以直接写出抛物线的对称轴．
本题考查二次函数的性质，解答本题的关键是明确题意，由顶点式可以直接写出对称轴．
11.【答案】(0,−1)
【解析】解：将二次函数y=−2(x−1)2−2的图象先向左平移1个单位，再向上平移1个单位后的解析式为y=−2(x−1+1)2−2+1=−2x2−1，
∴平移后图象的顶点坐标为(0,−1)，
故答案为：(0,−1)．
根据二次函数图象平移的规律解答．
此题考查了二次函数图象平移的规律：左加右减，上加下减，熟记规律是解题的关键．
12.【答案】18m
【解析】解：连接OC、OD，
∵六边形ABCDEF为正六边形，
∴∠COD=60°，
∵OC=OD，
∴△COD为等边三角形，
∴CD=OC=3m，
∴正六边形的周长为：3×6=18(m)，
故答案为：18m．
连接OC、OD，根据正六边形的性质求出∠COD=60°，根据等边三角形的性质求出CD，根据正六边形的周长公式计算，得到答案．
本题考查的是正多边形与圆、等边三角形的判定和性质，正确求出正六边形的中心角是解题的关键．
13.【答案】25°
【解析】解：如图，连接OB．
∵AB是⊙O切线，
∴OB⊥AB，
∴∠ABO=90°，
∵∠A=40°，
∴∠AOB=90°−∠A=50°，
∵OC=OB，
∴∠C=∠OBC，
∵∠AOB=∠C+∠OBC，
∴∠C=25°．
故答案为：25°．
连接OB，先根据切线的性质求出∠AOB，再根据OB=OC，∠AOB=∠C+∠OBC即可解决问题．
本题考查切线的性质、等腰三角形的性质、直角三角形两锐角互余等知识，解题的关键是添加辅助线构造直角三角形．
14.【答案】9人
【解析】解：设每轮传染中平均一个人传染的人数为x人，
那么由题意可知1+x+x(1+x)=100，
整理得，x2+2x−99=0，
解得x1=9，x2=−11(不符合题意，舍去)．
那么每轮传染中平均一个人传染的人数为9人．
故答案是：9人．
流感是一种传染性极高的疾病，我们要加强预防和治疗．有一人患了流感，经过两轮传染后共有100人患了流感，那么每轮传染中，平均一个人传染的人数为．
主要考查增长率问题，本题要注意的是，患流感的人把病毒传染给别人，自己仍然是患者，人数应该累加，这个问题和细胞分裂是不同的．
15.【答案】解：2x(x+5)=x+5，
变形得，2x(x+5)−(x+5)=0，
因式分解得，(x+5)(2x−1)=0，
∴x+5=0或2x−1=0，
解得x1=−5，x2=12．
【解析】变形后利用因式分解法解一元二次方程即可．
此题考查了一元二次方程，熟练掌握一元二次方程的解法是解题的关键．
16.【答案】解：(1)如图所示，△A1B1C1即为所求；
(2)如图所示，△A2B2C2即为所求．

【解析】(1)利用关于原点对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2即可．
本题考查了作图−旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
17.【答案】0 1 2 3 4 0 3 4 3 0
【解析】解：(1)∵y=−x2+4x=−(x−2)2+4，
∴该函数的顶点坐标为(2,4)，对称轴是直线x=2；
(2)由y=−x2+4x可得：
故答案为：(0,0)，(1,3)，(2,4).(3,3)，(4,0)，
函数图象如下图所示：
(1)根据配方法可以将二次函数解析式化为顶点式，然后即可写出顶点坐标和对称轴；
(2)根据题意和题目中的函数解析式，即可写出该抛物线上的五个点，然后作图即可．
本题考查二次函数的图象、二次函数的性质，解答本题的关键是会用配方法将函数解析式化为顶点式．
18.【答案】14
【解析】解：(1)子航选择交通安全手抄报的概率为14，
故答案为：14；
(2)将交通安全、消防安全、饮食安全、防疫安全分别记作A、B、C、D，
画树状图如图：
共有16种等可能的结果，两人恰好选中同一主题的结果有4种，
则两人恰好选中同一主题的概率为416=14．
(1)直接根据概率公式求解即可；
(2)画树状图，共有16种等可能的结果，两人恰好选中同一主题的结果有4种，再由概率公式求解即可．
本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
19.【答案】解：(1)由题意得，点O和点A的坐标分别为(0,0)和(20,0)，
∵B为函数顶点，
∴B(10,4)，
设抛物线解析式为y=a(x−h)2+k，
∵顶点B(10,4)，
∴y=a(x−10)2+4，
再将O(0,0)代入解析式可得，a(0−10)2+4=0，
解得a=−125，
∴抛物线的解析式为y=−125(x−10)2+4(0≤x≤20)；
(2)由题意得，令y=2可得，−125(x−10)2+4=2，
解得x1=10+5 2,x2=10−5 2，
∴桥拱宽度为：10+5 2−(10−5 2)=10 2(米)
(3)两小舟能同时从桥下穿过，理由如下：
∵两小舟的高均为3米，
∴当y=3时，−125(x−10)2+4=3，
解得x1=15，x2=5，
∴最大能通行的宽度为：15−5=10(米)，
∵两小周宽为4米，
∴10>4+4=8，
∴两小舟能同时从桥下穿过．
【解析】(1)设抛物线解析式为y=a(x−h)2+k，再根据题意求解即可；
(2)由题意得，令y=2解出方程即可得到解答；
(3)由题意得，令y=3解出方程，再进行判断即可得到解答．
本题考查了二次函数的应用，掌握二次函数的图象和性质是解决本题的关键．
20.【答案】解：(1)∵AB的长为x米，且篱笆的总长度为30米，
∴BC的长为(30−3x)米，
∴花圃的面积为：y=x(30−3x)，
∴30−3x>030−3x≤12，
解得：6≤x≤10，
∴y=x(30−3x)(6≤x≤10)；
(2)依题意得：y=x(30−3x)=63，
整理得：x2−10x+21=0，
解得：x1=3(不符合题意，舍去)，x2=7，
答：AB的长是7米．
【解析】(1)根据各边之间的关系，可得出BC的长为(30−3x)米，利用矩形的面积计算公式，可用含x的代数式表示y，再结合BC的长非负且长度不超过12米，即可得出x的取值范围；
(2)根据围成花圃的面积为63平方米，即可得出关于x的一元二次方程，解之取其符合题意的值即可得出结论．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
21.【答案】(1)证明：连接OD、AD．

∵点D是BC的中点，
∴BD=CD，
∴∠DAO=∠DAC，
∵OA=OD，
∴∠DAO=∠ODA，
∴∠DAC=∠ODA，
∴OD/​/AE，
∵DE⊥AE，
∴∠AED=90°，
∴∠AED=∠ODE=90°，
∴OD⊥DE，
∴DE是⊙O的切线．
(2)解：连接BC．

∵AB是⊙O直径，
∴∠ACB=90°，
∵OD/​/AE，
∴∠DOB=∠EAB，
∵∠DFO=∠ACB=90°，
∴△DFO∽△BCA，
∴OFAC=ODAB=12，
即4AC=12，
∴AC=8．
【解析】(1)连接OD、AD.只要证明OD/​/AE，由DE⊥AC，推出DE⊥OD即可解决问题；
(2)连接BC.只要证明△DFO∽△BCA，推出OFAC=ODAB=12即可解决问题；
本题考查切线的判定和性质、垂径定理、勾股定理、相似三角形的性质等知识，解题的关键是学会添加常用辅助线，正确寻找相似三角形解决问题，属于中考常考题型．x
…
______
______
______
______
______
…
y
…
______
______
______
______
______
…
红
黄
绿
蓝
红
红红
红黄
红绿
红蓝
蓝
蓝红
蓝黄
蓝绿
蓝蓝
白
白红
白黄
白绿
白蓝
x
…
0
1
2
3
4
…
y
…
0
3
4
3
0
…